• Contatti
  • On Air [Coming Soon]

X smartphone: non è necessario iscriversi al sito per leggere gli articoli. Scorrete verso il basso e troverete il primo.

  1. Forum
  3. Misteri
  5. Fenomeni inspiegabili
  7. Terra Piatta

Terra Piatta

15/06/2017 14:16 - 15/06/2017 14:19 #9763 da Marauder
Risposta da Marauder al topic Terra Piatta

Marauder, il punto visibile da un osservatore in un punto qualsiasi della superficie terrestre, è posto su una retta che passa per tre punti::
1) l'osservatore
2) l'orizzonte
3) il punto visibile
Tale retta, sull'orizzonte, è tangente alla superficie terrestre.

Cosa non ti torna?


A me quello torna: quello che non torna a te e Pirrone é che considerate il punto dell'orizzonte uguale alla cima dell'oggetto osservato indipendentemente dalla sua altezza.
Se alla Gorgona ci fosse un pisello alto 3000 metri, voi usereste esattamente la stessa formula, semplicemente usereste 3000 invece di 255, considerando sempre il tutto come un triangolo rettangolo che invece é indeformabile. Sono riuscito a spiegarmi o devo riformulare?
In questo caso Pirrone considera quella h come 255. Nel tuo caso era l'altro monte. quell'h é una quota fissa a partire dal basso, non la misura del punto piú alto di quello che si sta osservando.

File allegato:
You'll not see this coming.
L\'Argomento è stato bloccato.
15/06/2017 15:32 #9764 da FranZeta
Risposta da FranZeta al topic Terra Piatta
@Pirrone

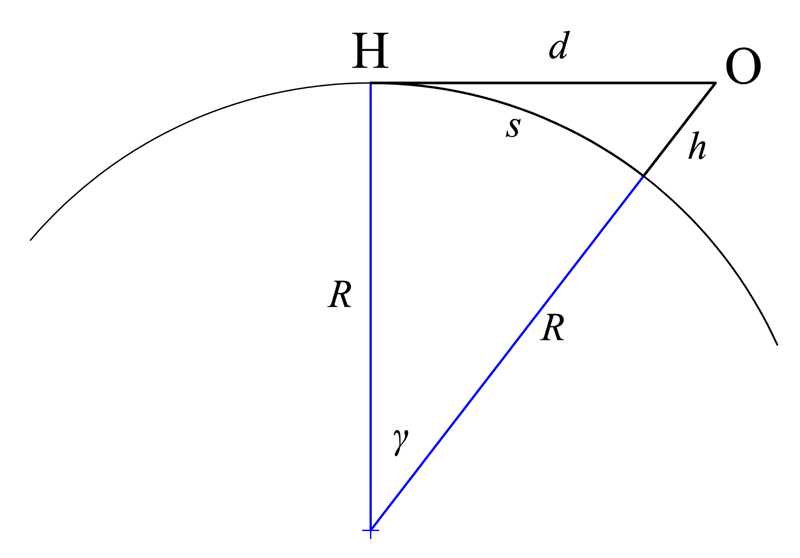
Allora con riferimento al disegno postato qui sopra da Marauder, un osservatore posto alla quota h vede l'orizzonte a una distanza d data dalla formula:
d=sqrt(2*h*r+h^2)         (1)
e questa è la formula esatta*. Siccome h è molto piccolo rispetto al raggio terrestre r si può trascurare il termine h^2 per cui si ottiene la formula semplificata:
d=sqrt(2*h*r)
 =sqrt(2*r)*sqrt(h)
 =3569.59*sqrt(h)           (2)
ed ecco da dove salta fuori la formula di wikipedia, che in effetti in questo caso è un'ottima approssimazione della formula esatta (1).

Veniamo ora al caso in cui l'osservatore sta alla quota h0 e l'oggetto osservato alla quota h1. Dubito fortemente che wikipedia suggerisca di sommare le due altezze h0+h1=h e poi inserire questa somma h nella formula (2), perchè questa è una semplificazione inutile e che comporta un grosso errore. Il procedimento corretto è calcolare le due distanze relative ad h0 e h1 con la formula (2) ( o meglio ancora con la (1)) e poi sommare queste distanze. D'altronde era già tutto spiegato nel famoso commento a pagina 5 di questo thread:

Nel caso in cui l'osservatore sia a x metri e l'oggetto osservato a y metri di quota, si sommano i valori.
Esempio: Gorgona è alta 255 metri, il monte Fasce 800, dal grafico si vede che a 250 metri corrispondono circa 55 km di distanza dell'orizzonte, a 800 poco più di 100 km, quindi in totale abbiamo circa 155 km. Questa è la distanza massima dalla quale si può osservare la sommità di Gorgona da una altezza di 800 m.

Quindi siamo parecchio lontani dai 114 km che risultano dai tuoi conti. Il mio grafico nel commento 9752 era semplicemente una quantificazione di questo errore dal confronto fra la formula esatta in blu e quella superapprossimata in rosso: le due coincidono solo se h0=0 o h1=0, negli altri casi sono parecchio lontane.

*Dimostrazione:
d^2+r^2=(r+h)^2  <------  (Pitagora)

d^2+r^2=r^2+2*h*r+h^2

d^2=2*h*r+h^2

d=sqrt(2*h*r+h^2)
FranZη
L\'Argomento è stato bloccato.
15/06/2017 15:41 #9765 da Marauder
Risposta da Marauder al topic Terra Piatta
L'immagine postata é quella che aveva linkato Pirrone in precedenza
You'll not see this coming.
L\'Argomento è stato bloccato.
15/06/2017 16:55 - 15/06/2017 17:00 #9766 da Pirrone
Risposta da Pirrone al topic Terra Piatta
Oooook ok ho capito il mio errore. Il Teorema di Pitagora calcola la distanza dell'orizzonte da un osservatore posto sul livello del mare. Se l'osservatore si alza, gli angoli si modificano e non sussiste più il triangolo rettangolo. Anche il grafico di Franzeta vale per l'osservatore posto a livello del mare (a mio avviso).
Quindi bisogna sommare la distanza dell'orizzonte dall'osservatore a quella da un ipotetico osservatore posto in cima all'oggetto osservato. Il trafiletto "oggetti sopra l'orizzonte" presente alla pagina "orizzonte " di wikipedia lo spiega, non so perchè fin'ora mi era sfuggito :question: Addiritturra vi si dice che la rifrazione atmosferica può aumentare la distanza reale dell'orizzonte fino a circa l'8% in base alle condizioni atmosferiche...

Quindi rifacendo i Calcoli per Gorgona:

altezza osservatore = h1 = 800 m
altezza oggetto osservato = h2 = 225 m
distanza dell'orizzonte rispetto all'osservatore = d1
distanza dell'orizzonte rispetto alla cima dell'oggetto osservato = d2

d1 = 3,57 sqrt h1 = 103 km
d2 = 3,57 sqrt h2 = 53 km
d totale = 156 km

La distanza tra Gorgona e Genova (un'altura nei pressi a 800 m) è di 132 km, quindi sarebbe perfettamente visibile.

Tuttavia, rimane in piedi la questione posta da Aigor relativa al Monte Cinto, perchè l'osservatore è posto sul livello del mare (Sanremo), ed è quindi applicabile il Teorema di Pitagora come giustamente lui ha fatto.
Rianalizziamo i dati:
altezza oggetto osservato = h = monte Cinto 2706
essendo h molto più piccolo del raggio terrestre, possiamo applicare la formula approssimata: d = 3,57 sqrt h = 185,70 km
La distanza effettiva tra Sanremo e il Monte Cinto è di 186,04 km. Ciò significherebbe che il Monte CInto non dovrebbe proprio vedersi (di circa 304 metri).
Tuttavia, tutto questo trascura l'effetto della rifrazione atmosferica, che secondo wikipedia può aggiungere fino all'8%. In quel trafiletto questo 8% lo aggiunge nel 3,57, che diventa così 3,86. Quindi:
d = 3,86 sqrt 2706 = 201 km
Considerando la storia dell'8% corretta, si potrebbe tranquillamente vedere anche il Monte Cinto da Sanremo.
L\'Argomento è stato bloccato.
15/06/2017 17:29 #9767 da FranZeta
Risposta da FranZeta al topic Terra Piatta

Pirrone ha scritto: Oooook ok ho capito il mio errore. Il Teorema di Pitagora calcola la distanza dell'orizzonte da un osservatore posto sul livello del mare. Se l'osservatore si alza, gli angoli si modificano e non sussiste più il triangolo rettangolo. Anche il grafico di Franzeta vale per l'osservatore posto a livello del mare (a mio avviso).

Einen moment bitte!
Un osservatore posto idealmente al livello del mare (h=0) non vedrebbe alcun orizzonte, o meglio vedrebbe un orizzonte a distanza zero. Questo si vede subito dalla formula (1) o la formula (2) del mio commento precedente. Il grafico postato a pagina 5 rappresenta la distanza dell'orizzonte per un osservatore posto alla quota h! Quello che sta a livello del mare è ovviamente l'orizzonte, non l'osservatore.

Tuttavia, rimane in piedi la questione posta da Aigor relativa al Monte Cinto, perchè l'osservatore è posto sul livello del mare (Sanremo), ed è quindi applicabile il Teorema di Pitagora come giustamente lui ha fatto.

Qui invece entra in gioco la seconda formula, più complicata, di cui discutiamo dal commento 9675 in poi, sulla base della considerazione che a livello pratico nessun osservatore è mai al livello del mare, ma almeno un paio di metri sopra. Se sei alla finestra di una casa di Sanremo sarai almeno 10 metri sul livello del mare, e quei 10 metri fanno già una bella differenza rispetto a ciò che si può vedere alla distanza della Corsica. La formula in questione vale qualunque sia l'altezza h0 dell'osservatore, non solo a Sanremo, e restituisce l'altezza minima visibile sopra l'orizzonte alla distanza d.
FranZη
L\'Argomento è stato bloccato.
15/06/2017 17:49 - 15/06/2017 23:35 #9769 da Pirrone
Risposta da Pirrone al topic Terra Piatta
Ah beh ovvio, per "osservatore al livello del mare" si intende all'altezza media dell'essere umano (diciamo 1,70 m).
Si, in effetti sarebbe meglio dire che col Teorema di Pitagora (e con il tuo grafico) si calcola la distanza dell'orizzonte per un osservatore posto ad una quota h.
Se però si vuole capire entro quale distanza un osservatore posto ad una quota h1 è in grado di vedere un oggetto di altezza h2 la faccenda si complica, e (stando a quanto scritto su wikipedia) si deve sommare la distanza dell'orizzonte relativa all'osservatore a quella relativa ad un ipotetico osservatore posto sulla punta dell'oggetto osservato.

A proposito... se è vero che da Genova (e intendo Genova città) si vede l'isola di Capraia, il che si dovrebbe dimostrare, in base a questi calcoli sarebbe impossibile e rimarrebbe soltanto il "miraggio superiore" come spiegazione...

dimostrazione:
altezza osservatore = h1 = Genova, 19 m
altezza oggetto osservato = h2 = Capraia, 52 m
d1 = 3,86 sqrt h1 = 17
d2 = 3,86 sqrt h2 = 28
d totale = 45 km
Genova e Capraia distano 167 km!
L\'Argomento è stato bloccato.
15/06/2017 23:54 #9770 da Marauder
Risposta da Marauder al topic Terra Piatta

Oooook ok ho capito il mio errore. Il Teorema di Pitagora calcola la distanza dell'orizzonte da un osservatore posto sul livello del mare. Se l'osservatore si alza, gli angoli si modificano e non sussiste più il triangolo rettangolo.

Dici correttamente ma non esattamente quello che ho detto io.
Non vorrei risultare pedante ma mi scoccia non riuscire a far capire quel che scrivo per cui faccio un ultimo tentativo.
Utilizziamo l'immagine di Wikipedia.
L'osservatore è sul livello del mare, anche se poco cambia.

L'errore che hai fatto è considerare il segmento h uguale a 255 m, ossia hai fatto coincidere la​ sommità con l'orizzonte, indicato infatti da una O.
Nel suo esempio Aigor ha fatto la stessa identica cosa ma ha considerato il segmento h alto come il monte Cinto: in pratica voi commettete la svista di considerare quello come orizzonte mentre esso si trova, foto alla mano, ben al di sotto del punto da voi indicato.
Quella O sono le parti visibili più in basso di un oggetto X ad una distanza Y. Se usassimo invece che dei monti dei grattacieli sarebbe come dire che in una determinata condizione si in grado di vedere i piani dal dodicesimo in su: se il palazzo ha 20 piani ne vedi solo 9, se ne ha 100 ne vedi 89, ma l'undicesimo non lo vedrai mai.
Quindi quel punto è il dodicesimo piano dell'esempio e non può essere contemporaneamente il 20esimo di uno è il 100esimo dell'altro.
Fatemi sapere se sta volta ci siamo, grazie.
You'll not see this coming.
L\'Argomento è stato bloccato.
16/06/2017 01:03 #9771 da FranZeta
Risposta da FranZeta al topic Terra Piatta
Ragazzi suvvia, fate i bravi, non so bene di cosa si stia parlando adesso, ma in questa immagine:

File allegato:


...in O si trova l'osservatore e in H l'orizzonte, per la miseria! Anche le lettere dovrebbero aiutare a cogliere la cosa...
FranZη
L\'Argomento è stato bloccato.
16/06/2017 07:58 #9772 da Marauder
Risposta da Marauder al topic Terra Piatta
FranZ quando scrivi "non so bene di cosa si stia parlando adesso" lo fai solo per farmi salire a 140 l'istinto omicida, vero?
You'll not see this coming.
L\'Argomento è stato bloccato.
16/06/2017 15:24 #9773 da FranZeta
Risposta da FranZeta al topic Terra Piatta

Marauder ha scritto: FranZ quando scrivi "non so bene di cosa si stia parlando adesso" lo fai solo per farmi salire a 140 l'istinto omicida, vero?

Sì e no...capisco che con l'arrivo di Pirrone sono state riesumate cose di 60 pagine fa che hanno creato una certa confusione, ma mi pare che Aigor abbia seguito col suo schema l'impostazione corretta, quindi non capisco davvero quali siano i problemi con lui...per quanto mi riguarda dal punto di vista matematico la cosa è risolta dal già citato commento 9675 in poi, tanto per ribadirlo un'ultima volta questa è la situazione con relativa formula:

File allegato:


con d=d0+d1.

PS lo schema di Aigor era più bellino, aveva messo anche la cartolina di Sanremo...

PPS per chi ama le formule semplificate anche in questo caso si possono trascurare i termini in h02 senza perdere in precisione. Però mi domando: tanto i conti li fa il computer, perchè star lì a risparmiare termini quando si hanno le formule esatte?
FranZη
L\'Argomento è stato bloccato.
16/06/2017 15:34 #9774 da Aigor
Risposta da Aigor al topic Terra Piatta
Vediamo di capirci:

Io ho sempre parlato di un punto visibile ad una certa altezza.
Cioè: in base al mio schema (che è lo stesso postato da franzeta due commenti fa), data l'altezza dell'osservatore e una distanza data io ottengo un punto visibile A UNA DATA ALTEZZA.
Vuol dire che tutto quello che è sotto quella altezza è sotto l' orizzonte, tutto ciò che è sopra quella altezza è sopra l'orizzonte quindi visibile.
Se sono a 10 m sul livello del mare a 186 km posso vedere tutto ciò che sta SOPRA i 2300 m.
Quindi la cima del monte cinto e un bel pezzo di ciò che sta sotto, fino a 2300m di altitudine
Ma se vedo ancora più sotto qualcosa non torna.

Per quanto riguarda la gorgona le misure sono:
Altitudine osservatore: 832 m (monte fasce)
Distanza gorgona dal fasce: 128 km
Minima altezza visibile: 52m
Cioè: vedo tutto quello che sta sopra 52m e se vedo la gorgona è ok perchè arriva anche a 220m
"La violenza è l'ultimo rifugio degli incapaci" (I. Asimov - Il crollo della galassia centrale)
L\'Argomento è stato bloccato.
16/06/2017 16:35 #9775 da FranZeta
Risposta da FranZeta al topic Terra Piatta
Per quanto riguarda l'articolo postato in precedenza da Aigor che afferma che da 1300 metri di quota sopra Sanremo si riesca a vedere la costa della Corsica, forse l'errore che hanno commesso è quello di scambiare il raggio col diametro terrestre, perchè in effetti in questo modo i loro conti "tornerebbero"...va da sè che sarebbe un errore madornale.
FranZη
L\'Argomento è stato bloccato.
16/06/2017 16:38 #9776 da Pirrone
Risposta da Pirrone al topic Terra Piatta

...in O si trova l'osservatore e in H l'orizzonte, per la miseria! Anche le lettere dovrebbero aiutare a cogliere la cosa...

Ok... Ma cosa vieta di considerare l'osservatore in H sul livello del mare (0 metri, sdraiato sulla spiaggia con un binocolo :wink: ) e HO come linea sotto la quale non è possibile per lui vedere nulla (coincidente con l'orizzonte)? Di conseguenza h sarebbe l'altezza minima che un oggetto dovrebbe avere per essere visto dall'osservatore in H a una distanza d, e d la distanza massima entro la quale sarebbe possibile per lo stesso vedere un oggetto di altezza h. Quindi, io usavo questa formula per sapere a quale distanza massima potesse essere visto un oggetto di altezza h, per poi raffrontarla con la distanza reale e vedere se ci "rientrava".
L'errore è che quando l'osservatore si alza, pensavo "bastasse" sommare la sua altezza a quella dell'oggetto osservato, invece non è corretto. Occorre sommare le distanze fra i 2 orizzonti, quello relativo all'osservatore e quello relativo alla cima dell'oggetto osservato (come se avesse un altro osservatore).
Anche qui, come giustamente fa presente FranZeta, non esiste un osservatore "realmente" a livello del mare, a 0 metri. Quindi per "livello del mare" andrebbe considerato implicitamente direi un paio di metri. Di conseguenza, se si vuole fare il calcolo della distanza massima entro la quale è possibile vedere un oggetto di altezza h osservando dal "livello del mare" (2 metri), bisognerebbe aggiungere "di default" 5 km (cioè la distanza dall'orizzonte per un osservatore posto a 2 metri sul livello del mare).*

L'errore che hai fatto è considerare il segmento h uguale a 255 m, ossia hai fatto coincidere la​ sommità con l'orizzonte, indicato infatti da una O.
Nel suo esempio Aigor ha fatto la stessa identica cosa ma ha considerato il segmento h alto come il monte Cinto: in pratica voi commettete la svista di considerare quello come orizzonte mentre esso si trova, foto alla mano, ben al di sotto del punto da voi indicato.

In base a quanto scritto sopra, tecnicamente non dovrebbe essere un errore (e nemmeno quello di Aigor). Ho semplicemente cercato di calcolare a quale distanza massima un osservatore posto in un altura nei pressi di Genova alta 800 m può vedere un oggetto alto 225 (non 255) m, sulla base del ragionamento fatto in precedenza.
Ovviamente sbagliavo il calcolo per il problema sopracitato.

P.S. Per far bene, occorre sapere ESATTAMENTE a che altezza ci troviamo mentre stiamo effettuando l'osservazione, oltre che ovviamente a quale altezza si trova l'oggetto osservato. Nel caso scattassimo delle foto, a che altezza si trova la fotocamera poggiata sul cavalletto (1 metro può fare la differenza).
Certo è che, come dicevo prima, se dal mare di Genova fossimo sicuri di stare ad osservare l'Isola di Capraia, in base ai calcoli (che dovrebbero essere esatti) fatti nel mio post precedente ci sarebbe poco da ragionare...
L\'Argomento è stato bloccato.
16/06/2017 17:36 #9778 da Marauder
Risposta da Marauder al topic Terra Piatta
L'errore fatto da Pirrone era lo stesso fatto da Aigor al #9565, citato proprio perché era stato risolto ("la parte sotto la zona innevata, spannometricamente")
Entrambi facevano coincidere la misura del segmento h con l'altezza dell'oggetto osservato anziché con il punto dell'oggetto visibile all'orizzonte.
Ma cosa c'è di complicato?

Se oltre l'orizzonte vedi spuntare gli ultimi 3 metri di un grattacielo alto 100 m, il segmento h misura 97m non 100, e se vuoi includere quei 3m nello schema devi prolungare quell',h di 3m oltre la O.
Dai, mi state prendendo per il culo, non ci credo che non è comprensibile
You'll not see this coming.
L\'Argomento è stato bloccato.
16/06/2017 17:40 #9779 da FranZeta
Risposta da FranZeta al topic Terra Piatta

Ok... Ma cosa vieta di considerare l'osservatore in H sul livello del mare (0 metri, sdraiato sulla spiaggia con un binocolo :wink: ) e HO come linea sotto la quale non è possibile per lui vedere nulla (coincidente con l'orizzonte)?

Nulla te lo vieta, la situazione è sempre simmetrica: se O vede H allora H vede O (anche se nello schemino di wikipedia non ci sono dubbi che in O si intenda l'osservatore). Però poi diventa complicato capire cosa succede quando alzi l'osservatore, se lo metti in H. In ogni caso l'orizzonte nei nostri schemi è sempre un punto, visto che stiamo considerando una sezione della realtà, a meno di non voler cambiare la definizione di "orizzonte".

Ma riguardo alle isole visibili da Genova, ti riferivi per caso a questa immagine?
File allegato:


Avevamo già visto che le etichette sono per forza di cose errate perchè la Gorgona non può stare alla destra dell'Elba, vista da Genova. Non è più stato stabilito cosa si vedesse in effetti in quella foto.
FranZη
L\'Argomento è stato bloccato.
16/06/2017 18:27 #9780 da Anteater
Risposta da Anteater al topic Terra Piatta
Già una cosa piatta nella rotazione si levigherebbe ma ripeto Marte sarebbe piatta e sopratutto Saturno...e la luna è piatta? Insomma a me mi inquieta veder un cavalletto ed un orizzonte + il "miraggio"...
Allucinante...si fanno pure calcoli che si vanno ad impantanare nelle variabili...
Quello che è inquietante è il non poter sorvolare i poli...poi questa ridicola gomma da masticare sotto la scarpa..butta le calzature e marcia a piedi scalzi...il Pgreco è nella stanza, quello "esoterico"..nel percettibile ed impoderabile...

Slobbysta
La speranza e la preghiera sono un chiedere...MEGLIO INVECE DARE! ...Slobbysta
L\'Argomento è stato bloccato.
16/06/2017 18:31 #9781 da Anteater
Risposta da Anteater al topic Terra Piatta
Già una cosa piatta nella rotazione si levigherebbe ma ripeto Marte sarebbe piatta e sopratutto Saturno...e la luna è piatta? Insomma a me mi inquieta veder un cavalletto ed un orizzonte + il "miraggio"...
Allucinante...si fanno pure calcoli che si vanno ad impantanare nelle variabili...
Quello che è inquietante è il non poter sorvolare i poli...poi questa ridicola gomma da masticare sotto la scarpa..butta le calzature e marcia a piedi scalzi...il Pgreco è nella stanza, quello "esoterico"..nel percettibile ed impoderabile...cammino della vita e dei propri sensi....poi chissà stiamo sognando...

Slobbysta
La speranza e la preghiera sono un chiedere...MEGLIO INVECE DARE! ...Slobbysta
L\'Argomento è stato bloccato.
16/06/2017 19:17 #9782 da FranZeta
Risposta da FranZeta al topic Terra Piatta
Saturno... sa quando verrà il suo turno.
Le variabili non temere che alla fine sono le costanti quelle che danno piattezza al mondo.
Ne craignez pas, monsieur, la tortue!
(Leibniz su Achille e la tartaruga)
Ciao Slobbysta, stavo seguendo il filo logico...
FranZη
L\'Argomento è stato bloccato.
16/06/2017 19:26 #9783 da Aigor
Risposta da Aigor al topic Terra Piatta
Si... s ci si prendesse la briga di leggere tutto, anche se è una menata, si sarebbero capite molte cose, ad esempio che avevo già considerato errata l'identificazione con etichette riportate da franzeta poco sopra.

Purtroppo non ho più avuto modo di tornare sul fasce (la vita è tiranna) e quindi non ho per ora altra documentazione che quella postata.

Ps: nella vita reale è impossibile porsi ad altezza 0 (infatto ho sposato immediatamente le correzioni di franzeta) perchè bisognerebbe mettersi in acqua con solo gli occhi che sporgono sul pelo dell'acqua.se qualcuno riesce a fare delle foto da quella posizione ne riparliamo ;-)
Altrimenti bisogna considerare, se si è in piedi sulla battigia e il mare è una tavola,, almeno la propria altezza più mezzo metro, giusto per star sicuri. Ricordiamo che il mare ha un moto ondoso, mica è una vasca da bagno... :-D
"La violenza è l'ultimo rifugio degli incapaci" (I. Asimov - Il crollo della galassia centrale)
L\'Argomento è stato bloccato.
16/06/2017 23:29 - 16/06/2017 23:30 #9784 da Pirrone
Risposta da Pirrone al topic Terra Piatta
Chiedo scudo per la confusione, non avevo voglia di leggere 60 pagine :blush:
Marauder, io ho capito (forse) quello che dici, ma fare il calcolo con h che coincide con l'altezza dell'oggetto da osservare mi serve per trovare la distanza massima entro la quale può essere visto (per un osservatore posto sul livello del mare). Praticamente è l'equivalente di calcolare la distanza dall'orizzonte per un ipotetico osservatore posto sulla cima di quell'oggetto.
FranZeta, si anche io pensavo che le "etichette" sulla foto potevano essere sbagliate, sta di fatto che se una di quelle isole dovesse essere Capraia la faccenda potrebbe risultare divertente...
La cosa andrebbe verificata con maggiore precisione.
L\'Argomento è stato bloccato.
17/06/2017 01:07 - 17/06/2017 01:14 #9785 da Marauder
Risposta da Marauder al topic Terra Piatta
Pirrone, no prob, son contento che ci si sia capiti.
L'esempio era sbagliato quando lo si riferiva ad oggetti che si erigono sopra l'orizzonte pur avendo le basi oltre. Bon, c'è voluto un po'ma alla fine ce l'abbiamo fatta, yuppi :D
You'll not see this coming.
L\'Argomento è stato bloccato.
20/06/2017 16:25 #9824 da grease
Risposta da grease al topic Terra Piatta
postimg.org/image/5ahh4imd5/

Questo mosaico di 3 immagini della Corsica sono state eseguite da un mio amico il 16 aprile del 2014 con camera monocromatica ASI 120 MM, munita di un vecchio obiettivo da ingranditore, da 3 filmati di circa un minuto ciascuno. Riprese effettuate da Sanremo a circa 62 metri di altitudine.
L\'Argomento è stato bloccato.
22/06/2017 21:23 #9853 da Nomit
Risposta da Nomit al topic Terra Piatta
Beyond Horizons - Home of the current distant sight world record
beyondhorizons.eu/2016/08/03/pic-de-fine...spard-ecrins-443-km/
L\'Argomento è stato bloccato.
30/06/2017 10:31 #9950 da SEBIN
Risposta da SEBIN al topic Terra Piatta
Grande. Anche io apprezzo l'efficacia e l'utilità di luogocomune perchè come hai detto tu poco è davvero un sito meraiglioso, fatto apposta per la discussioni di qualsiasi tipo.
SABINO LAMONACA
L\'Argomento è stato bloccato.
30/06/2017 16:39 #9958 da SEBIN
Risposta da SEBIN al topic Terra Piatta
Perfetto. Grazie. Terrò a mente questa tua osservazione. Mi ha interessato moltissimo, lo ammetto.
SABINO LAMONACA
L\'Argomento è stato bloccato.
18/08/2017 11:40 #10471 da artemis
Risposta da artemis al topic Terra Piatta
Non so se questo sito ti sia già stato indicato come fonte abbastanza attendibile per chiarirsi parecchi dubbi. Purtroppo sono arrivata tardi in questa discussione e non è palesemente possibile per me ripercorrere tutti i post.
In genere consiglio questa lettura a chiunque abbia dubbi e perplessità:
flatearthdelusion.blogspot.it/p/calcolat...izzonte.html?fref=gc
L\'Argomento è stato bloccato.
23/08/2017 17:45 - 23/08/2017 22:18 #10491 da DanieleSpace
Risposta da DanieleSpace al topic Terra Piatta
Buongiorno,
scusate sono nuovo su questo sito dai contenuti molto interessanti.
Da tempo seguo con interesse questa curiosa "novità" della Terra piatta. Non ho potuto leggere tutte le 60 mila risposte ma ho visto calcoli trigonometrici, trattati di fisica e quant'altro. Non so se quello che sto per scrivere sia già stato scritto...
Il mio parere a riguardo è molto semplice: È PROPAGANDA. O meglio, questa teoria trova soprendente risonanza e viene usata sapientemente come arma dai debunkers.
Come funziona ?
Si crea una teoria fasulla e sciocca, facilmente smentibile e la si diffonde come "teoria alternativa". In questo modo nel pubblico si crea l'associazione inconscia "teorie alternative = sciocchezze " e "complottisti = imbecilli".
Come viene usata ?
Il passo successivo sta nel chiamare "terrapiattista" chiunque sollevi teorie scomode onde screditarlo.
Poi si fa notare che chi crede in una delle teorie del complotto, crede inevitabilmente anche nella Terra piatta, sempre per screditarlo. Insomma mettere tutto nell'immenso calderone delle cretinate. Se qualcosa è in quel calderone --> è una cretinata.
Il termine "terrapiattista" s'incontra sempre più spesso laddove c'è il dibattito su un tema controverso. Inoltre, ogni paese ha le sue, gli anglosassoni usano spesso "tinfoil hat", rimandando a dei paranoici che per non farsi leggere nella mente, coprivano il capo con questi cappelli di carta stagnola.

Non ho ancora compreso completamente questi meccanismi di transfer-propaganda ma mi rendo conto che i siti tematici in italiano ne sono pieni. Ho trovato di recente un tizio che ha fatto un video di 48 minuti in cui spiega per filo e per segno perchè questa teoria sia sbagliata, non mancando mai di ridicolizzare e di insultarne i presunti sostenitori.
Il video è su Youtube e s'intitola "TERRA PIATTA: La TEORIA della PAZZIA Documentario completo".
Guardate la durata del video e la qualità delle animazioni. Chi diavolo è che investirebbe così tanto per affermare una cosa così ovvia ?
Per ora, gli unici che ho incontrato che parlano ripetutamente di questa idea sono proprio i debunkers.
In vita mia non ho mai incontrato un conoscente o un collega che credesse in questa teoria. E voi ? :question:
Una teoria del complotto è ridicola solo quando sono ridicoli i suoi moventi.
Ringraziano per il messaggio: Sertes
L\'Argomento è stato bloccato.
23/08/2017 18:51 #10492 da joseph grease
Risposta da joseph grease al topic Terra Piatta
Sei nuovo per questo sito, ma vedo che hai tratto in un attimo le (tue conclusioni). Grazie. E poi? Tutto qui? Noi sessantamila quesiti e tu? Se fossi arrivato prima ci avresti tolto una fatica. Chiaro e limpido, il tuo discorso non fa una piega.
L\'Argomento è stato bloccato.
23/08/2017 22:30 #10494 da DanieleSpace
Risposta da DanieleSpace al topic Terra Piatta
Ciao Joseph. Io non intendo sminuire nessuno di quelli che hanno dibattuto qui dentro. Mi pareva un po' assurdo dove stava andando questa discussione...ho visto formule trigonometriche, citazioni filosofiche e altro...Ho semplicemente voluto esporre il mio ragionamento, come avete fatto voi altri. Quando mi chiedi "e poi ? ", cosa vuoi sapere, cosa vuoi che ti dica ? Tu cosa ne pensi del tema ?
Una teoria del complotto è ridicola solo quando sono ridicoli i suoi moventi.
Ringraziano per il messaggio: Sertes
L\'Argomento è stato bloccato.
24/08/2017 02:47 #10495 da FranZeta
Risposta da FranZeta al topic Terra Piatta
Visto che terrapiatta sembra avere ripreso vita, dico anche io la mia: il messaggio di artemis ha una sola, grande, pecca: essere stato postato alla pagina 66 di questo thread.

@DanieleSpace
Ho capito che ce l'hai con la trigonometria, ma se vuoi farne a meno come dimostri che la terra è tonda senza ricorrere a immagini satellitari o cose simili (escluse a priori dal discorso per gentile concessione dei tarrapallisti)? Hai presente la storia di Eratostene? Un pochetto di trigonometria serve.
FranZη
L\'Argomento è stato bloccato.
  1. Forum
  3. Misteri
  5. Fenomeni inspiegabili
  7. Terra Piatta
  • Follow Us:
Copyright @ 2019 Luogocomune. All Rights Reserved. Powered by / Redazione / Dusty / 1K8 / Luogocomune