La formula del latte è Vacca2O
mi sembra di non essermi spiegato perché, per me, non è questione di terminologia né di rifiutare questo o quell'ente matematico ma di constatare che la matematica usa il termine infinito a proposito di entità qualsivoglia la cui definizione è diversa dal significato senza limite alcuno. Tale constatazione non impegna nessuno a rinunciare alla terminologia preferita mentre chiarisce il qui pro quo dal momento che il termine infinito, nell'uso ricco di molti significati, quello matematico incluso, etimologicamente riflette con precisione il significato di senza limite alcuno che in matematica (e nel senso comune) manca (per ragioni che potrebbero ben essere generalmente condivisibili). Tantomeno detta constatazione impegna ad accettare come reale, utile, o altro il significato senza limite alcuno che, a venticinque secoli di vuota distanza, voglio riaffermare.
Esemplificando, imaginiamo un Comune che, con regolare delibera, abbia cambiato il termine divieto con permesso. I malcapitati automobilisti in sosta potranno difendersi davanti al giudice di pace perché conoscono il significato di permesso diversamente dagli altri che, orbi del significato senza limite alcuno, erroneamente accetteranno come non-finitezza l'assenza di limiti eccetto almeno uno.
Infatti, a lume di naso, qualunque ente la matematica assuma, tale ente almeno un limite pur l'avrà, o mi sbaglio ?
Riporto all'attenzione la risposta :
Mah, già qui non sono d'accordo, perchè per esempio una definizione di insieme infinito è questa: [...] che non fa nessun riferimento agli insiemi numerici. Possiamo anche ignorare l'esistenza dei numeri naturali, eppure non avremmo difficoltà ad applicare la definizione, che richiede solo i concetti di insieme, sottoinsieme e relazione biunivoca. Spesso, forse un po' semplicisticamente, si definisce la matematica come la scienza che studia le relazioni astratte fra insiemi, quindi se non accettiamo gli enti necessari alla definizione qui sopra non accettiamo la matematica tout court.
milvalos
[mlv do15ap18 15e27]
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
I limiti matematici sono sempre relativi a qualcos'altro, non esiste nulla che assomigli all'infinito "senza limite alcuno". Ma non è nemmeno detto che tale concetto abbia senso, sia pure a livello metafisico. Potrebbe per esempio coincidere con Dio, e non mi riferisco al dio cristiano o agli dei pagani, ma all'intelligenza da cui tutto ha origine. La quale, volendo essere onesti, potrebbe anche non esistere.milvalos ha scritto: Infatti, a lume di naso, qualunque ente la matematica assuma, tale ente almeno un limite pur l'avrà, o mi sbaglio ?
Tornando alla matematica: l'intervallo (0,1) è limitato? Certamente sì. E' insiemisticamente finito? Certamente no. Una retta geometrica è limitata? Certamente no. Insiemisticamente è più grande dell'intervallo di cui prima? Assolutamente no. In matematica il termine infinito può avere svariati significati a seconda del contesto, ma questi significati comprendono sempre un "senza limite alcuno" rispetto a qualcosa. "Senza limite alcuno" rispetto a tutto non è una definizione matematica accettabile, e secondo me anche dal punto di vista metafisico lascia parecchio a desiderare. Per dargli un senso dovresti prima definirmi cos'è "tutto", e ci sono fondati sospetti per pensare che questo tutto costituisca proprio l'infinito che vorremmo definire. Tra l'altro quando si considerano insiemi troppo "grandi" all'interno della logica formale iniziano a saltare fuori paradossi, questo porta alla distinzione fra "insieme" e "classe", il primo può essere considerato come elemento di un nuovo insieme, la seconda no.
Un esempio di classe propria è "l'insieme di tutti gli insiemi". In che rapporto si porrebbe questa classe rispetto all'Infinito (d'ora in poi coerentemente col mio pensiero inizio a scriverlo con la maiuscola)? E' più grande o più piccola? Da un lato dovrebbe essere più piccola, visto che l'Infinito è uno solo ed è l'unico ente immaginabile senza limite alcuno (sto ovviamente facendo mio il pensiero di Guénon), d'altra parte cosa mi impedisce di concepire la contrapposizione fra Infinito e Nulla? Bene, allora posso concepire un insieme che consta di due elementi: l'Infinito e l'insieme vuoto. Questo insieme appartiene alla classe di tutti gli insiemi, che quindi risulterebbe "più grande" dell'Infinito.
Da questi discorsi non se ne esce più, per questo preferisco restare nel terreno matematico. Una volta poste le definizioni non c'è più alcun dubbio sull'ente matematico considerato, questa è la prerogativa della matematica stessa. Poi uno può non accettare l'esistenza dell'infinito attuale, anche solo a livello astratto, e considerare solo l'infinito potenziale. Questa è la posizione degli antichi, ma anche di molti illustri moderni, da Cantor in poi questa visione epistemologica passa sotto il nome di intuizionismo. Va anche detto che l'intuizionismo, se perseguito fino alle estreme conseguenze, comporta la rinuncia al principio del terzo escluso, e con ciò non si perde solo la teoria degli insiemi di Cantor, ma gran parte della matematica conosciuta.
FranZη
Si prega Accesso a partecipare alla conversazione.
col rispondermi
I limiti matematici sono sempre relativi a qualcos'altro, non esiste nulla che assomigli all'infinito "senza limite alcuno".
riconosci, com'è del tutto ovvio anche ai non matematici, che la matematica (come qualunque espressione del comune buon senso e delle sue varie estensioni) si occupa di enti ciascuno dei quali almeno un limite non può non averlo, per esempio, il limite di essere proprio quell'ente e non un altro.
Imagino, con ciò, che concordi che attribuire infinitezza ad un ente infinito solo in parte, per esempi lo spazio e il numero, non sia il massimo della terminologica accuratezza; difetto peraltro giustificabile con l'uso e questo, almeno per me, spiegabile con la vacatio infiniti inaugurata da Anassimene e terminata, per quanto credo di saperne, il secolo scorso da Guénon nel modo per me inaccettabile sul quale sorvolo.
Possiamo perciò entrare nel nocciolo del tema del senza limite alcuno del quale affermi:
Ma non è nemmeno detto che tale concetto abbia senso, sia pure a livello metafisico.
Come previsto, dissento in base allo stesso argomento di Anassimandro il quale, con parole mie, sostiene che un proposto fondamento del cambiamento è insufficiente se ha sia pure un solo limite per il fatto che quel limite, invece di permettere lo scambio tra i limiti di cui il cambiamento è costituito, con gli stessi confliggerebbe. Il pensiero di Anassimandro ci è pervenuto di seconda e di terza mano. Le reliquie, con traduzione parallela, sono accessibili a
ancientsource.daphnet.org/
più precisamente a
ancientsource.daphnet.org/agora_show_tra...cription%3Fid%3D3407
dove si legge
λέγει γοῦν διότι ἀπέραντόν ἐστιν, ἵνα μηδὲν ἐλλείπηι ἡ γένεσις ἡ ὑφισταμένη.
e, a fronte,
E dice che è illimitato perché non venga meno la generazione che ne consegue.
Traduzione per me errata nel termine generazione (γένεσις) che invece traduco con cambiamento perché qui la teologia e la biologia non c'entrano un bel nulla mentre il mio traducente è attestato dal Rocci in Platone, sia pure indirettamente, divenire, termine fuorviante perché supponentemente predica l'idea di provenienza, tutta da dimostrare. In realtà constatiamo il cambiamento e nulla altro.
INOLTRE
il senza limite alcuno, pur, ovviamente, non avendo alcun senso (senso, infatti, chiama limite) è importante non solo a quello che chiamo il grado più astratto del pensiero (GAP) ma anche a qualunque altro perché liquefa la fissazione identitaria prima animalmente / neurologicamente, poi umanamente / culturalmente inevitabile.
milvalos
[mlv lu16ap18 22e51]
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Ovvero Berkeley vince il primo set, Leibniz poi vince il match quando è nella tomba da due secoli
Dopo un po' di filosofia tornerei alla matematica pura, con il già promesso discorso sul calcolo infinitesimale. Siccome l'argomento sarebbe davvero vasto ho messo "parte prima" (così arriva prima, direbbe il Bergonzoni...) più che altro per dare l'impressione che tutto quello che non dico qui potrà essere affrontato più avanti, ma non è affatto detto che ci sarà una parte seconda. Dunque sistemiamoci bene sulla sedia e buttiamoci a bomba sul calcolo infinitesimale.
Iniziamo subito col dire che il calcolo infinitesimale (d'ora in poi CI) è la base di quella vasta disciplina matematica nota come Analisi, tanto che in inglese si parla di calculus tout court per riferirsi al CI. A sua volta il CI si può dividere in due discipline fondanti, il calcolo differenziale e il calcolo integrale. Due definizioni piuttosto rozze ma buone per i nostri scopi di queste discipline sono:
calcolo differenziale <----> trovare la tangente (in un punto) ad una curva
calcolo integrale <---> trovare l'area racchiusa in una curva
Entrambi trovano prodromi nella geometria antica, ma solo il calcolo integrale fu sviluppato in modo simile a quello moderno, ovviamente dai greci, in particolare Archimede fu il campione massimo della disciplina. Oltre al famoso trattato Della sfera e del cilindro, a lui si devono tutta una messe di altri risultati che coinvolgono aree e baricentri di figure curve, e fino a tempi relativamente recenti non si sapeva nemmeno bene come avesse fatto a trovare tali risultati. Poi agli inizi del '900 si scoprì un palinsesto contenente un suo trattato perduto, il Metodo, e a quel punto fu chiaro che Archimede avrebbe potuto tranquillamente scrivere un moderno testo di Analisi Matematica, almeno per quanto riguarda la parte integrale.
Vediamo un esempio di "integrazione" all'antica: il calcolo dell'area del cerchio. I greci, sfruttando la loro conoscenza dei poligoni regolari, notavano che indipendentemente dal numero dei lati, l'area di questi aveva sempre la stessa espressione:
A=a*P
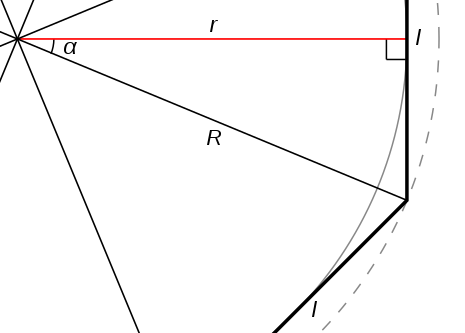
Dove a è l' apotema e P il semiperimetro (è un facile esercizio dimostrare questa formula, guardate un po' l'immagine seguente:
tenendo conto che l'apotema è indicato con r).
Siccome più aumentiamo il numero di lati di un poligono regolare più questo si avvicina alla circonferenza circoscritta (e questa a sua volta si avvicina a quella inscritta), possiamo concludere che la formula resta valida anche per la circonferenza, che in tal modo viene vista come un poligono regolare con infiniti lati (primo infinito!). Dato che l'apotema diventa il raggio del cerchio e il semiperimetro la semicirconferenza, ecco che a*P ---> r*(π*r)=πr2, e abbiamo la nota formula dell'area del cerchio. A dirla tutta i greci avrebbero lasciato indicato π come il rapporto fra circonferenza e diametro, dato che ai loro tempi il problema della "quadratura del cerchio" era ancora più che mai aperto.
Questo modo di ragionare, che viene anche detto metodo di esaustione, è sostanzialmente lo stesso che si usa nel calcolo integrale moderno, con la differenza che oggi sappiamo definire rigorosamente il concetto di passaggio al limite, cioè quel balzo che dal finito ci porta all'infinito (secondo infinito!). In realtà il concetto classico di limite non ricorre all'infinito attuale, ma solo a quello potenziale (terzo+quarto infinito!), quindi non serve riprendere da capo le discussioni fatte sopra, però come vedremo fra poco il modo di ragionare dei primordi del calcolo differenziale era ben diverso, e molto più simile a quella variante del CI che passa sotto il nome di Analisi non standard.
Ma andiamo per gradi. Come già detto il calcolo differenziale è l'altra metà del CI, il rapporto fra questo e il calcolo integrale si chiarisce solo nel 1600 quando, diversi matematici fra i quali spicca l'allievo di Galileo Evangelista Torricelli (quello del barometro), scoprono quello che oggi è noto come Teorema fondamentale del calcolo integrale, che è talmente semplice che intanto lo riporto e poi magari più tardi lo spiego:
La derivata della funzione integrale è la funzione integranda.
Al di là della terminologia, il teorema afferma semplicemente che calcolo differenziale e integrale sono uno l'inverso dell'altro, e la cosa è piuttosto sorprendente se consideriamo il significato originario delle due operazioni associate ad essi (derivazione = trovare la tangente, integrazione = trovare l'area). Con questo risultato in tasca, e con la giusta dose di genio puro e cristallino, sul finire del secolo XVII Newton e Leibniz, indipendentemente e quasi contemporaneamente, scoprono i principi del calcolo differenziale. Va anche detto che entrambi si erano basati sul metodo utilizzato da Fermat per trovare le tangenti. Insomma, qui sono coinvolti pezzi da 90 della storia della matematica.
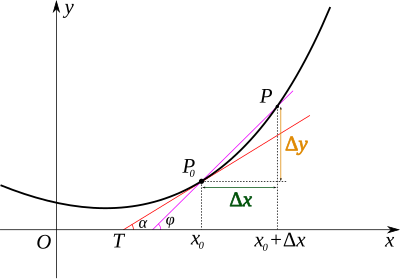
Vediamo subito come funziona questo calcolo differenziale, senza nessun preambolo, anche perchè ce ne sarebbero parecchi da fare e li trovate già tutti in un qualunque testo di Analisi 1. Mettiamo un disegnino per aiutarci:
Mi serve intanto ricordare che l'equazione di una retta passante per il punto (x0,y0) del piano cartesiano è la seguente:
y-y0=m*(x-x0)
La "m" che compare nell'equazione, detta coefficiente angolare, è il rapporto Δy/Δx delle quantità il cui significato è spiegato dalla figura. Ora ci occuperemo solo di funzioni (continue) y=f(x), il grafico della funzione è in generale una curva e il nostro intento è trovare la tangente alla curva in un suo qualsiasi punto P0=(x0,y0). L'idea è che se prendiamo la retta passante per P0 e un altro punto P sul grafico della funzione, questa si avvicinerà tanto più alla tangente quanto più P si avvicina a P0:
Siccome P0 sappiamo a priori che punto sia, l'unica cosa che ci serve per individuare la retta tangente è il coefficiente angolare "m", cioè il rapporto Δy/Δx quando queste quantità tendono a zero. A questo punto seguiamo Leibniz che ci dice: in luogo di Δx e Δy consideriamo le nuove quantità infinitesime (quinto infinito!) dx e dy, che hanno grossomodo lo stesso significato dei "lati della circonferenza" quando vediamo quest'ultima come un poligono regolare con infiniti lati, e facciamo il rapporto:
df(x0)/dx= (f(x0+dx)-f(x0))/dx
Notiamo che se prendiamo Δx invece di dx il rapporto qui sopra è precisamente Δy/Δx. Questo rapporto, se esiste, è il coefficiente angolare della retta tangente alla funzione f punto x0 (cioè al grafico di f nel punto P0). Dato che x0 è un punto generico, possiamo anche omettere l'indice e scrivere semplicemente:
(1) df(x)/dx=(f(x+dx)-f(x))/dx
che ci fornisce una nuova funzione, f'(x)=df(x)/dx, detta derivata di f, la quale punto per punto ci dà il coefficiente angolare della retta tangente ad f. NOTA LINGUISTICA: dx,dy, ecc. si leggono “de-x, de-y “, con pronuncia tedesca, mentre i rapporti dy/dx, df/dx ecc. si leggono “de-y-in-de-x, de-f-in de-x” e non “de-y-su-de-x,…” come se fosse un normale rapporto. Ciò avrà senso (se sarò bravo a spiegarmi) più avanti.
La cosa, vista così, può lasciare molto perplessi, però funziona! Facciamo un esempio pratico, prendiamo f(x)=x2 e scriviamo il rapporto (1) corrispondente a questa funzione:
((x+dx)2-x2)/dx = (x2+2xdx+dx2-x2)/dx = 2x+dx
Ci ritroviamo quindi con l'espressione 2x+dx, ma siccome dx è un infinitesimo, cioè è "più piccolo di qualsiasi numero", facciamo semplicemente finta che non ci sia e otteniamo:
(x2)’=2x
L'apostrofo dopo la funzione è un'altra notazione per df/dx e si legge "f primo". Potete controllare, o fidarvi sulla parola, ma in effetti se calcolate il coefficiente angolare della retta tangente a y=x2 (il cui grafico è una parabola) in un qualsiasi punto x, troverete che è proprio 2x. Proviamo con f(x)=x3:
((x+dx)3-x2)/dx =(x3+3x2dx+3xdx2+dx3-x3)/dx=3x2+3xdx+dx2
Anche qui, ignorando I termini che contengono dx e sue potenze, resta solo 3x2. Abbiamo dunque:
(x3)’=3x2
Non è difficile dimostrare che in generale per i monomi vale:
(2) (xn)’=nxn-1
Così come è immediato vedere che la derivata di una somma è la somma delle derivate. La formula (2) è ben più utile di quanto possa apparire, visto che ogni funzione analitica (sono le comuni funzioni che "hanno un nome", come l'esponenziale, il logaritmo, le funzioni trigonometriche, ecc.) può essere scritta in forma di serie di potenze, a questo punto si può derivare semplicemente derivando ogni termine, e i singoli termini sono proprio monomi. Prendiamo la funzione esponenziale f(x)=ex e calcoliamone il rapporto incrementale dato dalla (1):
(e(x+dx)-ex)/dx=(exedx-ex)/dx=ex ( (edx-1)/dx) =ex
Il risultato segue dal fatto che il termine nella parentesi più grossa nella penultima uguaglianza è un limite notevole, che si dimostra essere uguale a 1. Quindi la derivazione lascia invariata la funzione esponenziale, e di conseguenza vale lo stesso anche per l'integrazione. Si tratta dell'unica funzione che gode di tale proprietà. Tempo addietro (post #10628) avevamo già incontrato l'espressione della funzione esponenziale come serie di potenze:
ex=Σ N xn/n!=1+x+x2/2+x3/(2*3)+x4/(2*3*4)...
Se proviamo a derivare termine a termine questa serie, usando la formula (2) e il fatto che la derivata di una somma è la somma delle derivate, abbiamo:
d(ex)/dx=0+1+x+x2/2+...=ex
...cioè lo stesso risultato ricavato sopra, e ciò è cosa buona e giusta. Il primo termine del membro centrale è 0 per via del fatto che la derivata di un numero (ossia di una funzione costante) è sempre 0, come si può facilmente verificare sostituendo una costante alla f(x) della formula (1). La proprietà della funzione esponenziale di restare invariata per derivazione/integrazione è cruciale non solo nell'ambito dell'Analisi matematica, ma anche nella Fisica e nell'Ingegneria, per la ragione che vado ad esporvi. Potrebbe lasciare perplessi tutta questa voglia di scoprire la tangente ad una curva, cioè, ad un certo punto, ma chissenefrega...E invece no! Ce ne frega eccome, infatti prendiamo la traiettoria di un punto che si muove nello spazio, anzi, facciamo in un piano per semplificare un po', tanto i concetti sono gli stessi. Sia allora:
s(t)=(x(t),y(t))
la legge oraria del punto, cioè la funzione che, istante "t" per istante, ci dà le coordinate cartesiane x(t) e y(t) del punto. Fatto salvo per il nome diverso delle variabili indipendenti e dipendenti, siamo nella stessa situazione di prima, solo che adesso quella che chiamavamo "x" è diventata il tempo "t", e quella che era f sono le coordinate x e y espresse come funzioni del tempo. In definitiva possiamo ancora pensare di derivare queste funzioni, rispetto a "t" stavolta, ottenendo le due nuove funzioni:
x'(t)=dx(t)/dt
y'(t)=dy(t)/dt
Ora, dato che s(t) era la posizione istante per istante del punto in movimento, qual è il significato fisico della nuova funzione s'(t)=(x'(t),y'(t)) ottenuta per derivazione?
Siete pronti? Pronti pronti (quelli che lo sanno non suggeriscano...)?
E' la velocità istantanea!
Ecco che inizia un po' a chiarirsi l'importanza, anche pratica, della derivazione e del CI in generale.
Ma c'è dell'altro. Ripetiamo l'operazione di derivazione sulle coordinate di s'(t), che come appena visto ci dà la velocità del punto istante per istante, questa volta avremo:
x''(t)=d2x(t)/dt2
y''(t)=d2y(t)/dt2
Quella che ho appena usato è la notazione standard che indica la derivata seconda rispetto a "t", cioè la derivata della derivata. Chiediamoci allora: qual è il significato fisico di s''(t)=(x''(t),y''(t))?
Quella che abbiamo appena trovato signori è l'accelerazione istantanea.
Siccome tutta la fisica classica discende dalle tre leggi di Newton, la seconda delle quali vi ricordo è F=ma, la forza è il prodotto di massa e accelerazione, ora abbiamo gli strumenti per capire che questa equazione in realtà va considerata "ribaltata", ossia:
a=F/m ---> (3) d2s(t)/dt2=F(t)/m
Quello che sta scritto sopra è che se conosco la forza F(t) agente, istante per istante, su un punto materiale di massa m, per calcolare la traiettoria del moto del punto devo risolvere l'equazione (3), che coinvolge una doppia derivazione. Le equazioni di questo tipo sono le famose equazioni differenziali e saltano fuori praticamente dappertutto nelle applicazioni scientifico-tecniche. Ogni grandezza fisica è legata da integrazione o derivazione a qualche altra grandezza, e qui sta l'importanza della funzione esponenziale, che compare in molte soluzioni esplicite di equazioni differenziali, a motivo della sua proprietà di invarianza.
L'interpretazione fisica del CI è alla base dell'approccio di Newton al problema, tanto che in effetti quelle che noi definiamo funzioni erano per lui "flussioni", cioè delle quantità che variano nel tempo. Anche la sua notazione era diversa da quella scelta da Leibniz, mentre la seconda è stata in seguito adottata dall'Analisi e dalle applicazioni matematiche in generale, la prima è sopravvissuta come conveniente notazione per problemi di Fisica.
Veniamo ora ai problemi legati ai fondamenti del CI, così giustifico anche il sottotitolo del post. Come già segnalato di sfuggita, il procedimento legato all'equazione (1), anche se nella pratica funziona, nella teoria lascia parecchi dubbi. Qui salta fuori il vescovo George Berkeley e la sua critica al CI. Riportiamo il primo esempio di derivazione fatto sopra:
((x+dx)2-x2)/dx = (x2+2xdx+dx2-x2)/dx = 2x+dx
Il risultato, dice Berkeley, non è 2x, ma 2x+dx. Ora Leibniz ci dice di far finta che il dx non ci sia, dato che è un infinitesimo. C'è però un problemuccio: già dai tempi di Eudosso di Cnido si sa che non esiste nessun numero r tale che 0 < r < 1/n per ogni numero naturale n. Detto altrimenti, l'unico numero (non negativo) che sia minore di 1/n per ogni n è proprio -e solo- lo zero. Quindi il procedimento di derivazione consiste nel prendere una quantità dx, considerarla prima diversa da zero (le prime due uguaglianze), e poi porla uguale a zero (il dx che scompare dal risultato). Insomma, dx=0 sì o no? In entrambi i casi il risultato "2x" della derivazione è logicamente inconsistente.
Leibniz sapeva bene che tecnicamente Berkeley aveva ragione, ma il suo intuito gli suggeriva che il metodo era corretto, era se mai la nostra concezione dei numeri ad essere incerta. In effetti non aveva tutti i torti, dato che la teoria dei numeri reali arriverà solo un paio di secoli dopo, però per l'appunto c'era già la teoria dei rapporti di Eudosso, insomma, non è che nel primo '700 il concetto di numero fosse sconosciuto. Comunque in definitiva Leibniz suggeriva che questi infinitesimi -dx,dy eccetera- fossero delle entità a metà fra numero e non-numero, nel senso che non aveva idea di come si potesse definirle in un modo logicamente consistente, e però credeva nella loro esistenza come enti matematici. Nel frattempo Berkeley lo spernacchiava, con la logica (momentaneamente) dalla sua parte.
Nonostante l’inconsistenza logica, il CI si dimostrò da subito così straordinariamente potente da lasciarsi subito alle spalle ogni obiezione formale à la Berkeley, tanto che nell’arco di un secolo si era così sviluppato da raggiungere ogni campo delle scienze esatte. Solo nel corso dell’800 iniziò a sentirsi sempre più pressante un bisogno di sistemazione dei fondamenti, per la verità non solo del CI ma piuttosto dell’intera matematica, per quanto riguarda però il nostro ambito si trovò una soluzione grazie alla formalizzazione del concetto di limite. Sorvolerei sull’argomento, dato che pure questo fa parte del bagaglio comune ad ogni testo di Analisi, dirò solo che questa sistemazione tradisce lo spirito dello sviluppo impetuoso dell’Analisi, che è poi quello delle origini di Leibniz.
In particolare il rapporto dy/dx espresso dalla (1), in questo approccio, non è da considerarsi come un rapporto, ma una comoda scrittura che va presa come un tutt’uno, cioè un “d/dx” da applicare a una funzione “y”. Questo è un punto su cui si usa insistere molto, e chi ha studiato analisi dovrebbe averne parecchi ricordi, perché il fatto è che quasi sempre questo caveat sembra senza altro scopo che confondere le idee allo studente, dato che le cose funzionano benissimo considerando dy/dx come un vero e proprio rapporto. E’ anche opinione comune di molti storici della matematica che se questa sistemazione logica del CI fosse stata raggiunta prima, probabilmente lo sviluppo del calcolo stesso ne sarebbe stato fortemente influenzato in negativo.
Ecco però che verso la fine della nostra storia avviene un colpo di scena. Tutto nasce da arcani risultati della logica formale degli anni ’30, quando l’Analisi matematica aveva già definitivamente l’impostazione che si studia anche oggi nei corsi universitari. Ci si accorse infatti che, a partire dagli assiomi che definivano i numeri reali, era possibile costruire un altro insieme numerico ben più vasto ed enigmatico. Questo insieme, che oggi chiamiamo insieme dei numeri iperreali (indicato con *R), oltre ad avere le stesse proprietà dei numeri reali, e a contenere tutti i numeri reali, conteneva anche altri numeri che si comportavano in modo piuttosto strano. Alcuni di questi nuovi numeri risultavano essere maggiori di ogni numero reale, cioè erano da considerarsi numeri infiniti (sesto infinito!), ma dato che per ogni numero reale r esiste un inverso 1/r, e dato che i numeri iperreali hanno le stesse proprietà dei reali, per ogni numero iperreale infinito ω dovrà esistere un inverso 1/ω.
In realtà ci volle ancora qualche decennio, e almeno un altro matematico di genio, Abraham Robinson, ma alla fine diventò chiaro che questi numeri del tipo 1/ω erano proprio gli infinitesimi che aveva cercato invano di definire Leibniz. Hanno infatti la proprietà cruciale 0 < 1/ω < 1/n per ogni numero naturale n, oltre a ciò vale anche un’altra bellissima proprietà, cioè che ogni numero iperreale finito si può scomporre in modo univoco come somma di un numero reale r e di un infinitesimo 1/ω. Detto altrimenti ogni numero iperreale finito è infinitamente vicino (settimo infinito!) ad un solo numero reale.
Queste due proprietà danno immediatamente un fondamento logico inattaccabile al procedimento di Leibniz, basta usare un semplice accorgimento, ovverosia modificare la (1) come segue:
(*1) df(x)/dx=std( (f(x+dx)-f(x))/dx)
dove std(…) sta a indicare la funzione parte standard, cioè quella funzione che ad ogni numero iperreale finito associa la sua parte reale. Questa funzione è del tutto analoga alla funzione parte intera di un numero reale x (si indica [x]), che è quella funzione che per esempio a π associa il numero intero 3. Tornando al nostro famoso esempio le cose adesso vanno così:
d(x2)/dx=std(2x+dx)=2x
e non c’è più critica di Berkeley che tenga, poiché ora dx è un infinitesimo definito rigorosamente in termini di assiomi della logica formale, e anche la sua “scomparsa” dal risultato finale è perfettamente giustificata dall’utilizzo della funzione “parte standard”. Questo approccio al CI prende il nome di Analisi non Standard e a differenza dell'approccio classico, non lo troverete in nessun testo di Analisi matematica, nè in nessun corso universitario. Gli analisti (matematici s'intende) nutrono infatti un'ostinata avversione per questo modo di fondare la loro materia, quindi sebbene siano passati una cinquantina d'anni dalla sua prima formulazione l'Analisi non standard continua ad essere relegata a curiosità matematica, quando a mio avviso è di gran lunga superiore alla formalizzazione standard dell'Analisi.
A volte il parossismo nei confronti dell'Analisi non standard raggiunge vette notevoli, date un'occhiata a questo pdf , l'esempio in fondo a pag.14 mostra la risoluzione di un'equazione differenziale col metodo ribattezzato dall'autore urang-utang (si tratta in realtà del metodo non-standard dove viene omesso il passaggio finale alla funzione parte standard), poi confrontato con la soluzione ottenuta con il metodo standard, quello rrrigoroso...Se guardate bene, più avanti, in una noticina a pag.20, l'autore pare degnarsi di constatare che esiste un approoccio che dà senso a tutto ciò che ha deriso fino a quel punto, salvo poi metterlo subito da parte, visto che:
Cazzo, magari se iniziate a insegnarla nelle scuole, la gente saprà che esiste e potrà apprezzare il metodo nella sua semplicità antica, con l'aggiunta del rigore moderno. Ma finchè i soloni della materia continueranno a considerare l'Analisi non standard come una sofisticata giustificazione del perchè i metodi che ci dicono essere sbagliati funzionano, i poveri studenti dovranno continuare a mandare giù tonnellate di definizioni epsilon-delta e robe simili....sono convinto che la quasi totalità di chi pensa alla derivata
come rapporto tra infinitesimi non è in grado di utilizzare l’analisi non standard! Ammesso
che sappia che esista.
Per concludere, chi volesse approfondire può consultare un qualunque testo di Analisi matematica, seguono tutti lo stesso percorso di introduzione al CI. Oppure, se non dovete sostenere un esame universitario ma solo la vostra curiosità, potreste pensare di consultare questo splendido testo che è per giunta disponibile aggratis, anche se non esiste traduzione italiana, per quanto ne sappia. Direi che come prima (e forse unica) parte può bastare così.
FranZη
Si prega Accesso a partecipare alla conversazione.
grazie dello spazio concesso
e buon proseguimento !
milvalos
[mlv lu30ap18 00e29]
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
'e='e◦e'=e' !!!
Quello qui sopra non è un emoticon surrealista, bensì un teorema dell'algebra astratta, probabilmente fra i più generali che si possano enunciare. Volendo essere precisi sarebbe proprio la dimostrazione del teorema, ma una volta chiarito il significato dei simboli l'enunciato vi è contenuto. Purtroppo per chi legge questi chiarimenti non potranno essere concisi quanto la scrittura qui sopra, quindi chi vuole seguire il ragionamento deve avere un pochino di pazienza, ma farò del mio meglio per andare al sodo in fretta.
Come ogni edificio necessita un terreno preesistente su cui poggiare le proprie fondamenta, l'edificio matematico non fa eccezione. Già Euclide nei suoi Elementi segue questa strada, premettendo all'inizio dell'opera una lista di nozioni comuni e postulati, che sono un po' terreno e un po' fondamenta del suo edificio. Oggi le cose sono più complicate, ma schematizzando possiamo dire che le fondamenta della matematica moderna sono costituite dalla logica matematica, mentre le fondamenta di quest'ultima sono l'equivalente del terreno preesistente alla costruzione. Cosa sono dunque queste fondamenta ultime? Innanzitutto il linguaggio naturale, cioè l'italiano corrente nel nostro caso, o qualunque altra lingua che ci permetta di descrivere dall'esterno (dell'edificio) ciò che stiamo facendo, e che ci consenta di definire le nostre nozioni comuni, che non sono quelle di Euclide, ma sono ad esempio il concetto di insieme, di elemento, e la relazione di appartenenza.
L'algebra moderna, che nell'edificio matematico è solo un gradino sopra la logica nella scala della priorità epistemologica, si accontenta di partire da oggetti così generali e non definibili formalmente (in quanto enti primitivi) quali gli insiemi. Si parla di struttura algebrica quando abbiamo un insieme dotato di una legge di composizione interna, vale a dire un'operazione che presi due qualsiasi elementi dell'insieme ne associa loro un terzo. Le classiche operazioni di addizione e moltiplicazione su un insieme numerico sono l'archetipo di legge di composizione interna, ma le strutture algebriche possono essere di tipo infinitamente vario. Un esempio più esotico è dato dall'insieme delle stringhe di testo che si ottengono con i caratteri dell'alfabeto latino (chiamate "parole" anche in ambito matematico, con la differenza che qui anche "XHBUJHGD" va considerata una legittima parola), dove l'operazione consiste nella semplice giustapposizione, così che CASA+CHIESA=CASACHIESA.
Siccome a questo livello di generalità si preferisce non usare simboli che abbiano uno specifico significato, ecco che adotteremo un simbolo neutro per indicare l'operazione di una struttura algebrica, per esempio "◦" (e con ciò un primo simbolo nel teorema d'apertura assume significato...). Può accadere che una struttura algebrica possieda elementi con la particolare proprietà di non incidere sull'operazione, cioè elementi "e" tali che:
e◦a=a
per ogni altro elemento "a" della struttura. Questi elementi sono detti elementi neutri per ovvie ragioni. Nel caso delle operazioni + e x dell'aritmetica gli elementi neutri sono rispettivamente 0 e 1, mentre nella struttura data dalle stringhe di caratteri alfabetici l'elemento neutro è rappresentato dalla stringa vuota. Attenzione: non è la barra spaziatrice, la stringa vuota è proprio un carattere nullo, sarebbe un tasto che non ha effetto sullo schermo, o se preferiamo il cursore che lampeggia in attesa di un nuovo carattere.
Adesso serve una precisazione. La proprietà commutativa, ossia quella che ci garantisce che a◦b=b◦a per ogni coppia di elementi (a,b), è una proprietà molto specifica che al nostro livello di generalità non possiamo assumere, quindi occorrerà fare distinzione fra elementi neutri a sinistra ('e) ed elementi neutri a destra (e'), definiti dalle seguenti identità:
'e◦a=a
a◦e'=a
Questa distinzione è doverosa dato che, non valendo la proprietà commutativa, in generale 'e◦a non sarà uguale ad a◦'e, e lo stesso dicasi per e'. Un elemento che sia neutro sia a destra che a sinistra viene detto elemento neutro tout court. Ora abbiamo gli strumenti per enunciare il nostro teorema iniziale:
TEOREMA 1. Se in una struttura algebrica (A,◦) esiste sia un elemento neutro a sinistra 'e che un elemento neutro a destra e', allora questi coincidono.
La coppia (A,◦) identifica la struttura algebrica: A è l'insieme su cui è definita e ◦ l'operazione della struttura. La dimostrazione del teorema è quella data nell'incipit del post: consideriamo infatti la composizione dei due elementi neutri 'e◦e', questa è evidentemente uguale a 'e perchè e' è neutro a destra, ma anche ad e' dato che 'e è neutro a sinistra. Sembra una banalità, ma vi invito a riflettere sull'estrema generalità delle ipotesi e sull'affermazione molto circostanziata del teorema: è quasi un miracolo che in tale situazione si possa già dimostrare qualcosa! Dal Teorema 1 discende immediatamente un corollario, anch'esso piuttosto profondo:
COROLLARIO (TEOREMA 1). Una struttura algebrica ammette al più un elemento neutro.
La dimostrazione del corollario è immediata dato che un elemento neutro "e" è per definizione neutro sia a sinistra che a destra, quindi due elementi neutri e1, e2 devono per forza coincidere (basta anche qui considerarne la composizione e1◦e2). Bene, teorema e corollario appena dimostrati sono fra i più generali dell'algebra e dell'intera matematica. Ce ne sono altri simili, che richiedono solo qualche semplice ipotesi aggiuntiva. Consideriamo ad esempio la proprietà associativa, che finora non abbiamo incluso nelle ipotesi. Un'operazione si dice associativa se vale:
a◦(b◦c)=(a◦b)◦c
cioè se vale la semplificazione della parentesi, in tal caso è lecita la scrittura a◦b◦c in luogo delle due qui sopra con le parentesi. Può ora accadere che in una struttura algebrica associativa (esisterebbe tutta una terminologia tecnica per distinguere le strutture algebriche sulla base delle proprietà verificate, non mi sembra il caso di parlarne qui), dotata di elemento neutro "e", presi due elementi a,b risulti a◦b=e. In tal caso si dice che "a" è l'inverso sinistro di "b", e simmetricamente "b" l'inverso destro di "a". Preso un qualsiasi elemento "a" della struttura, usiamo le notazioni *a e a* per indicarne rispettivamente l'inverso sinistro e destro. Ecco allora il nostro secondo teorema-che-più-generale-non-si-può:
TEOREMA 2. Sia (A,◦) una struttura algebrica associativa dotata di elemento neutro e, se l'elemento a ammette sia un inverso sinistro *a che un inverso destro a*, allora questi coincidono.
dimostrazione:
Come noterete in questo caso la dimostrazione è un po' meno immediata, così ho numerato le righe per spiegare i passaggi. Innanzitutto abbiamo una catena di uguaglianze che ci porta dall'inverso sinistro *a a quello destro a*, stabilendone così l'identità, vediamo ora come. La riga 1 è semplicemente un'applicazione della definizione di elemento neutro, la riga 2 un'analoga applicazione della definizione di inverso destro, il passaggio 2--->3 è invece cruciale, ed è qui che abbiamo bisogno dell'ipotesi della proprietà associativa, senza quella non c'è la riga 3 e nemmeno il teorema. La riga 4 infine è perfettamente simmetrica alla 1, una banale applicazione di definizioni.
Consideriamo ora una struttura ancora un po' più complessa, o meglio uniamo due strutture algebriche costruite sullo stesso insieme A: abbiamo allora una cosa del tipo (A,♂,♀), dove ♂ e ♀ sono due distinte operazioni sullo stesso insieme. Strutture di questo tipo possono godere della fondamentale proprietà distributiva che lega le due leggi di composizione:
a ♀ (b ♂ c)=(a ♀ b) ♂ (a ♀ c)
Scritta così sembra incomprensibile, ma se usiamo le solite operazioni aritmetiche + e x è semplicemente:
a x (b+c)=(a x b)+(a x c)
Possiamo allora enunciare un ulteriore teorema generalissimo:
TEOREMA 3. Sia (A,♂,♀) una struttura algebrica con due operazioni associative legate dalla proprietà distributiva. Supponiamo che l'operazione ♂ sia dotata di elemento neutro e♂, e supponiamo inoltre che ogni elemento a dell'insieme A abbia un inverso rispetto all'operazione ♂. Allora per ogni a in A si ha:
a ♀ e♂ = e♂.
Anche qui, se al posto di ♂ e ♀ dicessimo + e x, il Teorema 3 afferma che a x 0 = 0 per ogni a. Cioè un numero moltiplicato per zero fa sempre zero. Beh, come vedete, e come dimostreremo subito, la cosa è assai più generale dell'ambito aritmetico.
dimostrazione:
(Siccome in fondo non vi voglio proprio male, uso i simboli + e x che tanto ci sono cari, a questo punto credo sia ormai chiaro che usando ♂ e ♀ funzionerebbe allo stesso modo, salvo il fatto che non si capirebbe un accidenti. Attenzione: l'inverso di "a" rispetto a "+" in quanto segue diventerà "-a", cioè quello che è comunemente l'inverso di "a" rispetto all'addizione. Analogamente userò "0" in luogo di e♂ per indicare l'elemento neutro della prima operazione.)
a x 0 = a x (a - a) = a x a - a x a = b - b = 0
Breve spiegazione. Anche in questo caso c'è una catena di uguaglianze che stabilisce l'identità del primo e dell'ultimo membro, che è l'enunciato del teorema. Il secondo e il terzo membro sono uguali per via della proprietà distributiva, mentre l'ultima uguaglianza b - b = 0 (che in realtà è a scopo chiarificatore, ma sarebbe facoltativa) si giustifica come segue. Non sappiamo quanto faccia a x a, dato che non abbiamo fatto nessuna ipotesi su cosa possa essere l'elemento "a" nè l'operazione "x" (che poi sarebbe ♀ se avessi voluto infierire), però sappiamo per ipotesi che deve per forza essere un elemento dell'insieme A, e noi allora lo chiamiamo "b". Quindi a x a - a x a = b - b. Ma b - b è la composizione di un elemento e del suo inverso (rispetto all'operazione +), quindi, sebbene non abbiamo idea di quale elemento sia e nemmeno di quale operazione stiamo facendo, sappiamo comunque che deve fare 0, per definizione di elemento inverso.
FranZη
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
(Qualche precisazione al topic "Terra Piatta: dibattito")
Dato che il thread Terra Piatta: dibattito è stato impostato come discussione a due, uso questo spazio per ripristinare un certo grado di verità fisica in alcune affermazioni del suddetto forum. Mi pare anche il caso di premettere che, così come in quella sede il dibattito è impostato in modo da escludere tutti gli altri utenti, in questa sede prego di non intervenire se non per chiarimenti o perchè si è veramente informati sul tema. Senza nessun intento polemico, gradirei solo che non ci fossero interventi ad mentula canis.
Veniamo ora al problema. La situazione è quella di un aereo che vola a una certa quota, in modo che la portanza generata dalle ali sia esattamente uguale e opposta alla forza di gravità, cito da un commento:
1- Una volta che l'aereo è in volo ovvero ha sviluppato abbastanza portanza da annullare la forza di gravità, quest'ultima non ha possibilità di interferire in nessun altra maniera con il “sistema aereo” perciò l'aereo sarà in grado di viaggiare perfettamente in linea retta.
Concentriamoci sulla figurina centrale, quella relativa alla posizione iniziale, poichè le altre due sono inferenze scorrette. In quest'altro commento si legge poi la seguente precisazione:
La forza risultante mentre un aereo vola è esclusivamente quella motrice che spinge l'aereo in avanti. La FdG è completamente azzerata/bilanciata dalla portanza, quindi secondo la relatività galileiana non è possibile avere una variazione della traiettoria.
Secondo Galileo, infatti, l'aereo semplicemente deve procedere in linea retta. Seguire la circonferenza della terra significherebbe seguire una linea curva.
Se vuoi che la gravità generi una accelerazione verso il basso, allora la portanza creata dall'aereo deve essere inferiore di quel tanto che basta, ovvero dovrebbe essere una scelta volontaria del pilota o del sistema di navigazione. Non mi risulta che si voli in questo modo anche perché la variazione di altitudine dovuta alla caduta dell'aereo, non incide sul beccheggio.
La seconda parte della citazione potrebbe generare confusione, perchè quello che conta nel discorso non è che a bilanciare la gravità sia la portanza, ma che ci sia una forza che istante per istante è uguale e contraria, qualunque sia la sua natura. Il discorso che andiamo a fare in effetti vale anche per i satelliti, che come è noto non stanno in quota grazie alla portanza. Allora, partiamo da Galileo e dal suo principio di inerzia: un corpo non soggetto a forze si muove di moto rettilineo uniforme. Bene, dato che nel post Calcolo Infinitesimale qui sopra ho introdotto il rapporto esistente fra Analisi e Fisica, possiamo usare i concetti già esposti e quindi partiamo dal fatto che l'accelerazione è la derivata seconda dello spazio rispetto al tempo.
In assenza di forze siamo nella situazione F=ma=0, quindi l'accelerazione a è zero (altrimenti dovrebbe essere zero la massa m, cioè non ci sarebbe alcun corpo di cui discutere). Ricordo che la posizione di un corpo istante per istante è data dalla sua legge oraria , se per semplicità ipotizziamo che il moto si svolga in un piano questa avrà la forma:
s(t)=( x(t),y(t))
dove la variabile t indica il tempo e x(t), y(t) sono due funzioni che forniscono le due coordinate cartesiane che il corpo occupa all'istante t. Con ciò ovviamente il corpo si suppone puntiforme, altra semplificazione molto vantaggiosa nel nostro caso. Dunque dicevamo che l'accelerazione è nulla, questo si traduce nelle due equazioni (differenziali, ma non spaventatevi...):
d2x/dt2=0
d2y/dt2=0
...cioè le derivate seconde rispetto al tempo sono identicamente nulle. La soluzione generale del sistema di equazioni è:
x(t)=v0xt+s0x
y(t)=v0yt+s0y
dove v0x, v0y sono due costanti che hanno il significato fisico di velocità iniziale lungo l'asse x e y rispettivamente, mentre s0x e s0y rappresentano la posizione iniziale del punto, in coordinate cartesiane ovviamente. Quella descritta dalle equazioni qui sopra è una retta che il punto percorre con velocità costante v=sqrt(v0x2+v0y2) al variare del tempo t, e nell'istante iniziale t=0 il punto si trova in (s0x,s0y). Ecco allora che abbiamo dedotto il principio d'inerzia, già enunciato sopra, via passaggi puramente matematici direttamente dall'ipotesi che non ci siano forze agenti sul corpo .
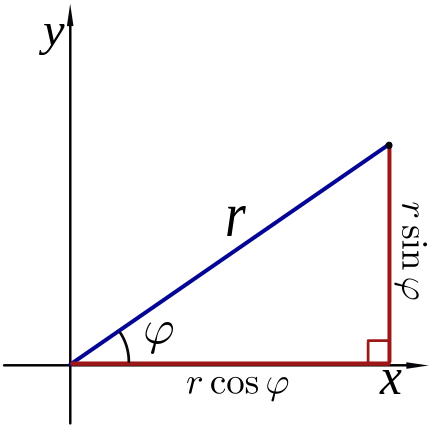
Questa però non è la situazione dell'aereo descritta all'inizio. Per rendersene conto è conveniente passare alle coordinate polari r(t),φ(t) legate alle x(t),y(t) dalle relazioni riportate in figura:
A questo punto il fatto che la forza di gravità sia esattamente compensata dalla portanza si traduce nella seguente equazione differenziale:
d2r/dt2=0
che ci dice che l'accelerazione lungo la componente radiale r(t) è sempre nulla. La soluzione generale in questo caso è:
r(t)=v0rt+r0
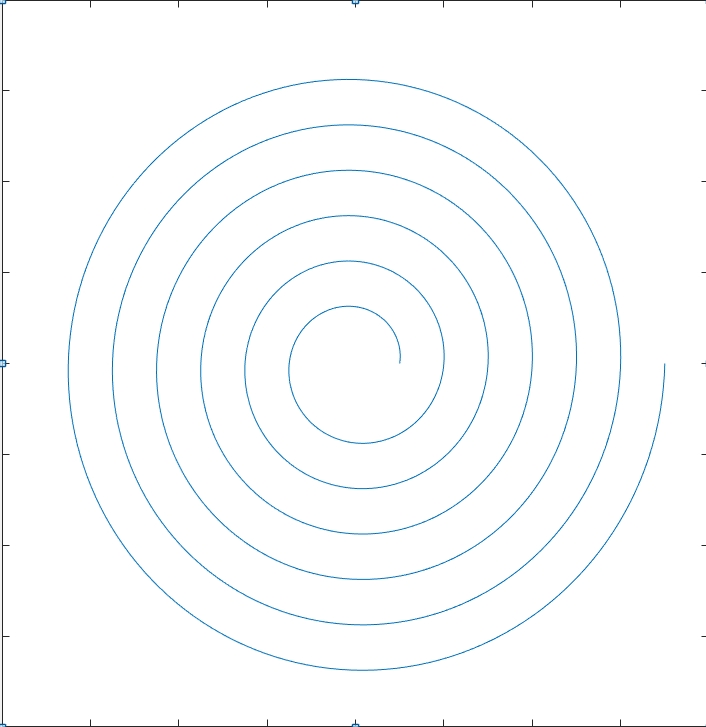
con v0r e r0 rispettivamente velocità e posizione radiale iniziale, soluzione che non corrisponde a una linea retta, bensì a una spirale:
Per tracciare il grafico sopra ho posto v0r e r0 uguali a 1. Questa come dicevo è la soluzione generale, ma nel nostro caso sappiamo che v0r=0, perchè all'istante iniziale l'aereo vola perfettamente livellato, ecco allora che la nostra spirale diventa una circonferenza di raggio r0, che sarebbe poi la somma della quota dell'aereo e del raggio terrestre. Non solo: il fatto che la forza di gravità sia costante in modulo (a una data quota di altezza) ci porta a concludere che anche il moto angolare deve essere costante:
φ(t)=ω0t+φ0
dove ω0 è la velocità angolare e φ0 la posizione (angolare), entrambe all'istante iniziale t=0. Il nostro aereo si muove dunque di moto circolare uniforme, in accordo con la relatività galileiana. Va precisato che in effetti se l'accelerazione radiale è uguale a zero significa che la forza di gravità è uguagliata dalla somma della portanza e della forza centrifuga dovuta al moto circolare. In quanto precede ho tralasciato quest'ultima forza poichè:
- nel caso dell'aereo è del tutto trascurabile;
- avrei rovinato la "sorpresona" finale nello scoprire un moto circolare;
- sarebbe stata una complicazione inessenziale.
Tuttavia nel caso del moto di un satellite, essendo pari a zero la portanza, sarebbe solo la forza centrifuga a intervenire per controbilanciare la gravità.
***********************
Chiarito come si imposta il problema fisico dell'aereo, mi sembra il caso di fare una precisazione anche sul discorso del pendolo di Foucault, che è stato liquidato in modo sbrigativo. Il pendolo di Foucault infatti non si limita a ruotare, ma ruota con una velocità angolare proporzionale alla latitudine. Per la precisione la rotazione oraria del pendolo è data da:
α=360°/24*sin(λ)
dove λ è la latitudine alla quale il pendolo è posizionato. Alle nostre latitudini (45°) la rotazione α è di 10.6° ogni ora. Si noti che nell'emisfero australe la formula comporta una rotazione invertita, cosa che si verifica sperimentalmente. Quindi la sfericità della terra è una conseguenza indiretta dell'esperimento di Foucault: deriva dal fatto che sperimentalmente si ottengono velocità di rotazione proporzionali a sin(λ), se gli esperimenti avessero evidenziato che la rotazione è indipendente dalla latitudine, beh, quella sarebbe stata una prova che la terra gira, ma è piatta.
FranZη
Si prega Accesso a partecipare alla conversazione.
- Michele Pirola
-

- Offline
- Utente
-

- Messaggi: 668
- Ringraziamenti ricevuti 27
- Messaggi: 850
- Ringraziamenti ricevuti 118
Cos'è il Genio?Michele Pirola ha scritto:
È fantasia, intuizione, colpo d'occhio e velocità d'esecuzione.
FranZη
Si prega Accesso a partecipare alla conversazione.
- Michele Pirola
-

- Offline
- Utente
-

- Messaggi: 668
- Ringraziamenti ricevuti 27
FranZeta ha scritto:
Cos'è il Genio?Michele Pirola ha scritto:
È fantasia, intuizione, colpo d'occhio e velocità d'esecuzione.
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Riprendiamo dalle origini, con un argomento tratto dal libro Contattismi di massa di Stefano Breccia, già citato nel primo post di questo forum. Questa volta si va direttamente a prendere in considerazione materiale alieno, anche se la matematica sottostante è tutta terrestre. O meglio: è anche terrestre, d'altronde non è certo un'idea mia che se mai può esistere un linguaggio universale questo avrà a che fare con la matematica.
Gli ummiti sono questo simpatico gruppo di extraterrestri provenienti, per l'appunto, dal pianeta Ummo, distante una decina di anni luce dalla Terra. A partire dagli anni sessanta hanno intrattenuto un lungo rapporto epistolare con un gruppo di terrestri, per lo più spagnoli, nel quale parlano un po' di tutto comprese alcune informazioni relative alla loro matematica. Qui trovate la raccolta della corrispondenza, in spagnolo e francese più alcune traduzioni in italiano. In tempi recenti hanno iniziato pure a twittare!
Non mi pare il caso di intavolare qui una discussione sull'attendibilità o meno del contattismo ummita (o del contattismo in generale), si tratta comunque di un fenomeno interessante e per quanto riguarda i contenuti matematici, ma anche fisici, degno di considerazione. Come già avevo accennato nel thread Amicizia , in una di queste lettere anticipano l'esistenza di una dimostrazione dell'Ultimo teorema di Fermat, cosa di per sè non sconvolgente, va però sottolineato che all'epoca nella comunità matematica non erano pochi quelli che dubitavano dell'esistenza di tale dimostrazione, non fosse altro per il fatto che dopo tre secoli e mezzo di ricerca da parte delle migliori menti matematiche non se ne era ancora venuti a capo. E infatti quando un paio di anni più tardi Andrew Wiles annunciò al mondo di aver risolto il problema lo stupore fu grande.
Per quanto riguarda la fisica, oltre a una panoramica generale sugli enti fondamentali che regolano il nostro universo, e a questo proposito vi rimando al mio post successivo sempre nel thread Amicizia, fanno una previsione a mio avviso tanto avventata quanto poi rivelatasi azzeccata. Scusate ma al momento non ho tempo di cercare la lettera in cui affermano quanto segue, per cui fidatevi della mia memoria. Siamo alla fine degli anni '60, da poco nella fisica delle particelle è stata teorizzata la particella nota come quark, e i nostri ummiti in una delle loro missive spiegano che questi quark non esistono affatto e se dovessimo proseguire su tale linea di pensiero la nostra fisica resterebbe al palo per un lungo periodo. Beh, potete vederla come volete ma è un fatto che la fisica degli ultimi cinquant'anni ha prodotto ben poco di utile a livello di teorie fondamentali. E stiamo ancora a giocare coi quark...
Detto ciò veniamo al nostro argomento. Gli ummiti spiegano che anche loro utilizzano l'equivalente del nostro piano cartesiano (R2 - si legge erre-due e non erre-quadro! - come lo chiamano i matematici) solo che hanno un diverso sistema di coordinate, che ora andiamo ad illustrare. Anzi, prima di tutto ricordiamo qual è il nostro sistema di coordinate: è quello in cui ogni punto è identificato dalla coppia di coordinate x e y, anche dette rispettivamente ascissa e ordinata, ossia i punti sono individuati così:
P=(xP,yP)
Il sistema di riferimento è individuato da due rette perpendicolari, gli assi x e y, e la loro intersezione è l'origine del piano, vale a dire il punto di coordinate (0,0). In questo sistema di coordinate un'equazione che coinvolga le incognite x e y corrisponde a un certo insieme di punti del piano, in particolare le equazioni polinomiali, cioè quelle del tipo f(x,y)=0 dove f è un polinomio che contiene (solo) le incognite x,y, definiscono delle curve algebriche nel piano. Queste curve si classificano in base al grado del polinomio f: quelle di grado 1 sono le rette, di grado 2 le coniche, di grado 3 le cubiche e via così.
Il nostro piano cartesiano col suo sistema di coordinate ortogonali è in definitiva una sorta di scacchiera ampliabile a piacere e con caselle piccole a piacere. Il piano con coordinate ummite invece assomiglia di più a una rappresentazione 3D - con visione binoculare dunque - di questa scacchiera. Innanzitutto per stabilire il riferimento ummita si scelgono due punti distinti del piano, A e B. Come facciamo a sapere quali sono, se non abbiamo ancora un sistema di coordinate, direte voi. Esattamente come facciamo col nostro piano cartesiano: non lo sappiamo! Cerco di spiegarmi meglio: il piano R2 va considerato come preesistente e indipendente dal nostro sistema di coordinate. E' un ente matematico con le sue proprietà che non dipendono da come decidiamo di individuare i suoi punti, così come le proprietà (e LA proprietà...) della vostra casa non dipendono dal numero civico o dal nome della via: se domani cambiano nome alla via cambia il vostro indirizzo, non il vostro salotto! Allo stesso modo quando noi diciamo "questo punto è l'origne del piano" ne stiamo prendendo uno a caso, anche perchè il piano cartesiano non ha punti privilegiati rispetto ad altri.
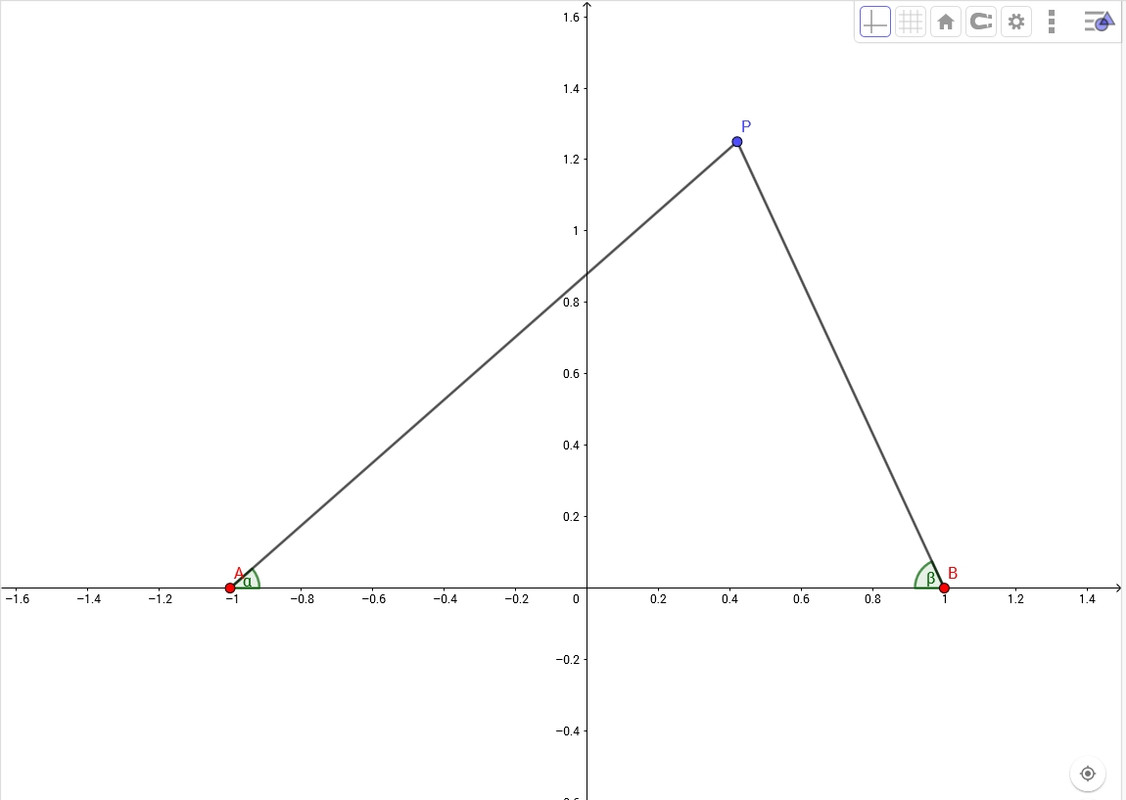
Dunque anche gli ummiti scelgono due punti arbitrari A e B e poi, per individuare un generico punto P, usano semplicemente i due angoli α=BAP e β=ABP:
Nell'immagine ho mantenuto i nostri cari assi cartesiani per comodità e confronto, ma usando il sistema di coordinate ummita sono del tutto inutili. Sempre per comodità ho posizionato A e B rispettivamente in (-1,0) e (1,0), questo ci permetterà di trovare una particolare conversione fra i due sistemi di coordinate, ma ancora ripeto: A e B possono essere in qualunque posizione, così come il nostro O con i suoi assi x e y d'altronde. Si noti che α si misura in senso antiorario e β in senso orario. Queste sono le espressioni delle coordinate ummite rispetto alle nostre:
dove con "l" ho indicato la distanza dall'origine dei due punti A e B (ho quindi generalizzato un pochino lo schema sopra: i due punti hanno cioè coordinate (-l,0) e (l,0), nel caso particolare di prima era l=1). Queste invece sono le espressioni inverse, quelle delle coordinate cartesiane in funzione delle ummite:
Immaginate che i punti A e B corrispondano al centro dei vostri occhi, immaginate anche un qualsiasi piano passante per detti centri oculari, le coordinate ummite vi consentirebbero di individuare un punto qualsiasi di questo piano semplicemente misurando l'angolo individuato dalle vostre pupille rispetto all'asse passante per i centri oculari. Ipotizzando di non muovere il collo, ovviamente. Dunque in tale riferimento un punto generico è individuato da:
P=(α,β)
Non tutti i punti del piano cartesiano possono però essere individuati con queste coordinate: restano esclusi i punti della retta passante per A e B. Ciò non deve sorprendere dato che anche nella visione umana c'è un limite naturale invalicabile prima dei 180° di ampiezza. Lo stesso vale per gli obiettivi fotografici. Quindi in quanto angoli e per le limitazioni appena esposte le due coordinate α e β sono definite nell'intervallo aperto (-π,π) escluso il valore 0. A differenza delle coordinate cartesiane, dove ogni coppia di valori (x,y) è ammissibile e definisce un unico punto, le coordinate ummite devono sottostare all'ulteriore condizione che la loro somma sia, in modulo, minore di π, altrimenti le due semirette non si incontrerebbero ma sarebbero parallele o divergenti. Si deve avere cioè
|α+β| < π
dove il modulo è necessario perchè ad angoli negativi corrispondono punti al di sotto dell'asse x. Infine α e β devono avere lo stesso segno. Tutto ciò le rende piuttosto scomode da usare nei corsi di geometria, però questo non toglie la naturalezza del sistema di coordinate in riferimento alla fisiologia della visione binoculare.
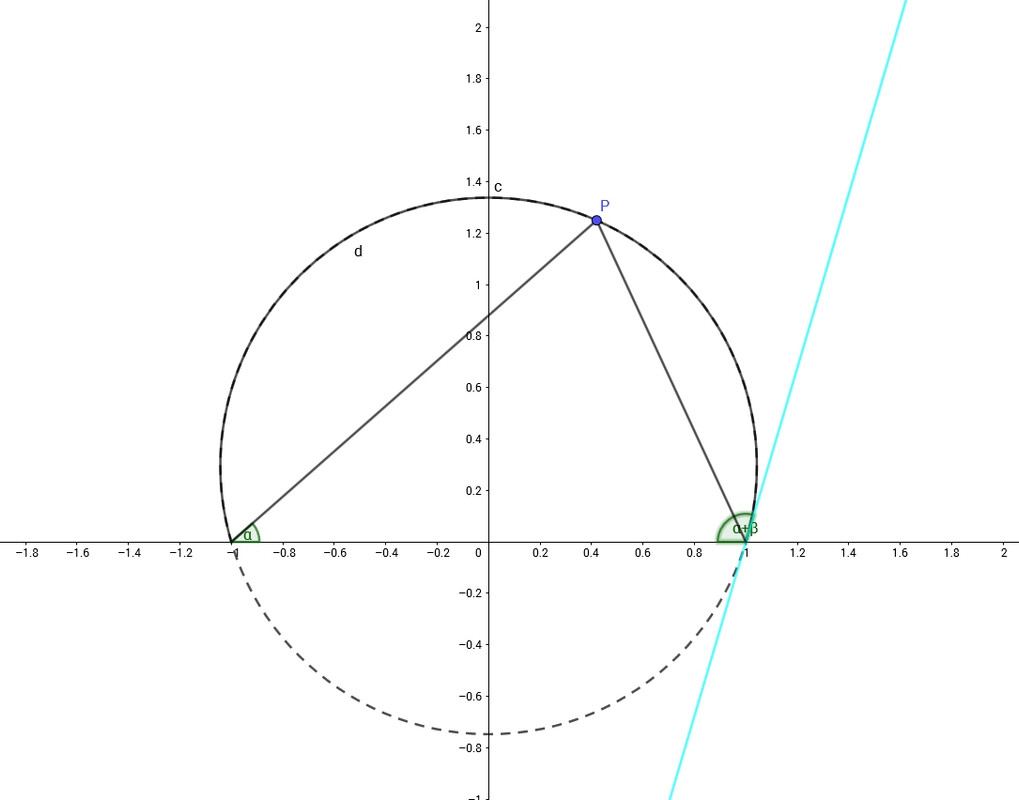
Stefano Breccia nel suo libro fa notare che all'equazione α+β=c, con c costante arbitraria, corrisponde una circonferenza del piano. Questa affermazione però è piuttosto imprecisa, infatti, anche sorvolando sul fatto che la costante c deve essere minore di π, in realtà l'equazione sopra definisce solo un arco di circonferenza compreso fra A e B. Vediamo la cosa più in dettaglio:
Consideriamo dunque la circonferenza passante per A,B e P. Come ricorderemo dalla geometria elementare un angolo alla circonferenza è esattamente la metà dell'angolo al centro che insiste sulla stessa corda, corollario del teorema è che tutti gli angoli alla circonferenza che insistono sulla stessa corda sono uguali. Nel nostro caso il segmento AB è una corda e l'angolo APB è un angolo alla circonferenza che insiste sulla corda. Inoltre, sempre dalla geometria elementare, sappiamo che la somma degli angoli di un triangolo è π (cioè 180°, esprimo sempre gli angoli in radianti come d'altronde dichiarano di fare gli stessi ummiti), da ciò segue che:
APB=π-α-β=π-(α+β)
Ecco allora che se l'angolo APB è costante, e dunque P sta su un arco di circonferenza compreso tra A e B, anche α+β risulta essere costante, ossia vale l'equazione α+β=c. Questa c si ricava facilmente considerando il caso limite in cui P coincide con B, in tal caso α=0, β=c e l'angolo cercato è quello formato dalla retta AB e dalla tangente alla circonferenza in B (retta azzurra). Questo ci fornisce una procedura pratica per trovare l'arco di circonferenza corrispondente all'equazione α+β=c: si traccia in B la retta azzurra con inclinazione c rispetto alla retta AB (l'angolo si misura in senso orario, come per β) e poi si traccia la circonferenza tangente a questa retta e passante per A e B.
A questo punto è chiaro che non tutta la circonferenza è definita da questa equazione, la parte della curva tratteggiata non può soddisfare l'equazione per la stessa costante c, infatti dalla figura si vede facilmente, ragionando sempre sulla tangente in B, che l'arco tratteggiato della circonferenza soddisfa l'analoga equazione α+β=c-π. Non essersi accorto di questo semplice fatto porta poi Breccia a scrivere altre cose sbagliate. Infatti prosegue così:
Non è difficile dimostrare che le equazioni del tipo:
α-β=c
con c costante, rappresentano delle iperboli, con asintoti variamente orientati.
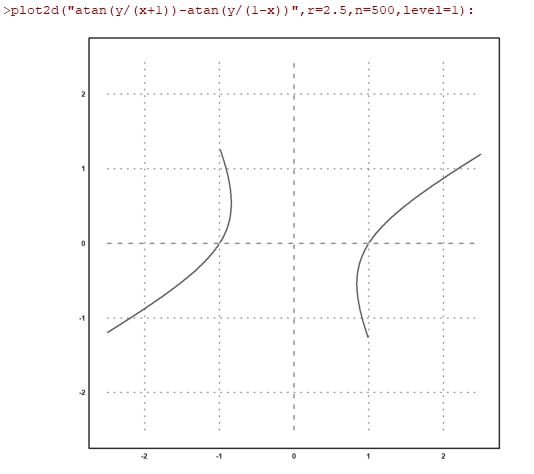
Ecco, siamo ancora in un caso analogo alle circonferenze, infatti l'equazione sopra rappresenta solo degli archi di iperbole, come ad esempio questa:
...e la cosa non dovrebbe stupire chi fosse incorso in questo precedente post dove si spiegava che un'iperbole altro non è che una circonferenza che interseca la retta all'infinito...Ma vediamo cos'altro dice Breccia:
Divertente il caso particolare allorchè α=0 [qui c'è un refuso, da quanto segue è evidente che intendeva α=β]. Il luogo risultante è costituito dalla coppia dei convenzionali assi cartesiani ortogonali! Difatti, per α ǂ 0, la funzione risultante è l'asse delle ordinate, in quanto i punti P si trovano ad essere il vertice superiore di triangoli isosceli, quindi descrivono la retta x=0.
Fin qui tutto bene, salvo ricordare che il punto (0,0) è escluso da questa rappresentazione. Ma poi:
Per α=0, si ha di conseguenza β=0 [No!!!] ed il triangolo ABP degenera nella retta y=0. Realmente divertente, anche se facilmente immaginabile: difatti anche in metrica cartesiano gli assi di riferimento sono il caso limite di una famiglia di iperboli.
L'ultima affermazione è corretta, senonchè non avendo ancora realizzato che i luoghi geometrici di cui parla non sono circonferenze o iperboli ma solo archi di questi, Breccia non realizza nemmeno che sarebbe difficile trovare rette come caso limite di archi, ma sarebbe più logico trovare segmenti. E infatti, se poniamo α=β=0, dalla prima figura del post è facile vedere che a queste equazioni corrispondono tutti i punti del segmento AB, senza che se ne possa scegliere uno in particolare. Quindi volendo dare un senso anche ai casi degeneri, l'equazione α=β corrisponde all'asse y più il segmento AB. Possiamo discutere se gli estremi del segmento siano inclusi o meno, in effetti il punto B potrebbe essere identificato da (α=0,β qualsiasi) e analogamente A da (α qualsiasi,β=0), quindi potremmo includere gli estremi. In ogni caso le due semirette (-∞,A) e (B,+∞) non possono essere descritte dall'equazione proposta da Breccia. Anche qui, se vogliamo proprio proseguire in questa piuttosto inutile analisi dei casi degeneri (inutile perchè il sistema di coordinate in questi casi non è valido, caratteristica fondamentale di un sistema di coordinate è che identifichi univocamente i punti!), la prima semiretta corrisponderebbe alle equazioni (α=π,β=0) e la seconda a (α=0,β=π). Insomma, proprio i valori che noi all'inizio avevamo escluso esplicitamente, onde non incorrere in degenerazioni e denominatori che si annullano...
A costo di infierire sul povero Breccia (che però, in quanto ingegnere, certe cose sarebbe anche stato tenuto a saperle...) faccio notare un'ulteriore confusione in quanto afferma nel paragrafo seguente:
Non parrebbe agevole l'estensione alle tre dimensioni, se non fosse per un concetto apparentemente strampalato citato dagli Ummiti nella loro descrizione dello spazio. Secondo loro, lo spazio è, sì, composto da una triplice infinità di punti (pensando a tre dimensioni), ma ad ogni punto è associata una triplice infinità di angoli fra direzioni...
...
...imporre una funzione di variazione di tali angoli (da loro chiamati IBOZOO UU) genera qualunque struttura.
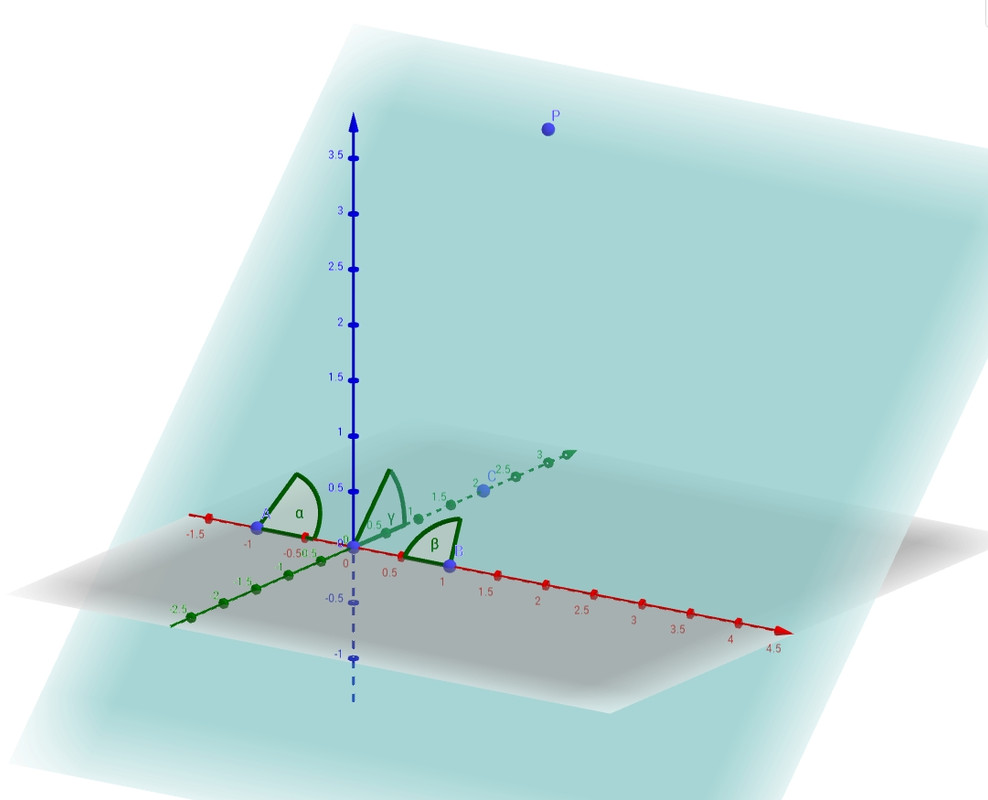
Stop. Estendere il loro sistema di coordinate a tre dimensioni è estremamente semplice e naturale: ricordate il parallelo fatto all'inizio con la visione binoculare? Ho dovuto premettere che bisognava prima scegliere un particolare piano passante per i centri degli occhi, perchè ovviamente la visione è relativa al mondo 3D. Quindi per estendere il sistema allo spazio tridimensionale basta prendere un piano di riferimento fra gli infiniti che passano per i due punti A e B, per farlo basta scegliere un ulteriore punto C (per tre punti passa un unico piano). Adesso per individuare un generico punto punto P nello spazio tridimensionale R3 (si legge erre-tre e non erre-cubo!) basta procedere come segue: innanzitutto si ruota il piano di riferimento passante per ABC lungo l'asse AB fino a farlo coincidere con il piano ABP, l'angolo corrispondente a questa rotazione, chiamiamolo γ, è la terza coordinata che ci serve per determinare P, infatti una volta che siamo nel piano ABP possiamo usare le coordinate ummite bidimensionali. In definitiva il punto risulta determinato dalla terna:
P=(α,β,γ)
Anche nel caso tridimensionale resta esclusa dal sistema di coordinate la retta passante per AB. Per quanto riguarda gli IBOZOO UU rimando di nuovo ai post del thread Amicizia, sottolineando che gli Ummiti avvertono esplicitamente e reiteratamente che queste entità fondamentali, pur avendo una natura angolare (e dimensione dieci, per la cronaca), non vanno confuse con gli angoli della nostra geometria, pena il non capirne il significato. Non scomodiamo quindi i "bosi", come li chiamo io, i cari vecchi angoli di greca eredità sono più che sufficienti qui.
FranZη
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
P=(x,y,z,w)
è un generico punto dello spazio quadridimensionale indicato col sistema di coordinate cartesiane. La nuova coordinata w ha lo stesso significato delle altre: è un qualsiasi numero reale. L'origine di tale sistema di coordinate è semplicemente il punto O=(0,0,0,0). Con la stessa naturalezza possiamo estendere il sistema di coordinate ummite a qualsiasi dimensione, ragionando per induzione. Nel caso bidimensionale il generico punto P è individuato come vertice di un triangolo di base AB mediante i due angoli α,β. Passando in dimensione 3 il punto P è il vertice di un tetraedro di base ABC individuato dai tre angoli α,β,γ. Diventa allora chiaro come generalizzare il tutto: in dimensione 4, P diventa il vertice di un ipertetraedro* di base ABCD, dove D è un nuovo punto di riferimento aggiunto al sistema ummita (allo stesso modo per cui l'asse w è un nuovo asse di riferimento aggiunto al sistema cartesiano). P risulta allora individuato dai quattro angoli α,β,γ,δ, dove δ è l'angolo che misura l'inclinazione del tetraedro ABCP rispetto a ABCD.
*Un ipertetraedro è un tetraedro di dimensione maggiore di 3. In dimensione 4 si può visualizzare così:
Si tratta della proiezione nello spazio tridimensionale del tetraedro quadridimensionale (in realtà è un'ulteriore proiezione 2D di questa, dato che sta nello schermo del computer, immaginatevelo in 3D...), è composto da cinque facce ognuna delle quali è un tetraedro tridimensionale, i tetraedri in questione sono ABCP, ABDP, ACDP, BCDP e...ABCD! Si noti che l'ultima faccia "contiene" le altre, ma questo è un effetto della proiezione, in realtà ogni faccia ha lo stesso ruolo delle altre, così come nella proiezione del cubo in basso a destra:
...una faccia sembra contenere le altre. Per la cronaca la stessa proiezione di un ipercubo è questa:
Si noti come si segua questa progressione: un triangolo (dimensione 2) ha 3 facce costituite da segmenti (= "triangoli" di dimensione 1), un tetraedro 4 facce costituite da triangoli, un ipertetraedro di dimensione 4 ha 5 facce costituite da tetraedri ("triangoli" di dimensione 3), e così via... quindi un tetraedro di dimensione n avrà n+1 facce costituite da "triangoli" di dimensione n-1!
FranZη
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Ufficialmente pi greco e sezione aurea (3.141592... e 1.618033... rispettivamente) sono numeri ignoti agli egizi del 2500 a.C.: solo a partire da circa 2000 anni più tardi si affacciano nel mondo greco, e in forma assai diversa da quella che conosciamo noi, ad esempio il simbolo π è stato usato per primo da Eulero per indicare il rapporto fra circonferenza e diametro del cerchio, e solo un secolo più tardi sarà riconosciuto come numero trascendente. Per qualche dettaglio in più sulla sezione aurea Φ rimando al primo post di questo thread. Insomma, accostare gli egizi della IV Dinastia a questi due numeri è considerata un eresia. Cito da Storia della matematica di Carl B. Boyer:
L'ipotesi che il rapporto tra il perimetro della base e l'altezza della Grande Piramide fosse stato consapevolmente stabilito in 2π è chiaramente in contraddizione con le nostre conoscenze sulla geometria degli egiziani.
Ora, a parte il fatto che in generale Boyer è un eccellente storico della matematica e il suo libro è vivamente consigliato a prescindere dalla citazione qui sopra, che tra l'altro Boyer riprende da un certo N.F.Wheeler e dal suo Pyramids and Their Purpose (suppongo che ci sarebbe parecchio da ridere a leggere quel testo...), a parte questo dicevo, il rapporto in questione è 6.2908, con uno scarto dal valore di 2π dello 0.12%...ma come cazzo si fa a sostenere che è casuale?
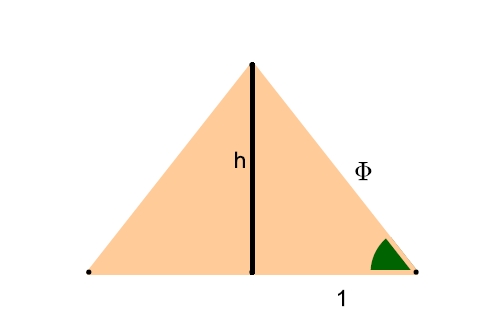
Ma c'è di più. Anni fa, dopo aver sentito Angela padre o figlio ripetere questa manfrina del rapporto casuale, ho dedicato un piccolo studio alla questione, ed è saltato fuori che la cosa è ancora più strabiliante...altro che π approssimato allo 0.12%! L'angolo alla base della Grande Piramide misura 51°49′13′′, quest'angolo differisce di soli 25 secondi d'arco (ossia meno di 0.007°, un margine d'errore non solo trascurabile ma anche attribuibile alle misurazioni moderne) da quest'altro angolo: α=51°49'38''. Cos'ha di speciale α? Ecco:
Quella del disegno è la sezione centrale di una piramide con angolo alla base α, in tale piramide è codificata la sezione aurea Φ, come rapporto fra ipotenusa e cateto minore dei due triangoli rettangoli che compongono la sezione. Sezione aurea che ricordo era ufficialmente sconosciuta agli egizi del 2500 a.C. e ad ogni altro popolo dei 2000 anni successivi. Non solo. L'altezza h risulta essere uguale alla radice quadrata di Φ, ecco allora che il rapporto fra altezza e perimetro della piramide è 8/Φ1/2=6.2892, che oltre ad essere un'ottima approssimazione di 2π, è praticamente il rapporto effettivo della Grande Piramide (errore 0.025%) già riportato sopra. Ricapitolando: le dimensioni relative della Grande Piramide, che come per ogni piramide sono fissate dall'angolo di inclinazione delle facce, conducono senza ambiguità alla seguente "quasi" identità matematica:
4/Φ1/2 ≈ π
dove il simbolo "≈" sta per "circa uguale" e il margine di errore del "circa" è quantificabile nello 0,025%. Per dire, avete presente le ruote della vostra auto? Ecco, l'eccentricità dello pneumatico può essere anche 10 volte maggiore rispetto a questo margine d'errore, senza che ciò comprometta le funzionalità della ruota o generi vibrazioni avvertibili. Se egittologi/archeologi vari facessero i gommisti, dovrebbero inevitabilmente concludere che gli pneumatici sono di forma circolare per pura coincidenza! Beh, almeno questo è il loro atteggiamento verso le misure delle piramidi.
Ci sarebbe ancora qualcosa da dire su queste misure. Abbiamo visto che il triangolo rettangolo sezione della piramide ha le seguenti proporzioni dei lati: 1, Φ1/2, Φ. Questo suggerisce una progressione geometrica di ragione Φ1/2, ossia la successione:
(Φn/2)nϵN = 1, Φ1/2, Φ, Φ3/2, Φ2,...
...successione che ha una singolare proprietà: sebbene la base della successione sia un numero irrazionale, Φ1/2, da un certo punto in poi iniziano a comparire numeri quasi interi. Ecco i primi 100 termini della successione, troncati al quarto decimale:
Come potete verificare, alla nona riga compare il primo numero "intero", 24476. Si tratta in realtà di un numero irrazionale le cui prime quattro cifre decimali sono zero. Da lì in poi questi numeri quasi interi compaiono in sequenza alternata, i numeri che li inframezzano sono corrispondenti agli esponenti semi-interi, dunque la successione (Φn)nϵN costituita dai soli esponenti interi da un certo punto in avanti contiene solo numeri quasi interi. Coincidenze.
FranZη
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
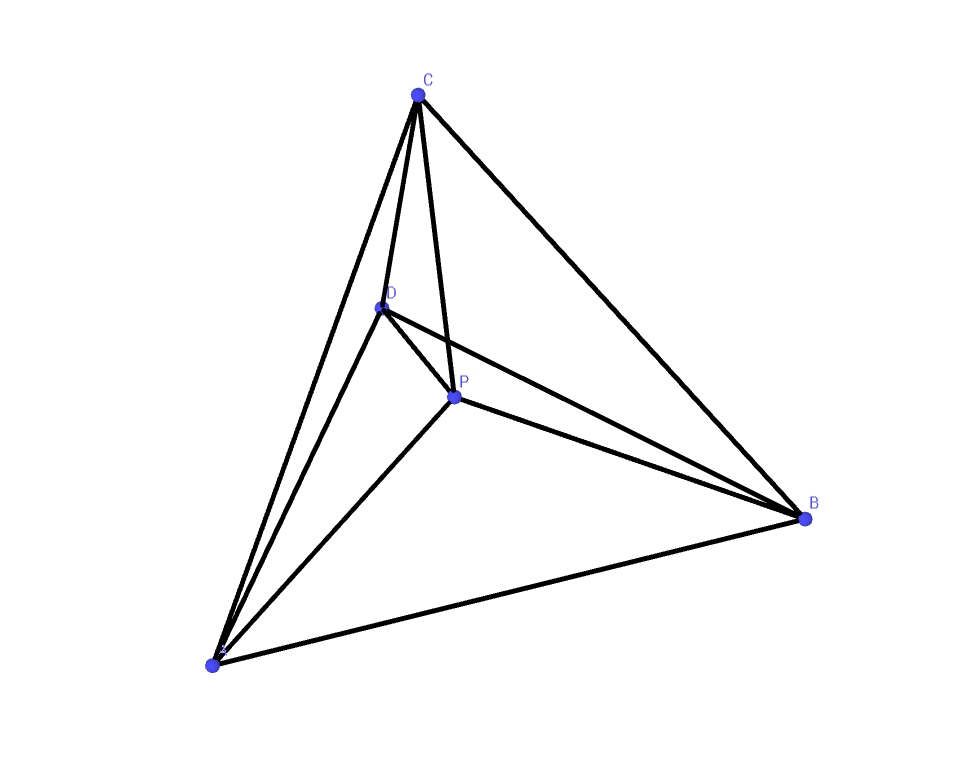
Ora, siccome l'utente Bandini si è convinto per autosuggestione che esistano dei tiranti permanenti all'interno dell'impalcato fra i punti C e F, cioè dei cavi tesi passanti per C-D-E-F, ha voluto apostrofare il mio intervento sopra linkato con frasi del tipo:
Confondi stralli con cavi provvisionali, non capendo la funzione che hanno.
Il vero problema è che inquini la discussione argomenti tecnici che evidentemente non padroneggi e così facendo induci altri a fare valutazioni errate.
Al che ho replicato con il seguente:
Allora siccome mi hai dato due volte di quello che non capisce niente e adesso dici pure che inquino la discussione, ora o mi dici esattamente dove si parla di tiranti diversi dagli stralli, oppure quello che non ha capito un cazzo sei tu e dovresti ritirarti un buon ordine.
La risposta di Bandini è quella che vado ora a discutere in dettaglio.
No caro Bandini, non ho chiesto nessuna spiegazione, ho chiesto un riferimento bibliografico alla parte del documento in cui si parla di tiranti definitivi diversi dagli stralli. Era peraltro una domanda retorica, dato che questi tiranti te li sei inventati tu. Proseguiamo:Non è mia intenzione offendere, visto che lo chiedi lo rispiego.
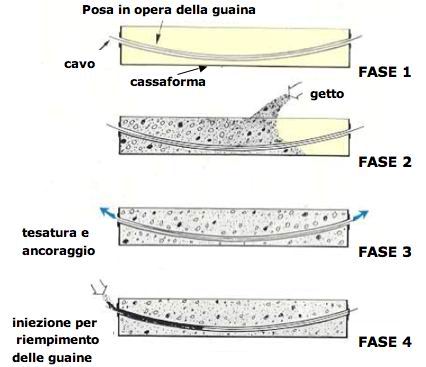
Il paragrafo che segue è riferito alla travata in cemento armato precompresso. E' stata prima gettata e poi precompressa (la travata) con i tiranti definitivi. Ma fino al momento della precompressione finale il getto non poteva reggersi con tutto quello sbalzo senza la posa dei tiranti provvisionali. Qui non si parla dei tiranti all'interno degli stralli ma dei tiranti all'interno della travata.
Ecco, appunto: invenzione di Bandini, dato che la successiva citazione dal pdf spiega tutt'altro:
"il getto dei tratti C-D ed E-F della travata è avvenuto utilizzando il noto metodo "peu a peu". Si è trattato cioè di eseguire ogni tratto in 13 conci successivi della lunghezza di 5,13 m, ciascuno affidato al resto della struttura a mezzo di un sistema di cavi pretesi superiori, esterni e provvisionali, che si sono tolti dopo aver ultimato la loro funzione, sostituita, come è noto, da un certo momento in poi, dall'azione longitudinale orizzontale dei tiranti definitivi. Questi cavi, di andamento sub-orizzontale, hanno assunto la loro configurazione prestabilita a mezzo di due piccoli cavalletti provvisori costruiti in corrispondenza dei punti D ed E".
Ora, è evidente che questi tiranti definitivi di cui si parla qui non sono meglio specificati, ma per un buon motivo: erano gli stralli, cioè l'elemento più evidente dell'intera costruzione. Tanto è vero che si premurano di specificare che l'azione è longitudinale orizzontale, cosa del tutto superflua se si trattasse di tiranti interni all'impalcato, dato che la loro azione sarebbe per forza di cose parallela alla travata. Questi tiranti definitivi invece avevano una componente longitudinale orizzontale, e un'altra perpendicolare verticale, trattasi infatti degli stralli C-O-F.
Andiamo avanti. Segue una spiegazione fra l'ovvio e l'inutile sulla funzione dei piccoli cavalletti, che come avevo già segnalato a Bandini ero stato il primo a notare, prima ancora di leggere il pdf, per la precisione in questo commento . Per poi sfociare nella banalità più assoluta:
Dunque i progettisti si erano premurati di installare quei cavi per evitare che tutta l'opera in costruzione franasse sulla sottostante ferrovia. Non l'averi mai immaginato. Proseguiamo:La funzione dei cavi pretesi provvisionali è di evitare il crollo della struttura in costruzione sulla ferrovia sottostante, visto che la travata è stata costruita senza puntellature e impalcature.
Poi hai saltato il paragrafo successivo, questo:
"Un ulteriore sistema di tiranti provvisionali, questi passanti dalla sommità dell'antenna, ha sorretto il notevole peso rappresentato dai trasversi in C ed in F, la cui funzione è quella di determinare legame statico tra l'impalcato ed i terminali dei tiranti C-O-F." (nota mia: i tiranti C-O-F sono quelli che noi stiamo chiamando stralli). Quindi qui parla di ulteriori cavi provvisionali (cioè diversi e con altra funzione rispetto a quelli citati sopra), questi vanno a costituire la futura configurazione strallata ancorandosi nei punti C ed F della travata dal punto O che è la sommità dell'antenna.
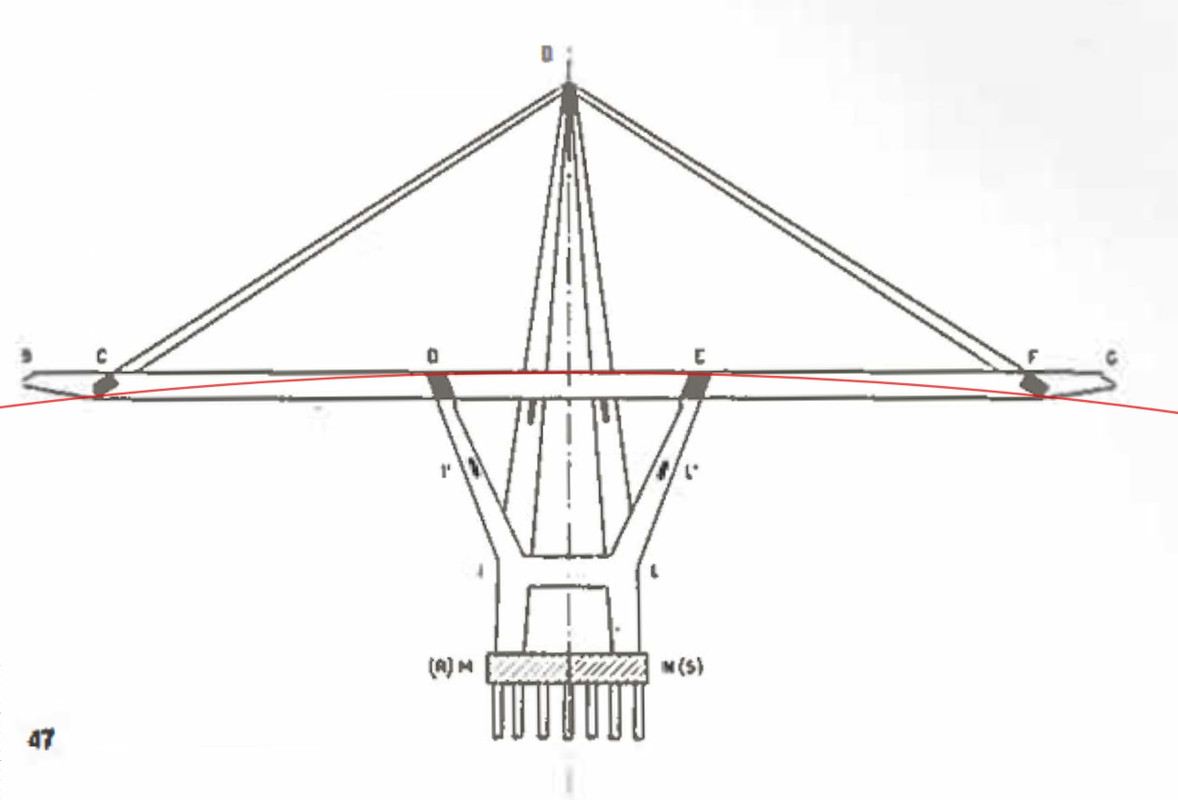
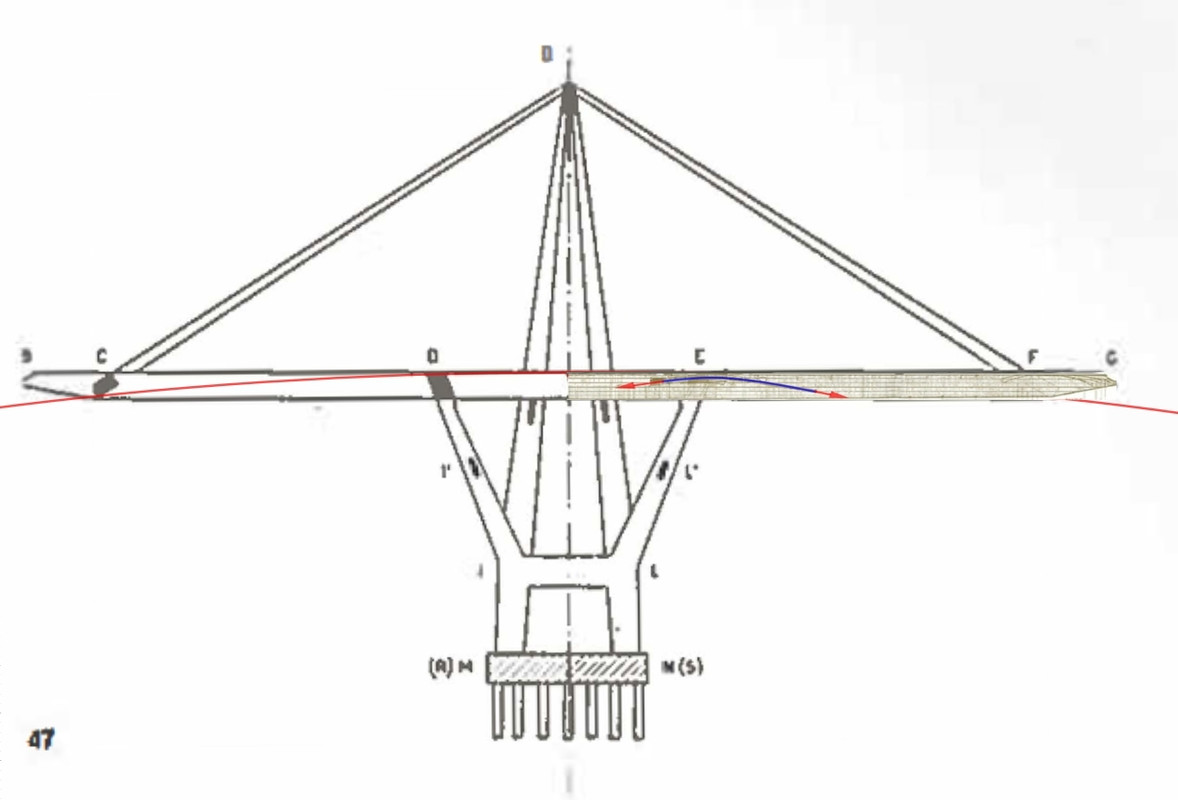
C'è un motivo se ho saltato quella parte: non era di nessuna utilità alla nostra discussione. Infatti mi riferivo a questo screenshot:
Come è evidenziato dalla didascalia, nè gli stralli definitivi nè i tiranti provvisori dalla cima dell'antenna sono ancora stati messi in opera. Come del resto i traversi in C e F, quelli dove andranno ad ancorarsi gli stralli. Qui c'è un altro momento di autosuggestione, infatti ti inventi il fatto che questi cavi provvisionali costituiscano i sostituti provvisori agli stralli definitivi, mentre il pdf dice chiaramente che la loro funzione è quella di sorreggere il notevole peso dei traversi, mentre la funzione degli stralli è affidata a tutti i tiranti provvisori, che d'altronde risultano ancora tutti tensionati al loro posto. E infatti la prova definitiva, che già ti avevo linkato ma che non hai tuttora compreso, è il seguente passo del pdf:
"Ovviamente l'operazione di trasformazione del campo tensionale interno della travata, tra il comportamento a doppio cantilever e quello a trave continua a tre luci, consistente nel montaggio e graduale messa in tensione dei tiranti C-O-F e contemporaneamente nell'altrettanto graduale asportazione di tutti i tiranti provvisori...ecc."
Abbiamo un comportamento "a doppio cantilever", quello generato da tutti i tiranti provvisori, che viene trasformato in trave continua dalla graduale messa in tensione dei soli tiranti C-O-F (gli stralli) e contestuale rilascio graduale di tutti i tiranti provvisori. Ora, quand'è che avrebbero messo in tensione gli immaginari tiranti interni all'impalcato? Non certo prima di questa fase, dato che i tiranti provvisori erano ancora tutti al loro posto. E non certo dopo, dato che la compressione alla travata C-D-E-F era già fornita dagli stralli tensionati, i quali, avendo un angolo con l'impalcato minore di 45% lavoravano prevalentemente nel ruolo di tensionatori del suddetto impalcato. Tanto più che poi il pdf ci tiene ad informarci pure di questo aspetto:
Tale operazione (la tensionatura degli stralli definitivi), controllata come già detto con opportuni sistemi geometrici e tensiometrici, è stata ogni volta eseguita senza alcun inconveniente e, al termine di essa, la travata B-G ha denunciato il comportamento di una struttura continua in cui i punti C-F erano ubicati più in alto della loro posizione definitiva (con conseguente distorsione elastica della travata) di un valore tale per cui, quando in B ed in G sono state poggiate le travate di serraglia tra due sistemi contigui, i detti punti C-F hanno occupato la posizione definitiva (con conseguente scomparsa di ogni distorsione elastica e quindi, sensibilmente, di ogni sopratensione).
Quindi, una volta tesi gli stralli definitivi, i punti terminali della travata erano un po' più in alto della loro posizione definitiva, raggiunta in seguito all'inserimento delle cerniere che completavano la campata. Anche qui nessun accenno a ulteriori tiranti definitivi diversi dagli stralli, anzi, appare evidente che tutte le operazioni di tensionatura e rilascio di tiranti dipendevano unicamente dai soli ed unici tiranti definitivi: gli stralli.
Per concludere, mi rivolgo direttamente a Bandini, o salta fuori un riferimento bibliografico che parla esplicitamente di tiranti definitivi diversi dagli stralli, oppure ti sei inventato tutto e faresti bene a chiedere scusa per avere inquinato la discussione con un mare di cazzate.
FranZη
Si prega Accesso a partecipare alla conversazione.
A pagina 2 di questo pdf:
La travata è quindi in c.a.p. e aggiungo io, del tipo post-teso, cioè la tesate sono state fatte alla fine per mezzo di martinetti idralici, un sistema illustrato nelle foto che allego"4) Una travata continua, in calcestruzzo precompresso, del tipo cellulare, con una soletta estradossale, una intradossale e 6 nervature, poggiante sul cavalletto di cui al punto 2)." www.ingenio-web.it/20925-il-viadotto-sul...dettagli-progettuali


riferimenti bibliografici:
www.federica.unina.it/ingegneria/tecnica...armato-precompresso/
www.ablaweb.net/fabriziopaolacci/documenti/c.a.p1.pdf
Alcune delle posizioni degli ancoraggi dei cavi sul ponte crollato le vedi in questa foto, altre ne troverai se le cerchi su google map.

Da ultimo, la figura 37 del pdf citato in alto, la relativa nota recita: "Armatura ordinaria e di precompressione della nervatura di una delle travi longitudinali di impalcato."

ciao
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Ti ho chiesto riferimenti bibliografici a tiranti definitivi passanti in C-D-E-F, cioè alternativi agli stralli (alla loro azione orizzontale), non riferimenti a travi in CAP in generale. Tra l'altro, dal tuo link:
I due appoggi più esterni dei quattro vincoli della travata sono costituiti dai terminali di due tiranti in acciaio pretesi che passano al di sopra di un'antenna disposta in corrispondenza dell'asse del sistema dell'altezza di 90 metri da terra e di circa 45 m sul piano viabile del ponte.
....
"agli estremi del quale, da ambo i lati del ponte, risultano assicurati due fasci di cavi che costituiscono i tiranti e scavalcano l'antenna a quota 90 metri da terra."
Ogni volta che si parla di tiranti si parla di stralli.
Quello che si vede nella foto è uno dei due punti D o E, dove l'impalcato appoggia sui cavalletti, quindi qualsiasi cosa sia quello che vedi nella foto non può essere l'ancoraggio di tiranti tesi fra C e F. Potrebbero essere i cavi pretesi fra D ed E di cui si parla a pag 14 del pdf, subito sopra la figura.Alcune delle posizioni degli ancoraggi dei cavi sul ponte crollato le vedi in questa foto, altre ne troverai se le cerchi su google map.
E quindi, data quella sezione della travata EF, quali sarebbero i tiranti passanti che vanno a tendersi in C? E quando sarebbero stati messi in tensione, dato che nel pdf vengono descritte tutte le fasi ma curiosamente si dimenticano di questa? Come si concilia questa strana omissione con la frase che ormai sto ripostando come un mantra:Da ultimo, la figura 37 del pdf citato in alto, la relativa nota recita: "Armatura ordinaria e di precompressione della nervatura di una delle travi longitudinali di impalcato."
"Ovviamente l'operazione di trasformazione del campo tensionale interno della travata, tra il comportamento a doppio cantilever e quello a trave continua a tre luci, consistente nel montaggio e graduale messa in tensione dei tiranti C-O-F e contemporaneamente nell'altrettanto graduale asportazione di tutti i tiranti provvisori..."
Come è scritto chiaramente, fino a questa fase le tre luci non si comportavano come una trave continua, ma come un doppio cantilever sostenuto dai tiranti provvisori. Una volta messi in tensione gli stralli abbiamo una trave continua a tre luci. Perchè in tutto questo si dimenticano dell'apporto al "campo tensionale interno alla travata" dato da questi ipotetici tiranti passanti per C-D-E-F? Non sarà che te li sei inventati?
FranZη
Si prega Accesso a partecipare alla conversazione.
Nella sostanza convengo con te su un aspetto: senza gli stralli il ponte non sta su.
Non ho tempo adesso di darti una risposta più argomentata su tutto quanto sopra, ma mi riprometto di farlo nel fine settimana, con qualche considerazione. Dammi il tempo. Ciao
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Questa invece la reale configurazione dei cavi, che viene a formare un "doppio cantilever sostenuto dai tiranti provvisori" in fase di costruzione, una "travata continua a tre luci" una volta che l'intero impalcato C-F viene precompresso dall'azione orizzontale degli stralli (insieme ai vincoli che questi costituiscono in C e F), con conseguente modificazione delle tensioni interne:
In definitiva, quello che era il nocciolo della questione è che l'intero impalcato non era progettato per autosostenersi senza questa azione orizzontale, ecco allora che il cedimento di uno strallo ne avrebbe evidentemente causato il collasso, a meno di non voler invocare l'intervento di San Patrizio, che mi risulta protettore degli ingegneri, magari coadiuvato da San Giovanni Battista, patrono di Genova. Quello che è certo è che non si può parlare di "ridondanza degli stralli" senza scadere nella pura fesseria. Spero con questo che dopo qualche scazzo si ritorni a discussione costruttiva, alla quale ammetto di non aver contribuito, vedrò di migliorare.
FranZη
Si prega Accesso a partecipare alla conversazione.
Morandi ha fatto un doppio calcolo:
1) configurazione doppio cantilever (doppia trave a sbalzo CD e EF collegate dal tratto intermedio DE, sorretta da cavi provvisionali e dai due cavalletti in D e E); Le armature tese del cantilever sono nella parte superiore della travata, realizzate con i cavi provvisionali
2) configurazione finale trave a tre appoggi, che essendo una trave precompressa a tre luci inflesse, è armata nella parte bassa e precompressa con i cavi post-tesi tipici della tecnologia di precompressione
Nel passaggio dalla configurazione 1 alla 2 sono stati posati stralli in C-O-F e contestualmente rimossi i cavi provvisionali C-D-E-F.
I tiranti in C-O-F realizzano una ulteriore (e fondamentale) autoprecompressione della travata tra i punti C ed F.
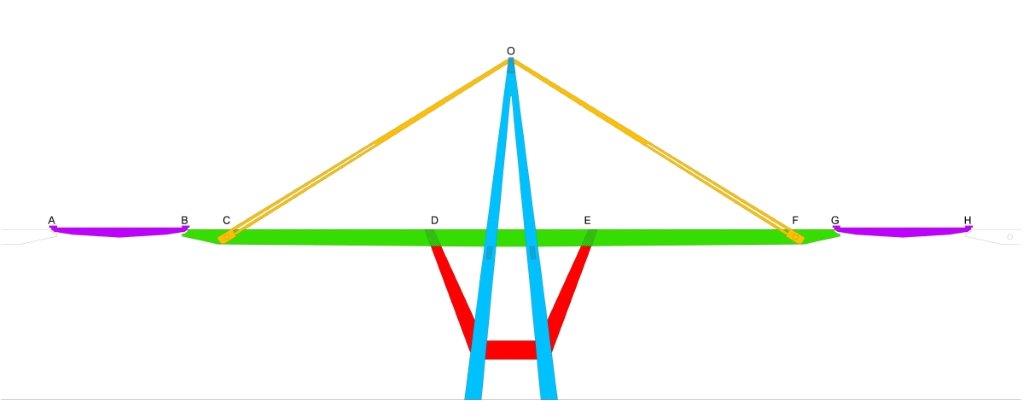
A questo punto la conclusione che mi sento di sostenere, è che l'apporto degli stralli era fondamentale per la tenuta della travata, in quanto le travi nei tratti CD e EF non erano armate per lavorare come travi a sbalzo, ma come travi inflesse. L'eventuale rottura di uno strallo o lo sganciamento o qualsiasi cosa ne avesse eventualmente causato la soppressione, dovrebbe aver prodotto un crollo relativamente rapido della travata.
Riporto qui una citazione fatta dall'utente redribbon nell'altra discussione sul crollo (#404)
Una trave inflessa ha un tipo di armatura esttamente opposto ad una trave a sbalzo."Il sistema nasce per essere fortemente compresso dagli stralli, una elevatissima compressione quasi centrata che fa lavorare in condizioni ottimali il calcestruzzo. [...] Ovviamente la soletta da ponte invece è inflessa e perciò è stata precompressa. Con questo comportamento, praticamente pendolare, il collasso di uno o più stralli porta ad una rottura complessiva rapidissima. Nessun elemento è in grado di portare le enormi flessioni ed a catena, in frazioni temporali rapidissime, cede tutto." prof. Cosenza buildingcue.it/genova-silenzio-prof-cosenza/11655/
Le travi in CD e EF non potevano tornare a lavorare come un doppio cantilever dopo la rimozione in corso d'opera dei cavi provvisionali in C-D-E-F.
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
FranZη
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Dopo la parentesi ingegneristica riprendo il normale svolgimento del thread, con un argomento leggero e solo parzialmente matematico. Penso che in molti abbiano letto il celebre racconto di Jorge Luis Borges La biblioteca di Babele, se non l'avete fatto vi consiglio di procurarvelo perchè la raccolta in cui è contenuto, Finzioni, è un classico che trovate in ogni biblioteca. Anche nella biblioteca di Babele, come vedremo. Se vi accontentate di leggerlo su uno schermo, lo trovate qui . Ecco l'inizio del racconto:
L'universo (che altri chiama la Biblioteca) si compone d'un numero indefinito, e forse infinito, di gallerie esagonali, con vasti pozzi di ventilazione nel mezzo, orlati di basse ringhiere. Da qualsiasi esagono si vedono i piani superiori e inferiori, interminabilmente. La distribuzione degli oggetti nelle gallerie è invariabile. Venti vasti scaffali, in ragione di cinque per lato, coprono tutti i lati meno due; la loro altezza, che è quella stessa di ciascun piano, non supera di molto quella d'una biblioteca normale. Il lato libero dà su un angusto corridoio che porta a un'altra galleria, identica alla prima e a tutte.
E, saltando qualche riga, la parte fondamentale:
A ciascuna parete di ciascun esagono corrispondono cinque scaffali; ciascuno scaffale contiene trentadue libri di formato uniforme; ciascun libro è di quattrocentodieci pagine; ciascuna pagina, di quaranta righe; ciascuna riga, di ottanta lettere di colore nero. Vi sono anche delle lettere sulla costola di ciascun libro; non, però, che indichino o prefigurino ciò che diranno le pagine. So che questa incoerenza, un tempo, parve misteriosa. Prima d'accennare alla soluzione (la cui scoperta, a prescindere dalle sue tragiche proiezioni, è forse il fatto capitale della storia) voglio rammentare alcuni assiomi.
La soluzione, che Borges ci offre poco dopo, è che la biblioteca contiene tutti i volumi consistenti in tutte le combinazioni dei 25 caratteri tipografici fondamentali. Dato che un volume contiene 80*40*410=1312000 caratteri, è facile calcolare il numero totale dei volumi della biblioteca: 251312000, che è circa uguale a 101834097, cioè 1 seguito dal numero di zeri dato dall'esponente. L'idea di fondo del racconto è ripresa da un' altra breve storia , La biblioteca universale di Kurd Lasswitz, il quale però (più pragmaticamente) immagina di avere a disposizione 100 caratteri tipografici, arrangiati in volumi di 500 pagine, 40 righe a pagina, 50 caratteri per riga, per un totale di un milione di caratteri a volume e 1001000000=102000000 volumi.
Ora, tornando al racconto di Borges, c'è un problema con quei "25 caratteri", unitamente ad una nota che, invece che far chiarezza, confonde ulteriormente:
1II manoscritto originale non contiene cifre né maiuscole. La punteggiatura è limitata alla virgola e al punto. Questi due segni, lo spazio, e le ventidue lettere d'alfabeto, sono i venticinque simboli sufficienti che enumera lo sconosciuto [N.d.E.].
Non è affatto chiaro quali siano queste 22 lettere, tantopiù che lo spagnolo, lingua originale del testo, annovera ufficialmente 30 lettere. Una teoria (trovata su un sito che vi indico dopo) è la seguente: dalle originali 30 lettere elimina le doppie ch, ll, rr, insieme alla ñ perchè ritenute non necessarie. Poi scarta anche la k e la w che compaiono solo in parole di origine straniera, infine la q perchè superflua e la x perchè abbreviazione di "ics". Si arriva effettivamente a 22 ma come teoria mi pare eccessivamente barocca per essere stata adottata implicitamente. Non aiuta nemmeno il fatto che uno dei volumi citati nel racconto si intitoli Axaxaxas mlö, autocitazione riferita all'altro racconto Tlön, Uqbar, Orbis Tertius, che però sfortunatamente contiene una umlaut, sicuramente incoerente col ristretto insieme di 22 lettere, più la x che teoricamente sarebbe fra le lettere eliminabili.
Risulta anche presente nell'originale l'epigrafe:
“by this art you may contemplate the variation of the 23 letters.”
...e qui le 23 lettere sembrerebbero essere quelle dell'alfabeto latino classico, al quale mancano j, u e w, ma ancora una volta ci si scontra con un'altra citazione presente nel racconto, cioè la stringa di caratteri dhcmrlchtdj che una j la contiene. Ecco che quello delle 22 lettere sembra essere un vero mistero, ciò che mi sento di dire è che non si tratta di una svista, perchè stiamo parlando di Borges e se ha concepito 22 lettere intendeva proprio dire 22. Inutile dire che la biblioteca di Babele contiene una versione di Finzioni e del nostro racconto dove la nota (1) annovera 26 lettere dell'alfabeto, togliendoci ogni dubbio. Forse, azzardo l'ipotesi, questa ambiguità o incoerenza è stata inserita appositamente per evitare che accadesse quello che poi invece è successo: qualcuno ha deciso di creare la biblioteca di Babele, nel momento in cui internet ha dato la possibilità di farlo, seppure a livello virtuale. Il sito libraryofbabel.info costituisce il primo tentativo di generare una biblioteca di Babele, anche se incompleta (ma completabile, in linea di principio).
Funziona così: scegliete una sala esagonale inserendo una sequenza alfanumerica di massimo 3260 caratteri (questa limitazione, del tutto inessenziale dal punto di vista pratico, comporta però che concettualmente questa non sia una vera biblioteca di Babele ma solo una parte). Scegliete ora il muro, lo scaffale e infine il libro. Io per esempio ho scelto questo:
Si intitola ua efyobas e inizia con:
dosqorgpztj jzihmzg.mhomevdjfb,laxshvjwcsramzyvetupywzzw.qj,nktzrdutktalrocuogoq
.pkcubxv,lkjfjweuuqhje,,ppjii,vemywgzsuwl fsuswpw fximwpq,stbanopyxk,uccabyl.ord
lun.k,elmcatgxiebglxp.stndix ctlfacdjuv.ggoyi araojlebyyuchoyetius,yflgljd ayncv
orpgx..
Ovviamente in questa replica virtuale della biblioteca di Babele hanno deciso di tagliare la testa al toro, usando tutte le 26 lettere dell'alfabeto più i tre segni di punteggiatura e spazio vuoto, portando così a 291312000 il numero possibile di combinazioni (e quindi volumi), vale a dire 101918666 circa. Gli scaffali per sala sono passati da 5 a 4, seguendo una successiva correzione dello stesso Borges, per un totale di 4*5*32=640 volumi per sala (nella versione originale, con una scaffalatura in più, erano 800). Questo, considerata la limitazione del numero di sale esagonali già accennata sopra, comporta per la biblioteca virtuale un totale di volumi di circa 105076, molti meno di quelli della biblioteca originale, come detto, però molti più di quelli effettivamente necessari, dato che questi volumi sono solo potenziali, finchè qualcuno non va a consultarli effettivamente, come ho fatto io. Una specie di applicazione bibliotecaria della meccanica quantistica, che sicuramente avrebbe gradito Borges, vediamo come funziona.
Come detto si sceglie dapprima una sala, poi un muro, poi uno scaffale. A questo punto inizierete a poter leggere i titoli sulle costole dei libri dello scaffale, è avvenuta quindi la prima generazione di stringhe casuali da parte del computer, l'equivalente del collasso di una funzione d'onda quantistica. In pratica, finchè nessuno aveva osservato ancora lo scaffale, questo potenzialmente conteneva 32 volumi aventi per titolo delle stringhe qualsiasi di caratteri, nel momento in cui il primo occhio umano (presumibilmente proprio il mio) ha avuto modo di leggere quei titoli, ecco che questi sono fissati per sempre. Ovviamente sempre se l'algoritmo che genera la biblioteca è implementato correttamente. Quindi se ora voi andate a consultare lo stesso scaffale troverete gli stessi libri, e se aprite ua efyobas a pag.1 troverete la stessa sequenza di simboli. Tra l'altro il volume è ancora quasi tutto potenziale, visto che ho sfogliato solo la prima pagina più altre due o tre a caso. E ovviamente l'ultima. A questo proposito, vi saluto con le ultime parole del libro:
amvynije,biogrika cc.mzu.f
FranZη
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Inizio con questo post una nuova saga che ha come protagonista il noto personaggio Odifreddi, non tanto perchè sentivo di aggiungere qualcosa a quanto già scritto qui , ma perchè mi è stato recentemente regalato il suo libro Il vangelo secondo la scienza, credo sia il primo che ha scritto, e leggendolo di vaccate ne ho trovate davvero parecchie, ecco che allora ho pensato di dover estrarre del materiale per questo thread.
Come ci spiega lo stesso autore nell'introduzione, il libro avrebbe dovuto intitolarsi nelle sue intenzioni Dalla Galilea a Galileo, titolo che però non piacque all'editore. Quanto al contenuto, a parte una critica poco equilibrata alla religiosità in generale (non solo quella cattolica o cristiana), si tratta più che altro di un excursus dei classici argomenti scientifici da divulgazione, in quest'ambito il miglior testo mai scritto è La mente nuova dell'imperatore di Roger Penrose e il libricino di Odifreddi non meriterebbe nemmeno di essere sfogliato, figuriamoci acquistato; ma la parte interessante è la sua tesi di fondo, che lui stesso riassume così:
La vera religione è la matematica, il resto è superstizione.
Solo che, invece che essere presentata come opinione personale, la precedente affermazione ha la pretesa di essere il risultato di secoli di ricerca scientifica, o più precisamente della parte divulgativa del libro, che in questo modo si vorrebbe omnicomprensiva delle tematiche scientifiche pertinenti all'argomento. A mio avviso la tesi di Odifreddi si può però riassumere più correttamente con quest'altra citazione, sempre letterale dal testo:
O si è logici o si è patologici!
Siccome Odifreddi stabilisce a priori un'equivalenza fra logica ed ateismo, ecco che ogni forma di non-ateismo diventa nel suo pensiero patologia. Infatti interpreta la congiunzione "o" in senso esclusivo - e qui non si dimostra logico - sebbene la logica stessa sia prodiga di controesempi, tanto che Alfred Tarski sosteneva ironico di essere il più grande logico vivente, fra quelli non matti. Con ciò sottointendeva che il più grande fra quelli matti, e fra tutti i logici viventi, era certamente Gödel, uno che aveva pure prodotto una prova dell'esistenza di Dio, prova che il nostro Odifreddi non mancherà di analizzare nel suo libro, ma questo sarà argomento di un'altra puntata.
Singolare poi la coincidenza onomastica: umlaut a parte, Gödel è la fusione di God ed El, il Dio degli inglesi e quello degli ebrei, senza voler entrare nel campo della semantica e nelle traduzioni letterali di Mauro Biglino (che peraltro apprezzo).
Veniamo ora all'estratto che vorrei commentare, che invece riguarda esclusivamente la logica formale, nella quale Odifreddi dovrebbe essere maestro, non fosse altro per il fatto che la insegna all'università.
Ecco dunque il nostro estratto, preciso subito che la foto l'ho aggiunta io più che altro per non avere eventuali problemi di diritti d'autore per aver citato un passo troppo lungo. Nel caso dovrebbe fare a metà con gli eredi di Borges dato che il cinquanta per cento del testo scansionato (la metà intelligente) è rubato a lui. Dico "rubato" perchè sono abbastanza sicuro che non avrebbe per nulla apprezzato l'argomentazione (il)logica che Odifreddi gli fa seguire.
Veniamo subito all'illogicità, così che nessuno possa pensare che il mio giudizio sia diffamatorio. Il primo matematico a dare una definizione assiomatica dei numeri naturali fu il grande logico Giuseppe Peano, che per combinazione studiò e insegnò nella stessa università di Torino di Odifreddi, ma questo successe un secolo prima che il secondo (infinitamente meno grande) logico arrivasse sulla scena. Prima di Peano era diffusa fra i matematici la tesi di Kronecker, secondo la quale "i numeri naturali sono opera del buon Dio", roba che se fosse in voga oggi Odifreddi ci scriverebbe una collana di volumi. Peano mise giù cinque assiomi facili facili che permettono di definire i numeri naturali, vale la pena di citarli:
- Esiste un numero naturale, denotato 0.
- Ogni numero naturale ha un numero naturale successore.
- Numeri diversi hanno successori diversi.
- 0 non è il successore di alcun numero naturale.
- Ogni sottoinsieme di numeri naturali che contenga lo zero e il successore di ogni proprio elemento coincide con l'intero insieme dei numeri naturali (assioma dell'induzione).
La teoria che segue dagli assiomi 1-5 è la teoria dei numeri naturali del secondo ordine. Non ha molta importanza ora spiegare cosa significhi quest'ultima specificazione sull'ordine, ci basti sapere che questa è la versione originale (e definitiva) dell'assiomatizzazione dei numeri naturali, e che come dimostrò lo stesso Peano si tratta di una teoria categorica, o monomorfa, che sono termini tecnici per indicare il fatto che ogni struttura matematica che verifica i cinque assiomi è la stessa struttura a meno di differenti notazioni. Cioè i numeri naturali sono sempre e solo quelli, a prescindere dal modo in cui decidiamo di chiamarli, per esempio usando cifre arabe o romane o egizie non si modifica la struttura dei numeri naturali.
Quindi cosa c'entrano questi modelli non standard di cui parla Odifreddi? In realtà nulla, per almeno due ordini di ragioni. Prima ragione: come già detto gli assiomi di Peano definiscono un'unica struttura, i modelli non standard si costruiscono a partire da un'altra assiomatizzazione dei numeri naturali, che prende il nome di Aritmetica di Peano. Si tratta della versione "al prim'ordine" degli assiomi presentati prima, la più evidente differenza è che in questo caso servono infiniti assiomi per tradurre quelli originali di Peano, ecco allora che per confutare l'esistenza di Dio Odifreddi è costretto ad accettare l'esistenza attuale di un'infinità di clausole, e già qui potrebbe sorgere il sospetto che solo una mente infinita avebbe la possibilità controllarle tutte. Ma soprattutto non si capisce perchè la logica dei predicati del secondo ordine, cioè quella in cui Peano ha ambientato il suo lavoro, vada rigettata a priori, se non appunto per riuscire a controbattere alla prova ornitologica di Borges.
Seconda ragione, più tecnica e se vogliamo errore ancora più grave visto che a commetterlo è un ordinario di logica: nei modelli non standard dell'aritmetica di Peano non c'è comunque nessun numero naturale indefinito compreso fra 0 e 10, o fra 0 e 10 miliardi di miliardi, e così via. I nuovi numeri naturali che compaiono in questi modelli non standard sono da interpretarsi come numeri infiniti, maggiori di ogni altro numero naturale definito dagli assiomi di Peano. Quindi la prova ornitologica, per quanto faceta, resiste senza scalfiture alle bordate di Odifreddi. Quella che viene travolta a palle incatenate è invece proprio l'inferenza finale del nostro eroe:
"Se qualche numero è indefinito, come appunto succede negli universi non standard, allora Dio non esiste."
Siccome questi numeri indefiniti abbiamo appena visto che sono da considerarsi anche infiniti, perchè il ragionamento di Borges cada bisogna aggiungere nelle premesse che lo stormo di uccelli immaginato sia infinito (altro grave errore per un logico aggiungere ipotesi implicite senza segnalarlo). Qui abbiamo un altro infinito attuale, questa volta prodotto direttamente dalla mente di Borges. Ma quale mente umana può visualizzare un infinito attuale? Seguendo il ragionamento di Odifreddi bisogna concludere che se il numero di uccelli immaginato da Borges è indefinito, allora Borges è Dio. Ora, possiamo essere abbastanza sicuri del fatto che Borges non sia Dio, per quanto lo ammiri come scrittore, quindi è falsa la premessa, ossia che il numero di uccelli immaginato sia indefinito, e con ciò la controargomentazione di Odifreddi viene disalberata e lasciata impotente a vagare senza meta nel mare delle illogicità le quali, lo ricordo, secondo lo stesso Odifreddi-pensiero sono da considerarsi come patologie.
FranZη
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Rinserratevi con qualche amico nella maggior stanza che sia sotto coperta di alcun
gran navilio, e quivi fate di aver mosche, farfalle e simili animaletti volanti; siavi
anche un gran vaso d’ acqua, e dentrovi dei pescetti, sospendasi anco in alto qualche
secchiello, che a goccia a goccia vadia versando dell’ acqua in un altro vaso di
angusta bocca, che sia posto in basso: e stando ferma la nave, osservate diligentemente
come quelli animaletti volanti con pari velocità vanno verso tutte le parti della stanza,
e i pesci si vedranno andar notando indifferentemente per tutti i versi; le stille cadenti
entreranno tutte nel vaso sottoposto; e voi, gettando all’ amico alcun cosa, non più
gagliardamente la dovrete gettare verso quella parte che verso questa, quando le
lontananze sieno uguali, e saltando voi, come si dice, a piè giunti, egual spazii
passerete verso tutte le parti.
Osservate che avrete diligentemente tutte queste cose, benchè niuno dubbio vi sia che
mentre il vassello sta fermo non debbano succedere così; fate muovere la nave con
quanta si voglia velocità: ché (pur che il moto sia uniforme e non fluttuante in qua e in
là) voi non riconoscerete una minima mutazione in tutti li nominati effetti, né da alcuno
di quelli potrete comprendere se la nave cammina oppur sta ferma...
Galileo Galilei, Dialogo sopra i due massimi sistemi del mondo
Con questo noto esperimento ideale, nonché con la sua formidabile prosa scientifica, Galileo spiegava al mondo il suo Principio di Relatività, oggi meglio conosciuto come prima legge di Newton e riassunto nella forma:
In assenza di forze ciascun corpo persevera nel suo stato di quiete o di moto rettilineo uniforme.
La cosa, per quanto ci appaia scontata dopo secoli di abitudine ad enunciare il principio, scontata non è affatto, dato che nel nostro mondo è una situazione che praticamente non si verifica mai. In primis perchè nel nostro universo non esistono luoghi in cui ci sia una reale e totale assenza di forze. In secondo luogo, anche se tecnicamente è un caso particolare della prima affermazione, perchè qui sulla terra ci sono sempre degli attriti a deviare, rallentare e infine arrestare il moto dei corpi che vorrebbero proseguire indefinitamente nel loro incedere uniforme. La grande idea di Galileo è stata quella di astrarre i fenomeni reali e ragionare su quelli ideali (benchè l’esperimento del “gran navilio” appaia reale, non è però molto realistico…). Grazie a questa intuizione riuscì ad individuare le prime leggi della Fisica moderna, come per esempio quella ben nota sulla caduta dei gravi, superando così i limiti della Fisica aristotelica. Altro esempio, tra parentesi, di esperimento che nel mondo reale è piuttosto complesso da realizzare: servono un tubo sottovuoto abbastanza grande da contenere la classica piuma e martello...l’esperimento della Torre di Pisa è invece proprio un falso storico.
Ma qui non intendo parlare di Galileo, quanto delle trasformazioni che portano il suo nome. Sono la traduzione matematica del suo principio di relatività e hanno la forma seguente:
Sono le equazioni sulla destra, già accoppiate a delle altre omologhe che ci serviranno fra breve. Regolano il cambiamento di coordinate fra due sistemi inerziali inizialmente coincidenti, il secondo dei quali li muove rispetto al primo con velocità costante v lungo la direzione positiva dell'asse delle x (nel disegno v è indicata con v0):
Vediamo innanzitutto di spiegare cosa significano. Le quattro coordinate (x,y,z,t) sono le usuali tre coordinate spaziali più il tempo rispetto ad un certo sistema di riferimento che chiamiamo S. Quando sostituiamo dei numeri alle variabili abbiamo le coordinate spazio-temporali di un evento, cioè un dato luogo in un dato tempo.
Per esempio, supponiamo di avere un sistema di riferimento S centrato su casa mia, con gli assi x e y in direzione rispettivamente nord e ovest, diciamo che io esco di casa per dirigermi in un punto a 1.414 Km in direzione nord-ovest cronometrando il tempo impiegato. Quando faccio partire il cronometro le mie coordinate spazio-temporali sono (0,0,0,0), se impiego 5 minuti a percorrere il tragitto, una volta arrivato le mie coordinate saranno (1000,1000,0,300), misurate in metri e secondi. Notare che essendo z=0, ho supposto implicitamente che il punto d'arrivo sia esattamente alla stessa quota della mia abitazione, dato che la coordinata z è la verticale sul terreno. Dovrebbe anche essere chiaro perchè ho scelto quel numero particolare per la distanza del punto finale, in effetti per la precisione avrei dovuto scrivere "radice di due Km" per avere delle coordinate intere per il secondo evento.
Se adesso è chiaro cos'è un evento e come si individua, facciamo un altro passettino nella direzione della spiegazione delle equazioni di Galileo: immaginiamo che nell'istante in cui esco di casa sopra la mia testa stia passando un aereo, alla quota di 10000 metri, che vola in direzione nord alla velocità costante di 200 metri al secondo. Prendiamo questo aereo come nuovo sistema di riferimento, che chiameremo S', le cui coordinate spazio-temporali sono espresse dalle variabili accentate (x',y',z',t'). Le equazioni di Galileo servono per stabilire quale sia il corretto passaggio di coordinate fra i due sistemi. L'evento 1, io che esco di casa, avrà infatti nel sistema S' le coordinate (0,0,-10000,0), mentre l'evento 2, io che arrivo a destinazione, avrà coordinate (-59000,1000,-10000,300). Ora, la terza coordinata è la quota – costante - dell'aereo, e in effetti non è contemplata dalle equazioni riportate sopra (c'è scritto z'=z...), questo perchè i due sistemi erano supposti inizialmente coincidenti. Però avendo fatto l'esempio di un aereo non potevo supporre che volasse rasoterra. Ho sacrificato un briciolo di semplicità al realismo. Mi sembra però piuttosto ovvio il significato della coordinata z in questo esempio, perciò non parliamone più e concentriamoci sulle altre tre. Come si vede, le coordinate y' e t' sono uguali nei due sistemi di riferimento, mentre la x’ è variata, in accordo con le equazioni di Galileo, per via del fatto che durante il mio tragitto l'aereo si è spostato di un bel po' in direzione nord, per la precisione di 60 km, ed ecco quindi che al mio arrivo mi trovo 59 km alle sue spalle.
La relatività galileiana afferma che le leggi della Fisica sono invarianti per trasformazioni di Galileo, vale a dire che presa una qualunque legge espressa sotto forma di equazione nelle variabili spazio-temporali (x,y,z,t) di un sistema di riferimento inerziale S, questa resta invariata quando espressa rispetto alle variabili (x',y',z',t') di un altro sistema inerziale S'. Per esempio la famosa seconda legge di Newton F=m*a è invariante per trasformazioni di Galileo. Tutto questo è molto bello, è anche molto utile nella stragrande maggioranza delle applicazioni pratiche, però purtroppo è falso nell'universo in cui viviamo. Sia chiaro un punto: a livello astratto, matematico, la relatività galileiana è un assioma della Fisica classica, perciò tutto quello che ne deriva è logicamente corretto e consistente con tale assioma. Quello che è sbagliato è che certe leggi della natura non vogliono essere invarianti rispetto alle trasformazioni di Galileo, ma essendo sperimentalmente riconosciute come legittime leggi della Fisica, questo comporta che ad essere illegittime siano proprio le trasformazioni di Galileo.
Questi problemi di mancata invarianza cominciano a palesarsi con le equazioni di Maxwell , che regolano i fenomeni elettromagnetici. E' infatti noto dalla fine dell'800 che queste equazioni non sono invarianti rispetto alle trasformazioni di Galileo, bensì rispetto ad un altro gruppo di trasformazioni dette di Lorentz, che sono quelle riportate qui sopra accanto alle trasformazioni di Galileo. Come si vede interviene un nuovo parametro, la velocità della luce c, il cui valore è notoriamente di circa 300000 Km al secondo, o usando la notazione esponenziale 3*108 m/s. Dato che la velocità della luce è molto molto grande, normalmente si avrà che la velocità v del sistema di riferimento S' è molto piccola in rapporto, perciò tanto le quantità v/c2 quanto v2/c saranno prossime a 0. Nel nostro esempio dell'aereo sono per esempio:
v/c2=6.67*10-15
v2/c2=1.33*10-12
ossia due numeri nell'ordine dei milionesimi e millesimi di miliardo rispettivamente. Se sostituiamo nelle trasformazioni di Lorentz queste due quantità con 0, il che comporta un'approssimazione minima, otteniamo precisamente le trasformazioni di Galileo. Un modo equivalente di vedere la cosa è affermare che le trasformazioni di Galileo sono il caso limite delle trasformazioni di Lorentz quando la velocità della luce c tende a infinito. La soluzione al problema delle equazioni che non risultano Galileo-invarianti è dunque questa: le trasformazioni "giuste" della Fisica sono quelle di Lorentz, solo che in tutti quei fenomeni che comportano velocità ordinarie, cioè non confrontabili con la velocità della luce, queste si riducono praticamente alle trasformazioni di Galileo.
Con un celebre articolo del 1905 A. Einstein fu il primo a sostituire questo "assioma di Lorentz" al precedente "assioma di Galileo" come base dei fenomeni fisici, unitamente a un altro assioma assai sconvolgente eppure rilevato sperimentalmente: quello che stabilisce che la velocità della luce nel vuoto è sempre la stessa, indipendentemente dal moto dell'osservatore. Questo è il vero contributo di Einstein alla Relatività Speciale (è la teoria che segue dalle trasformazioni di Lorentz), sebbene spesso gli si attribuisca tutto il merito. Invece il credito per la successiva teoria della Relatività Generale va giustamente quasi tutto a lui, ma non ce ne occuperemo qui. Per quanto riguarda la Relatività Speciale, o Ristretta, i risultati fondamentali erano già noti prima dell'articolo di Einstein, ovviamente un ruolo lo aveva avuto anche il fisico olandese H.A.Lorentz, ma sostanzialmente i risultati di Einstein erano stati già ottenuti tutti dal grande matematico francese J.H.Poincaré qualche anno prima, con la non irrilevante differenza che Poincaré non aveva ritenuto di dover cambiare le leggi della fisica classica in base ai nuovi risultati matematici, ma piuttosto che fossero i risultati matematici a dover essere meglio raccordati con la natura.
In ogni caso il vero eroe della relatività ristretta è il matematico Hermann Minkowski, che nel 1907 dette una elegante sistemazione alla teoria, che sostanzialmente è quella ancora oggi accettata, e senza la quale non avrebbe potuto essere elaborata nessuna Relatività Generale. L'idea di Minkowski possedeva la caratteristica fondamentale delle idee geniali: la semplicità. Fino a quel momento la Fisica si basava sulla concezione di uno spazio tridimensionale euclideo, più una variabile separata e assoluta, il tempo. Minkowski in luogo di inserire le nuove leggi di trasformazione delle coordinate, con tutte le conseguenze che comportavano, in questo quadro classico, pensò di modificare direttamente il quadro di riferimento di base, postulando che la vera geometria del nostro universo non è quella euclidea, bensì quella definita dalle trasformazioni di Lorentz stesse, ossia uno spazio quadridimensionale nel quale il tempo ha lo stesso ruolo dello spazio, e in particolare dipende dalla velocità dell'osservatore.
Per giungere a questa visione rivoluzionaria si appoggiò a precedenti concezioni, squisitamente matematiche, elaborate una trentina di anni prima da un altro matematico tedesco, Felix Klein. Infatti, in seguito alla scoperta delle geometrie non euclidee avvenute nella prima parte dell'800, per un certo periodo ci fu un po' di confusione circa cosa dovesse intendersi realmente con "geometria". Per almeno due millenni geometria era stata sinonimo di geometria euclidea, tanto per dire: nella sua Critica della ragion pura Kant la considerava semplicemente sintetica a priori, una necessità insomma. Poi, appunto, le geometrie non euclidee, e infine, nel 1872, il Programma di Erlangen di Klein, col quale ridefiniva completamente il concetto di geometria. Per Klein, con il termine "geometria", andava inteso un qualsiasi spazio dotato di leggi di trasformazione delle coordinate, che in sostanza servono per stabilire cosa deve essere considerato equivalente e cosa no in quel particolare tipo di geometria. Con ciò la geometria euclidea diventava dunque solo una delle infinite possibili. La geometria di Minkowski era un'altra possibilità, che a quanto pare si accordava meglio con la realtà fisica.
Per definire una particolare geometria si fa uso del concetto di distanza, o metrica, semplicemente ponendo come assioma della nostra geometria in quale modo vada misurata la distanza fra due punti. E' in realtà sufficiente definire la distanza di un generico punto dall'origine, per esempio nello spazio tridimensionale euclideo la distanza s è definita da:
s2=x2+y2+z2
Non è altro che' il teorema di Pitagora in tre dimensioni anzichè due. In effetti tale teorema vale solo negli spazi euclidei. Normalmente si usa la notazione differenziale per definire la metrica:
ds2=dx2+dy2+dz2
che sta a indicare che stiamo parlando della distanza fra due punti infinitamente vicini. Nello spazio di Minkowski la metrica è definita invece da:
ds2=dx2+dy2+dz2-c2dt2
Si noti che, mentre nella metrica euclidea esiste un solo punto per cui ds=0, cioè l'origine O=(0,0,0), nello spazio di Minkowski ponendo ds=0 si ottiene:
dx2+dy2+dz2 = c2dt2
che è l'equazione di un cono (di dimensione 3...) centrato nell'origine, mentre la costante c2 fa sì che il cono sia molto aperto, nelle usuali unità di misura di metri e secondi. Il cono rappresenta il fascio di luce emesso da una sorgente situata nell'origine all'stante t=0, che si espande appunto nello spazio quadridimensionale, per quanto riguarda la falda superiore, quella inferiore è invece la luce che raggiunge l’osservatore sempre nell’istante t=0. Rinunciando a una coordinata spaziale possiamo visualizzare la situazione:
La falda superiore del cono è perciò la luce che si propaga verso il futuro, la falda inferiore è invece la luce emessa da sorgenti nell'universo e che viene captata dall'osservatore nell'istante t=0 (quindi in sostanza, se torniamo in quattro dimensioni, la falda inferiore è l'universo come lo possiamo osservare dal punto (0,0,0,0)). Il moto dell'osservatore influenza le posizioni relative di tutti gli eventi dello spazio-tempo, qui un'animazione che illustra cosa succede (rinunciando stavolta a due dimensioni spaziali...):
Se tutto ciò che sta dentro al cono è il passato e il futuro, il presente dove sta? Evidentemente sta fuori dal cono, in particolare l’iperpiano di equazione t=0 rappresenta lo spazio contemporaneo (sempre riferito al nostro osservatore iniziale), mentre tutto il resto di spazio esterno è una sorta di limbo, inaccessibile al nostro osservatore, di eventi che hanno coordinate di tipo spazio (per usare la terminologia coniata da Minkowski e oggi di uso comune).
L’iperpiano dello spazio contemporaneo (ragionando come prima in due dimensioni ci troviamo con un normale piano geometrico, ed è il piano con le stelle disegnate nell'immagine sopra, tuttavia sarebbe ancora definito dall’equazione t=0, ecco perché per i matematici ragionare in dimensione n>3 non è un gran problema…) ha un ruolo speciale nello spazio esterno all cono di luce per via del fatto che separa il passato dal futuro. Ma attenzione: solo per il nostro osservatore particolare, un altro osservatore avrà in generale un diverso iperpiano dello spazio contemporaneo e perciò, incredibili dictu, una diversa opinione sulla successione cronologica degli eventi. Ossia: se per l’osservatore O l’evento A è precedente a B, potrebbe darsi che per un altro osservatore O’ sia l’esatto contrario! Fortunatamente questo può solo avvenire per eventi A e B incorrelati, cioè tali che ciascuno dei due stia fuori dal cono di luce centrato nell’altro, insomma tali che non possano essere “messi in contatto” se non da segnali più veloci della luce, che per quanto ne sappiamo non esistono.
A questo punto in una normale esposizione divulgativa della Relatività si comincerebbe a parlare di gemelli, paradossi temporali e cose simili. Io non ho intenzione di fare nulla di tutto ciò, perché in effetti il mio intento, fin dall’inizio, era un altro, e cioè portare l’attenzione su un fatto piuttosto curioso dello spazio-tempo di Minkowski, che normalmente passa inosservato. C’è in realtà un motivo se nessuno o quasi ne parla: il motivo si chiama Relatività Generale. Quello che sto per farvi notare infatti è un aspetto peculiare della Relatività Speciale che svanisce quando si generalizza la teoria a spazi curvi.
Riprendiamo la definizione di metrica (= distanza) di Minkowski:
ds2=dx2+dy2+dz2-c2dt2
con un trucchetto matematico possiamo scriverla anche così:
ds2=dx2+dy2+dz2+(icdt)2
dove i è l’unità immaginaria, cioè la radice quadrata di -1 (ne ho già parlato su questo forum qui e qui ). Quindi la metrica di Minkowski si riduce alla usuale metrica euclidea a patto di considerare il tempo come una quantità immaginaria! Non è straordinario tutto ciò? Non solo. Questo punto di vista ci porta anche a riconsiderare le altre due grandezze fondamentali della cinematica: velocità e accelerazione. Infatti essendo per definizione rispettivamente:
v=ds/dt
a=d2s/dt2
risulta che la velocità è da considerarsi anch’essa una quantità immaginaria, mentre l’accelerazione torna ad essere una grandezza reale. Inoltre, essendo 1/i=i/i2=-i e 1/i2=-1, entrambe risultano di segno opposto rispetto alle grandezze da cui sono ricavate, cioè la velocità sarebbe da intendersi come un “tempo al contrario” e l’accelerazione come uno “spazio al contrario”. E per finire una forza, che è un’accelerazione moltiplicata per una massa, diventerebbe una sorta di “massa negativa”. Mica male come spunto di riflessione, no?
FranZη
Si prega Accesso a partecipare alla conversazione.
- gino sighicelli
-
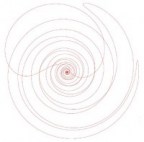
- Offline
- Utente bloccato
-
- Messaggi: 31
- Ringraziamenti ricevuti 21
ma non credo sia questa la soluzione più plausibile
sono molto più propenso a considerare plausibilmente valida un’ipotesi molto più astratta (una soluzione molto più generalizzabile)
in fin dei conti, Borges la chiamò “L'universo (che altri chiama la Biblioteca)”. Pertanto, la soluzione escogitata dovrebbe necessariamente essere stata una soluzione ‘universale’: non credo Borges fosse talmente ingenuo da limitarsi all’intendimento di un ‘universo’ valido solamente per chi parli lo spagnolo (o un qualsiasi altro particolare linguaggio umano)
l’universo di Borges doveva necessariamente includere qualsiasi opera pubblicabile – indipendentemente dalla lingua utilizzabile
la soluzione più plausibile a mio parere la si trova partendo dalla comprensione di quanto fu enorme la conquista realizzata, circa tre millenni fa, mediante l’invenzione della tecnica alfabetica
la tecnica alfabetica in pratica altro non fu che la scoperta di quanto fossero stati 'stupidi' gli individui delle generazioni precedenti; essendo stato per essi molto più che duplice lo sforzo mnemonico richiesto, rispetto a chi altrimenti abbia a dover utilizzare solamente il linguaggio parlato normalmente
la tecnica alfabetica consistette nella riproduzione approssimativa del linguaggio parlato mediante la trascrizione di un relativamente piccolo insieme dei suoi fonemi, tra quelli in esso normalmente utilizzati
ciascun popolo utilizza un proprio linguaggio, a sua volta fondato su un qualche particolare insieme di fonemi. Normalmente i fonemi utilizzati in un linguaggio sono molto più numerosi dei simboli fonetici successivamente (e convenzionalmente) utilizzati nella trascrizione di quello stesso linguaggio
ad esempio, nel caso dell’italiano i fonemi convenzionalmente corrispondenti ai simboli utilizzati sono sicuramente meno di 21 (nell’italiano non toscano, la lettera ‘h’ viene infatti considerata ‘muta’; mentre peraltro la lettera ‘q’ risulta essere pressoché inutile)
i fonemi che formano l’italiano sono peraltro molto più di 21: alcuni fonemi vengono approssimati mediante combinazioni di lettere e accenti (ad esempio: ò, à, ì, ù, è, é); altri vengono approssimati mediante combinazioni di due lettere (ad esempio: il fonema ‘sc’ di “sci”; il fonema ‘c’ di “ci”; … );
nonostante i fonemi realmente utilizzati siano molto più numerosi di quelli convenzionalmente utilizzati nella sua trascrizione, gli utilizzatori del linguaggio italiano riescono comunque ad apprendere la tecnica della sua trascrizione, e senza uno sforzo affatto straordinario, normalmente tra il quinto ed il sesto anno di età, ed in modo tale da poter poi riprodurre una conversazione per il tramite della lettura di una sua trascrizione; e ciò in una età in cui la fase di maggiore plasticità del cervello umano è oramai pressoché terminata (la lateralizzazione dei centri linguistici dei nostri cervelli (area di Broca ed area di Wernicke) normalmente avviene entro il terzo anno di età – nell’intervallo di tempo in cui avviene la lateralizzazione, le capacità linguistiche possono svilupparsi pressoché in automatico (quasi senza richiedere alcuno sforzo mnemonico e/o di concentrazione); nel caso l’acquisizione del linguaggio avvenga in epoca più tarda, tanto più essa sarà stata tarda tanto meno risulterà essere stata soddisfacente l’acquisizione linguistica realizzata (rispetto allo standard), ed al contempo tanto più gravoso l’impegno che a tal fine sarò stato richiesto
è pertanto che sono propenso a considerare molto più plausibile l’ipotesi che nell’universo di Borges i 22 simboli debbano essere considerati relativi ai 22 principali fonemi di ciascun linguaggio umano possibile (nel presente nel passato e nel futuro)
forse Borges non la pensò nello stesso identico modo in cui la penso anch’io; eppure credo la pensò in modo molto simile a come anch’io la penso (oppure, se lo si vuole, ciò lo si può esprimere in altro, ma 'sostanzialmente' poco differente modo: io probabilmente la penso in modo molto simile a come io ipotizzo che anche Borges pensò la questione della tecnica alfabetica)
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Dato che la biblioteca è l'universo, quel 22 potrebbe essere riferito al numero di cromosomi umani (esclusi i cromosomi sessuali X e Y), se non fosse per il particolare che il racconto è stato pubblicato prima della scoperta del numero dei cromosomi umani. Altra ipotesi: 22 nel sistema binario si scrive 10110, se poniamo 1=="-" e 0=="." del codice Morse, 10110 si legge "TETTE". Che sia questa la soluzione?
FranZη
Si prega Accesso a partecipare alla conversazione.