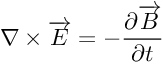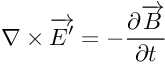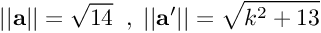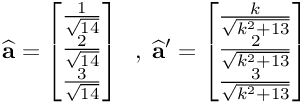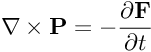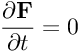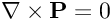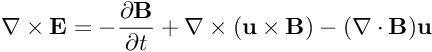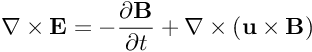La formula del latte è Vacca2O

FranZeta ha scritto: Quello che sto per farvi notare infatti è un aspetto peculiare della Relatività Speciale che svanisce quando si generalizza la teoria a spazi curvi.

Interessante. Che altro potresti aggiungere a proposito?
Nella risposta tieni conto che io sono esperto di entrambe, mi interessa l'aspetto più propriamente matematico.
Secondo me Einstein si era accorto benissimo dei limiti e delle incongruenze della RS ed è per questo che ha sviluppato la RG.

probabilmente abbrevia troppo

un fatto è che risposi al volo: mi accorsi di quella discussione nel mentre mi stavo approssimando alla parte in cui invece discutevi i sistemi di riferimento inerziali

un altro fatto è che qualcosa bisogna pur sempre (e necessariamente) tralasciare, poiché altrimenti qualsiasi discussione diverrebbe troppo ampollosa

dunque di seguito non mi preoccuperò di non essere noioso ...

un ultimo ulteriore fatto è che proprio non sostenni la tesi che « 22 è da riferirsi ai "principali fonemi umani" (passati presenti e futuri!!!) »

infatti ritenni di avere implicitamente affermato che 19 o 21 o 22 o 26 fa poca differenza; poiché in ogni caso una qualsiasi normale tecnica di trascrizione di un linguaggio umano è necessariamente approssimativa (ad esempio, rispetto ad una sufficientemente fedele registrazione audio)

avevo infatti accennato il fatto che ogni linguaggio umano è composto di un particolare insieme di fonemi

peraltro, i segni utilizzati non sempre simbolizzano veri e propri fonemi; anche poiché il numero di segni è normalmente minore del numero di fonemi utilizzati (in ogni caso di un qualche particolare linguaggio naturale)

in generale è vero che ogni linguaggio naturale è fondato su un particolare insieme di fonemi e su regole di trascrizione, nel contesto di un qualche suo peculiare insieme di segni (insiemi sempre stabilizzatisi posteriormente, rispetto al linguaggio vero e proprio (quello fonetico))

rispetto a ciò, l’eccezione sono i casi di trascrizioni sia pre alfabetiche che pre sillabiche
ad esempio, il caso dei geroglifici non sillabici (i geroglifici più antichi), oltre a tutti gli ulteriori casi fondati su ideogrammi – in tali casi i segni interfacciano direttamente la semantica (ciascun segno ↔ ciascun valore semantico (salvo sporadiche eccezioni)), così come anche avviene tra parole e semantica (parole = sotto insiemi di fonemi)

nel caso della Biblioteca immaginata da Borges, ovvia è la restrizione (rispetto all’universalità) dell’utilizzo di un qualche particolare insieme di segni (22 segni di un qualche particolare alfabeto così detto ‘latino’)

una soluzione veramente universale ["(passati presenti e futuri!!!)"] richiederebbe una codifica neutrale (dei segni ): ciascun linguaggio dovrebbe utilizzare una sua propria tabella di corrispondenza biunivoca, tra codifica universale e suoi propri segni (andrebbe bene qualsiasi possibile tabella di decodifica, poiché la Biblioteca di Borges è, in fin dei conti, veramente (ma veramente) molto stupida)

anche una soluzione fondata su un qualche set di caratteri latini può però venire comunque considerata sufficientemente universale

ad esempio, per un russo, seppure indubbiamente egli lo considererebbe disdicevole, non sarebbe granché difficile riprodurre una qualsiasi normale conversazione in russo mediante l’utilizzo di una sua trascrizione realizzata in caratteri latini

credo lo stesso dovrebbe valere anche per cinesi e arabi

a tal proposito, storicamente può venir citato il caso del turco: pur essendo un linguaggio tipicamente ari, in ragione della loro religione islamica per secoli si auto costrinsero nell’utilizzo di un set di caratteri semitici (ovviamente, corrispondendo ad altrettanto tipicamente semitici fonemi)

se è vero che per secoli e secoli per i turchi fu possibile utilizzare segni e fonemi tipicamente non ari, non vedo perché mai non dovrebbe anche valere l’opposto

(una eventuale contestazione me l’aspetterei (la auspicherei) in relazione all’attribuzione di tipologia ari ai così detti set di caratteri ‘latini’ (pare che i latini ari lo furono veramente (così come anche lo furono gli sciiti, gli unni, i turchi, i finnici, eccetera); a mio parere l’italiano, lo spagnolo, il portoghese ed il francese non furono però linguaggi tipicamente ari (e neppure dovrebbero risultare esserlo i corrispondenti set di caratteri))


circa il tempo immaginario eventualmente interverrò (per dire la mia) in una futura prossima occasione

Corrado-5834 ha scritto:

FranZeta ha scritto: Quello che sto per farvi notare infatti è un aspetto peculiare della Relatività Speciale che svanisce quando si generalizza la teoria a spazi curvi.

Interessante. Che altro potresti aggiungere a proposito?
Nella risposta tieni conto che io sono esperto di entrambe, mi interessa l'aspetto più propriamente matematico.
Secondo me Einstein si era accorto benissimo dei limiti e delle incongruenze della RS ed è per questo che ha sviluppato la RG.

Il perchè quello legato ai numeri immaginari sia un aspetto peculiare della Relatività Speciale è presto detto. Come già spiegato, la metrica euclidea è solo un caso particolare fra le infinite metriche che si possono postulare per uno spazio geometrico. Le metriche sono definite dal tensore metrico g_ij (siccome sei esperto del campo non sto a spiegare cosa siano questi oggetti di cui ora vado a parlare), e la distanza si scrive nella forma:

ds²=g_ijdxⁱdx^j

Normalmente i coefficienti indipendenti del tensore metrico (sono n*(n+1)/2, con n dimensione dello spazio geometrico) sono funzioni delle coordinate locali, tuttavia nel caso particolare della metrica euclidea questo tensore risulta essere il delta di Kronecker δ_ij, cioè una matrice identità, mentre nella metrica di Minkowski abbiamo una matrice "quasi identità":
e come già dicevo quel -1 è matematicamente equivalente all'aggiunta di un'unità immaginaria come coefficiente per la relativa coordinata locale, che nel nostro caso è la quarta, cioè operativamente ponendo:

dx⁴=icdt

Quindi possiamo salvare la metrica euclidea a patto di considerare il tempo una grandezza immaginaria. Ma se consideriamo tensori metrici g_ij generali, come avviene nella Relatività Generale, non c'è più alcun modo di "salvare" la metrica euclidea, anzi, tutta la teoria matematica utilizzata è proprio concepita come un superamento della geometria euclidea, perciò non c'è più nessuna convenienza nel considerare il tempo immaginario e si rischia piuttosto di fare confusione.

Qui bisognerebbe fare qualche annotazione: negli articoli originali Minkowski ed Einstein usano una metrica con i segni + e - scambiati rispetto a quanto ho fatto qui, la cosa però non ha importanza dato che quello che conta è il rapporto fra grandezze di tipo-spazio e tipo-tempo. Nondimeno nell'articolo di Minkowski è presente la seguente formula:

3*10⁵ Km = √-1 secs

che è per l'appunto una dichiarazione di equivalenza fra grandezze spaziali e grandezze temporali immaginarie.

Per quanto riguarda Einstein e la sua Relatività Generale, non è un mistero quale fosse il limite della Relatività Speciale che lo ha spinto ad elaborare la nuova teoria: non riusciva a incorporare una teoria della gravitazione. Come sappiamo per superare questo limite Einstein ha usato due ingredienti: il primo è la forma geometrica data da Minkowski alla R.S., il secondo è il Calcolo Assoluto elaborato da Ricci-Curbastro e Levi-Civita (sembrano quattro ma sono due), che a sua volta era il culmine di una serie di risultati matematici che partivano da Gauss e passavano da Riemann. Questo per quanto riguarda i limiti della R.S., sulle "incongruenze" non so invece a cosa ti riferisci. Come teoria matematica la R.S. è coerente, cioè non contiene contraddizioni, almeno non ne contiene di note. Ma se una contraddizione fosse infine trovata, questa spazzerebbe via anche la Relatività Generale assieme a quella speciale, dato che la prima è conseguenza logica della seconda. Siccome Einstein questo lo sapeva bene, avendola elaborata, escludo che volesse risolvere eventuali problemi della R.S. con una teoria da questa dipendente logicamente.

A livello matematico c'è anche un ulteriore ordine di idee che garantisce solidità alle due teorie. Lo delinea già chiaramente lo stesso Minkowski, facendo notare che il gruppo di Lorentz, che chiama G_c, è un oggetto più naturale del gruppo di Galileo G_∞, essendo quet'ultimo un caso limite del primo. Per fare un paragone sempre in ambito matematico, è un po' lo stesso rapporto che sussiste fra gli spazi di funzioni L^p e L^∞ (alla teoria dei quali, per pura combinazione, Minkowski ha pure dato un contributo). Minkowski nel suo articolo si spinge oltre, dicendo che sarebbe anche potuto accadere che qualche matematico dalle ampie vedute avesse potuto precognizzare la R.S. sulla base di queste considerazioni, e cioè che il gruppo G_c appare più naturale di G_∞, e solo l'altissimo valore di c avrebbe impedito fino ad allora di rendersene conto per via sperimentale. En passant, il gruppo G_c unifica i due tipi distinti di invarianza della Fisica Classica: l'invarianza per traslazioni e la prima legge di Newton.

La Relatività Generale estende ulteriormente questo ordine di idee, postulando l'invarianza delle leggi della fisica rispetto a diffeomorfismi (Principio di Covarianza Generale), e con ciò chiude il cerchio iniziato col Teorema di Noether. Questo stabilisce che l'invarianza rispetto ad un determinato gruppo di trasformazioni di un sistema fisico dia luogo ad integrali primi, cioè quantità conservate:

tempo ---> energia
traslazioni ----> quantità di moto
rotazioni ----> momento angolare

Per quanto riguarda le leggi della Fisica in generale, abbiamo questo climax:

Gruppo di Galileo ---> Meccanica Newtoniana
Gruppo di Lorentz ----> Relatività Speciale (ed Elettromagnetismo)
Covarianza Generale ---> Relatività Generale

Dunque a livello matematico non c'è nessuna contraddizione, ma anzi, un progressivo arricchimento della geometria dello spazio e del tempo verso principi di invarianza sempre più generali e naturali. Poi certamente sappiamo anche che R.G. e Meccanica Quantistica sono contraddittorie fra loro, ma questo è un discorso completamente diverso.

FranZeta ha scritto: non c'è più nessuna convenienza nel considerare il tempo immaginario e si rischia piuttosto di fare confusione.

In un certo senso questa è la risposta che speravo ...
Credimi se ti dico che i calcoli della RG me li sono rifatti tutti, anche usando una metrica pseudo-euclidea (a segnatura positiva) in un iperspazio 4-dimensionale, e non cambia nulla, almeno io non l'ho visto.

FranZeta ha scritto: Ma se una contraddizione fosse infine trovata, questa spazzerebbe via anche la Relatività Generale assieme a quella speciale, dato che la prima è conseguenza logica della seconda.

Non mi trovi d'accordo; anche se questo è quello che dicono tutti i libri.

FranZeta ha scritto: Poi certamente sappiamo anche che R.G. e Meccanica Quantistica sono contraddittorie fra loro, ma questo è un discorso completamente diverso.

E invece è proprio lo stesso discorso; l'origine della RS viene inteso da diversi autori in vari modi, compreso Einstein che cambiò idea numerose volte; chi dice che fu MMX, chi dice il problema della contrazione, etc... Una delle interpretazioni è che la teoria doveva risolvere l'incongruenza tra una parte della fisica, l'elettrodinamica, invariante secondo Lorentz ed un'altra, la meccanica, invariante secondo Galileo. Cento anni dopo siamo punto e a capo, una parte della fisica segue Lorentz, l'altra Galileo.

A proposito delle incongruenze della RS vorrei indirizzarti a questo lavoro, dove si sottolineano alcune sbavature, tipo usare assunzioni nascoste, che ad un matematico non dovrebbero lasciare indifferente:

www.neoclassicalrelativity.org/TheNinete...pecialRelativity.pdf

Corrado-5834 ha scritto:

FranZeta ha scritto: Ma se una contraddizione fosse infine trovata, questa spazzerebbe via anche la Relatività Generale assieme a quella speciale, dato che la prima è conseguenza logica della seconda.

Non mi trovi d'accordo; anche se questo è quello che dicono tutti i libri.

Mah, non è tanto il fatto che lo dicano tutti i libri, è che così come sono impostate le teorie è un dato di fatto. Siccome la R.S. è un caso particolare della R.G., e siccome una teoria matematica è vera soltanto se sono veri tutti i suoi casi particolari, la cosa è automatica. Per fare un esempio banale, la formula

1+2+...+n = n*(n+1)/2

è vera perchè vale per ogni numero naturale n, se ce ne fosse anche solo uno per cui non fosse valida la formula andrebbe rigettata tout court. Ma c'è anche un discorso più profondo da fare, perchè lo spazio-tempo di Minkowski non è un caso particolare come tanti altri: è un caso particolare di importanza capitale, dato che rappresenta lo spazio tangente alle varietà spazio-temporali curve di Einstein. Visto che tutto questo è in definitiva un argomento di geometria differenziale, per chiarirlo è conveniente fare l'analogia con le geometrie non euclidee. Anche qui abbiamo varietà curve, e lo spazio tangente a queste varietà è il comune piano (o iperpiano) euclideo, cioè Rⁿ. Se ci fosse qualcosa di contraddittorio in Rⁿ, questa contraddizione si trasferirebbe automaticamente anche a tutte le varietà curve, e in definitiva potremmo buttare tutta la geometria differenziale nell'indifferenziato.

Questo approccio, usato all'inverso però, servì ad Eugenio Beltrami per dimostrare la consistenza relativa delle geometrie non euclidee: costruendo un modello di geometria iperbolica nello spazio euclideo dimostrò che se la geometria euclidea è consistente lo è anche la geometria non euclidea, e viceversa. Dato che il rapporto tra spazio-tempo di Minkowski e varietà di Einstein è lo stesso, la coerenza della R.G. dipende indissolubilmente da quella della R.S.

Poi certamente sappiamo anche che R.G. e Meccanica Quantistica sono contraddittorie fra loro, ma questo è un discorso completamente diverso.

A proposito delle incongruenze della RS vorrei indirizzarti a questo lavoro, dove si sottolineano alcune sbavature, tipo usare assunzioni nascoste, che ad un matematico non dovrebbero lasciare indifferente:

www.neoclassicalrelativity.org/TheNinete...pecialRelativity.pdf

La cosa ti stupirà ma queste "sbavature" in realtà mi lasciano del tutto indifferente. Innanzitutto perchè per quanto mi riguarda l'impostazione definitiva della R.S. è quella di Minkowski del 1907, e non di Einstein del 1905, perciò tendo a ignorare le critiche all'articolo di Einstein. Una volta che la R.S. diventa geometria, e con Minkowski lo diventa, a livello matematico quello di cui bisogna preoccuparsi sono i postulati della geometria. Anche i postulati di tipo fisico, cioè quelli riguardanti la bontà del modello rispetto all'universo in cui viviamo, mi interessano relativamente poco, e comunque sono un discorso diverso dalla coerenza matematica.

Ma veniamo alle "sbavature". Non mi pare che la Fisica Classica si sia mai preoccupata delle sbavature delle geometria euclidea, sebbene questa fosse il quadro di riferimento di tutta la disciplina. Eppure queste sbavature c'erano, erano evidenti da secoli e sono state sistemate solo nel 1899 da Hilbert col suo Grundlagen der Geometrie, che per inciso avrà letto solo una piccola percentuale di fisici. Per coincidenza, anche gli assiomi di Hilbert sono 19, se escludiamo quello delle parallele.

I vettori della Fisica, altro esempio, sono diversi da quelli della matematica: c'è una diffusa ed endemica tendenza ad ignorare il concetto di "fibrato tangente" fra fisici e ingegneri, eppure anche in questo caso non ravviso particolari preoccupazioni dovute a questo tipo di "sbavature". Insomma il rigore matematico è universalmente considerato eccessivo per altre discipline scientifiche, e con buone ragioni, direi. Ma, ripeto, la R.S. (secondo Minkowski) è una teoria di Fisica Matematica, cioè è matematica a tutti gli effetti, e lo standard di rigore con cui è sviluppata è quello proprio delle teorie matematiche, ecco perchè mi sento abbastanza sicuro nel dichiarare che non sia contraddittoria.

Per concludere il mio modestissimo parere sull'inconciliabilità di R.G. e M.Q. è questo: la prima è una teoria classica, cioè basata sul concetto di continuum spazio-temporale, la seconda invece si basa (in linea generale, ci sono poi moltissime diverse interpretazioni) su uno spazio-tempo discreto. Tutto qui. Credo anche che abbia ragione la M.Q. per quanto riguarda la vera natura dello spazio-tempo, e che la R.G. sia un'ottima approssimazione valida per tutti quei casi in cui le dimensioni del sistema fisico permettono di ignorare la quantizzazione.

FranZeta ha scritto: Ma, ripeto, la R.S. (secondo Minkowski) è una teoria di Fisica Matematica, cioè è matematica a tutti gli effetti, e lo standard di rigore con cui è sviluppata è quello proprio delle teorie matematiche, ecco perchè mi sento abbastanza sicuro nel dichiarare che non sia contraddittoria.

Ma il problema non è la coerenza interna della teoria ma la sua aderenza ai fatti sperimentali. E qui fisici e matematici differiscono enormemente; il matematico si preoccupa solo della coerenza formale, il fisico vuole far quadrare i fatti sperimentali.
Tu dici che ti interessa solo Minkosky, al fisico non può bastare; la critica al lavoro originale di Einstein è precisa e puntuale ed il pasticcio che fece è ben evidente; la qual cosa può avere conseguenze importantissime, non basta fare una teoria matematicamente coerente.
Tanto per fare un esempio, le equazioni dell'elettrodinamica non coincidono con le equazioni di Maxwell. Lo sapevi che esistono formulazioni alternative (Weber, Hertz, ...) che differiscono nel formalismo e non sono perfettamente sovrapponibili dal punto di vista logico?
Lo sai che c'è uno che ha fatto una elettrodinamica covariante secondo Galileo?

www.omicsonline.org/open-access/back-to-...000198.php?aid=80761

Permettimi infine una nota ironica a latere,
Ma lo sai che la Flat Earth Society usa la RS per spiegare il suo modello?

theflatearthsociety.org/tiki/tiki-index....e=Special+Relativity

FranZeta ha scritto: Relatività Speciale ==> Tempo Immaginario?

dove i è l’unità immaginaria, cioè la radice quadrata di -1 (ne ho già parlato su questo forum qui e qui ).

Ciò che FranZeta dice, normalmente mi convince
talvolta anche mi affascina: in matematica, al suo confronto, io certamente sono un ignorante

rimpiango di non aver dedicato alla matematica una maggior parte del mio tempo (specialmente in gioventù); peraltro, anche so che oramai è troppo tardi: oramai sono troppo vecchio; dentro di me le energie, di anno in anno divengono sempre più insufficienti; mentre, per contro, la preservazione della mia salute sempre più richiede la mia facoltà di centellinarle (purtroppo)

su una questione matematica fondamentale il mio pensiero è però totalmente divergente, rispetto al pensiero di FranZeta

la questione è quella dei così detti ‘numeri immaginari’
(a mio parere, è questione di superstizione (superstizione degli antichi e dei moderni – detta alla Moses Finley))

di seguito espongo brevemente le mie principali ragioni

magari fui eccessivamente presuntuoso (quien sabe?)

il fatto è che leggendo The Road to Reality, di Roger Penrose, mi venne il sospetto che circa il campo complesso egli non avesse idee affatto chiare

pertanto ripresi in mano un vecchio testo universitario, che avevo conservato, proponendomi di rinfrescare le mie proprie nozioni, nel merito delle funzioni continue elementari

quando affrontai la questione dell’esponenziale complesso cominciarono a torcermisi le budella (diventò infine odio allo stato puro: un odio viscerale)

di seguito mi dissi: se non ti piace, prova a reinventarla

dunque, pertanto poi quella parte della matematica la reinventai

la fondai sulle spirali esponenziali, assumendo che il campo complesso altro non è che l’insieme di tutte le spirali esponenziali

per i calcoli utilizzai openoffice.calc;
per visualizzare quanto i calcoli producevano utilizzai DraftSight (2D e 3D)

nella costruzione delle spirali esponenziali trovai la possibilità di utilizzare un numero infinito di differenti algoritmi

anche però scovai tutte le ragioni di ciascun possibile algoritmo,
ed anche trovando tutte le necessarie regole di conversione
(ed anche tante altre cosine, tutte a mio parere molto interessanti)

ebbene, ancora oggi sono straconvinto del fatto che la teoria che costruii è molto più generale (e molto meno superstiziosa) di quella standard (quella a tutt’oggi prevalentemente utilizzata)

dico ‘standard’ (ed anche parlo di “teoria prevalentemente utilizzata”) al solo fine di cautelarmi – contro la mia possibile ignoranza di produzioni realizzate da a me sconosciuti autori, che possano aver precedentemente già costruito e già proposto teorie alternative, rispetto a quella standard

ammetto che la mia ignoranza è immensa

ebbene, di seguito due differenti risultati numerici prodotti da tre algoritmi tra loro differenti (nella teoria che escogitai sono tutti e tre algoritmi legittimi, ed anche producendo risultati sempre perfettamente consistenti)

i tre differenti algoritmi ed i due differenti risultati del caso i^i :

1) exp_C(z, w) ↦ z^w = (ρ, θ)∈ℂ
… (ρ_z, θ_z)∈ℂ
… (ρ_w, θ_w)∈ℂ
… ρ = ρ_z^(ρ_w×cos(θ_w));
… θ = θ_z×ρ_w×cos(θ_w);

… i^i = (1, 0)

2) exp_C(z, w) ↦ z^w = (ρ, θ)∈ℂ
… (ρ_z, θ_z)∈ℂ
… (ρ_w, θ_w)∈ℂ
… ρ = ℯ^(−θ_z×ρ_w×sin(θ_w));
… θ = ln(ρ_z)×ρ_w×sin(θ_w);

… i^i = (0.207879576…, 0)

3) exp_C(z, w) ↦ z^w = (ρ, θ)∈ℂ
… (ρ_z, θ_z)∈ℂ
… (ρ_w, θ_w)∈ℂ
… ρ = ρ_z^(ρ_w×cos(θ_w)) × ℯ^(−θ_z×ρ_w×sin(θ_w));
… θ = θ_z×ρ_w×cos(θ_w) + ln(ρ_z)×ρ_w×sin(θ_w);

… i^i = (0.207879576…, 0)

un penultimo fatto è che, tra tutti gli algoritmi capaci di produrre spirali esponenziali, (e per varie ragioni) il più primitivo pare proprio dover essere il n° 1 (tutti gli altri sarebbero da esso derivabili)


una nota conclusiva:

a fronte di superstizioni io proprio non posso starmene in silenzio

a mio parere, il parlare di FranZeta di numeri ‘immaginari’ e di tempo ‘immaginario’ è una delle conseguenze che le superstizioni producono

prevedo una sua notevole irritazione (e ciò mi dispiace ...)

gino sighicelli ha scritto: quando affrontai la questione dell’esponenziale complesso cominciarono a torcermisi le budella (diventò infine odio allo stato puro: un odio viscerale)

Hahahaha, non sai quanto ti capisco !!!

Bella questa idea delle spirali esponenziali ...

Ma sui numeri complessi stai esagerando, in realtà sono altrettanto reali dei numeri Reali.
Se ti limiti ad usarli come uno strumento e nient'altro, passa la paura.
Il problema semmai è quello di non complicare le cose semplici.

Mi pare tu sia un informatico, no?
E allora non puoi non conoscere i Quaternioni, altro che numeri immaginari!
E l'uso che se ne fa nella Game Industry.
Ma pure quella è solo una moda, si potrebbe risolvere lo stesso problema con gli angoli di Eulero, o anche con semplici matrici.

E' che ogni tanto ci piace, e i matematici ne soffrono come gli altri, inseguire qualcosa che fa figo!
E la fisica pure c'ha i suoi bei problemi in questo senso.

@Corrado
Forse non mi sono spiegato bene quando dicevo che la bontà di un modello di fisica matematica non mi interessa in quanto matematico. La questione la vedo in realtà così: mentre gran parte dei fisici sono alla ricerca DELLA teoria, la giusta, vera e definitiva Teoria del Tutto, penso che la maggior parte dei matematici abbia un atteggiamento più prudente, e consideri i vari modelli della fisica matematica per quello che sono: modelli. Poi saranno gli esperimenti a dare un giudizio sulla loro aderenza al mondo reale, ma penso che in pochi si illudano che un giorno si possa arrivare al "modello definitivo". Nondimeno la storia insegna che la matematica pura ha un legame assai profondo con il mondo fisico, ma è proprio la profondità del legame e la vastità delle possibilità matematiche a dare un freno alle aspettative di umana comprensione della questione.

Tornando alla Relatività, lo so che esistono molte proposte alternative, resta il fatto che per come è impostata la coerenza della R.G. è dipendente da quella della R.S., se si vuole renderla indipendente bisogna modificarla in qualche suo aspetto e poi riscriverla da capo con una nuova matematica, perchè la matematica dei tensori è proprio quella che sancisce questa dipendenza logica.

@Gino
Avevo rimosso, ma ora che me lo fai notare ricordo di averti già risposto in merito a questa tua teoria alternativa dei numeri complessi. Che ti devo dire? Il campo dei numeri complessi è uno solo, indipendentemente da come lo si definisca, quindi finchè i tuoi algoritmi forniscono il risultato corretto, nel nostro caso iⁱ=e^-π/2+2kπ, sono un'alternativa accettabile, quando non lo fanno sono sbagliati. Tertium non datur. Tra parentesi c'è un'inutile complicazione nel tuo modo di impostare il calcolo, perchè non c'è bisogno di ricorrere a una funzione di due variabili complesse quando si può usare la comoda funzione z^z. Nel campo reale si può usare per dare un senso all'espressione indeterminata 0⁰(=1!).

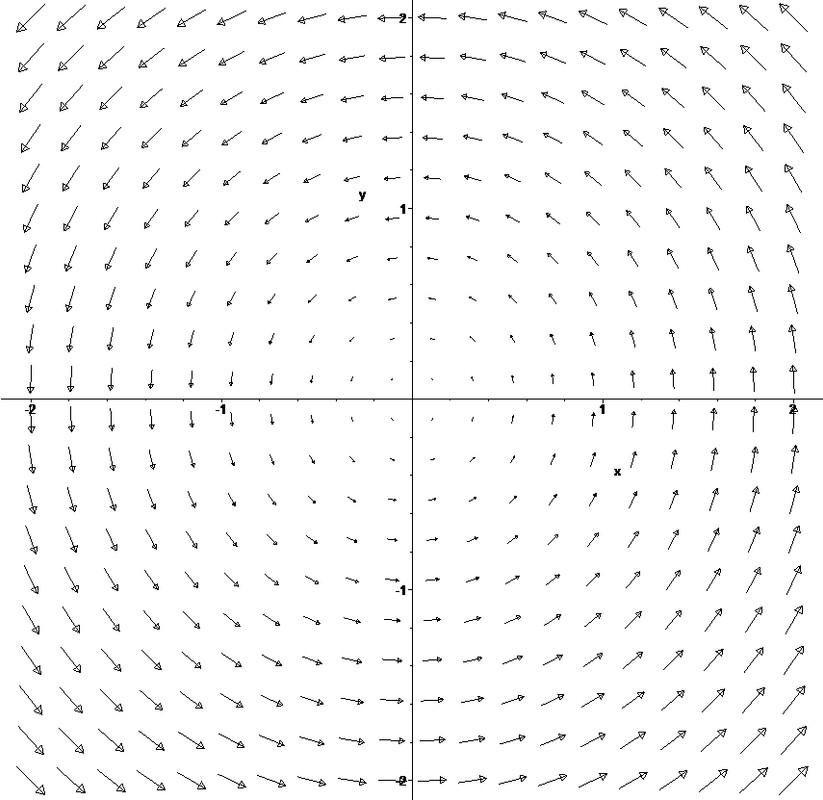
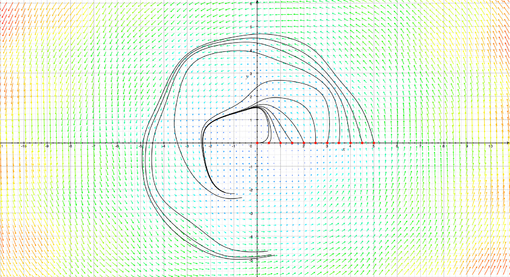
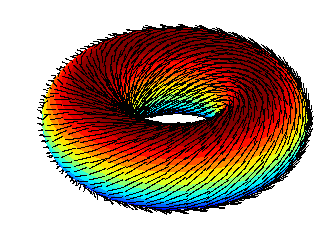
Devi anche considerare che i numeri complessi non sono per niente un oggetto misterioso, fin dal XIX secolo per esempio lo studio di una funzione non può prescindere dal suo comportamento nel campo dei numeri complessi. Per non parlare dell'algebra, dove sono di casa da quasi mezzo millennio. Anche l'esponenziale complessa, che ti ha fatto di male? Ha la stessa identica definizione della funzione reale, ma molte belle e comode proprietà in più. Io la uso per ricordarmi le formule di cos(nx) e sin(nx), giusto per dirne una. Si può anche visualizzare senza problemi nella forma di campo vettoriale (i vettori sono riscalati per starci nel riquadro):

Aggiungo qualche considerazione all'ultimo commento, relativamente alla risposta che avevo dato a @Gino. Innanzitutto il termine "numeri immaginari" è puramente convenzionale, può ancora oggi apparire evocativo, ma semanticamente non ha nulla a che fare con l'immaginazione (lasciamo stare la superstizione poi...) così come il termine tecnico "numeri reali" non ha a che fare con la realtà o "numeri razionali" con la razionalità, e così via.

Dal punto di vista storico questi numeri acquistano un primo timido diritto di cittadinanza matematica quando gli algebristi italiani del XVI secolo si trovano davanti a equazioni come questa:

x³-15x-4=0

Si vede facilmente che una soluzione è x₁=4, dividendo il polinomio di terzo grado per (x-4) e applicando la formula risolutiva per equazioni di secondo grado si trovano anche le altre due soluzioni:

x₂=-2+√3

x₃=-2-√3

Tuttavia i suddetti algebristi italiani avevano anche trovato la formula risolutiva per equazioni di terzo grado, e applicandola all'equazione originale ottenevano:

x=(2+√-121)^1/3+(2-√-121)^1/3

ossia:

x=(2+11√-1)^1/3+(2-11√-1)^1/3

Dato che l'equazione aveva le tre radici reali x₁,x₂,x₃ già calcolate per altra via, iniziarono a pensare che quella radice di meno 1 non fosse poi così priva di senso, dato che poteva produrre risultati reali. Tutto questo accadeva 500 anni fa, poi arrivò Eulero che usò la notazione √-1=i e scoprì le sue meravigliose formule, Gauss che ci insegnò a vedere i numeri complessi come punti del piano, e poi tanti altri che contribuirono a costruire l'attuale teoria. Una teoria ricca di risultati profondi e inaspettati.

Per quanto riguarda la funzione esponenziale complessa, come già detto ha la stessa definizione della funzione reale, quindi non c'è nessun motivo di distinguerle anche a livello di notazione. La funzione di due variabili complessi che nel suo commento sopra @Gino chiama exp_C(z,w) in realtà si denoterebbe z^w (le notazioni in matematica sono fondamentali, perchè se ognuno usa le sue non si capisce più una mazza...) e risultano le seguenti uguaglianze:

z^w = e^{w log z} = e^{w (log|z|+iArg z)}

dove |z| e Arg z sono rispettivamente il modulo e l'argomento del numero complesso z. Normalmente si pone z=x+iy, ma lo stesso numero complesso si può anche scrivere in forma polare come

z=|z| e^{i Arg z}

Quest'ultima è la forma usata sopra da Gino, con ρ_z=|z| e θ_z=Arg z. Se poniamo θ_z=f(ρ_z), con f funzione continua monotona qualunque, otteniamo delle spirali nel piano complesso, non so se queste siano le famose spirali di cui parla Gino. In ogni caso, esprimendo entrambi i numeri complessi in forma polare, la formula giusta per la funzione z^w è la terza:

ρ = ρ_z^{ρ_wcos(θ_w)} e^{−ρ_wθ_zsin(θ_w)}

θ = ρ_w(θ_zcos(θ_w) + log(ρ_z)sin(θ_w))

Va da sè che le prime due sono incomplete, e quindi sbagliate. In ogni caso, scritta così, la funzione z^w non è solo molto più brutta, ma a livello concettuale ci troviamo di fronte allo stesso problema che avevamo all'inizio. Prendiamo infatti l'espressione ρ_z^ρ_w che compare all'inizio della prima formula, notazione a parte questa è proprio la funzione originale z^w ristretta al caso in cui z e w sono variabili reali positive, cioè in pratica è la funzione di due variabili reali positive x^y. Ora, come si fa a calcolare questa funzione? Si fa così:

x^y = e^{y log x}

...che è esattamente quello che avevamo fatto sopra con la funzione originale z^w. Ma allora non valeva la pena di tenerci l'originale?

Come ogni tanto capita uso questo spazio per commentare/rispondere a questioni nate altrove. Stavolta relativamente a questo commento di @kamiokande. Devo precisare per chi non andasse a vedersi il commento originale che nel testo citato qui sotto non si sta rivolgendo a me, ma all'utente @Cum grano salis. Io invece mi rivolgo direttamente a kamiokande.

Quella discussa è manco a farlo apposta la stessa equazione che sostenevi non fosse Lorentz-invariante perchè "se kA=kB non significa che A=B", discussione nella prima pagina di questo thread. Comunque:

Ovviamente da te nessun commento sulla legge

Che è ovviamente sbagliata, perché se si muove un pezzo di circuito immerso in un campo magnetico costante nasce ovviamente una forza elettromotrice e quindi una corrente (come l'esperimento di Faraday insegna), ma la formula sopra non prevede alcuna forza (o campo elettrico) nel circuito. Quindi si scrive

Quando uno usa tre volte in due righe l'avverbio "ovviamente" mi aspetterei di leggere una cosa veramente ovvia, e invece...e invece, in realtà, la prima equazione prevede correttamente che non ci siano correnti indotte in un circuito in quiete rispetto al campo costante (nel tempo) B, mentre è proprio e solo la seconda a prevedere l'assenza di correnti nel circuito in moto che stiamo testando, sbagliando clamorosamente. I dettagli del perchè le cose stanno così li lascio a chi sta studiando l'argomento per l'esame di elettromagnetismo, o è fresco di studi, come dilettevole (e semplice) esercizio.

Non solo: se scritta nelle coordinate solidali al circuito, la prima equazione diventa esattamente come a suo tempo l'avevo scritta qua , riquadro 7, cioè la versione accentata dell'equazione originale, e siccome in queste nuove coordinate B non è più costante, l'equazione prevede -ancora correttamente- che si generi nel circuito una corrente indotta. Chissà, forse è per questo motivo che tutti i testi di elettrodinamica riportano la prima equazione e non la tua: perchè questa funziona.

Ci sarebbe anche quest'altra cosa:

Io personalmente propendo per la seconda che è più diretta, e prevede solo l'uso dei campi classici B ed E invece che B ed E' (che non è un campo ma la cosiddetta forza elettromotrice introdotta da Maxwell nel 1895, e la cui paternità si attribuisce erroneamente a Lorentz), anche se è equivalente alla prima (in realtà non è proprio così, ci sono delle differenze, ma non ho ne tempo ne voglia di spiegarti il perché).

Vorrei capire come accidenti fa E' a non essere un campo vettoriale, se è definito come somma di due campi vettoriali. Sarebbe come dire che 10 metri più 5 metri fa 15 chili. In effetti E’ rappresenta la “forza di Lorentz per unità di carica” (cfr. la citazione qui sotto), ed è un campo vettoriale più che legittimo. Mi sorge il sospetto che tu non abbia ben chiaro cosa sia un campo vettoriale, in queste circostanze diventa difficile non dico contestarne la validità, ma anche solo capire a cosa si riferiscano le equazioni di Maxwell.

Tra parentesi la questione che hai provato a sollevare non è certo un arcano segreto per fisici dissidenti, ad esempio Feynman nelle sue Lectures on Physics la tratta così:

…la "regola del flusso" - cioè che la forza elettromotrice in un circuito è uguale alla variazione del flusso magnetico all'interno del circuito - si applica sia che il flusso cambi perchè cambia il campo sia perchè si muove il circuito (o entrambe le cose).
...
Eppure nella nostra spiegazione della regola abbiamo usato due leggi completamente distinte per i due casi - v x B per circuiti in movimento e rot E per cambiamenti del campo.

Non conosciamo altre aree della fisica dove un tale semplice, accurato e generale principio necessiti per la sua comprensione di un'analisi in termini di due differenti fenomeni. In genere simili meravigliose generalizzazioni si deducono da un singolo profondo principio sottostante. Invece, in questo caso, non sembra esserci nessuna profonda implicazione del genere. Dobbiamo trattare la "regola" come l'effetto combinato di due fenomeni piuttosto distinti.

Possiamo guardare alla "regola del flusso" nel seguente modo. In generale, la forza per unità di carica è F/q = E + v x B. Nei fili in movimento c'è la forza derivante dal secondo termine. Inoltre, esiste un campo E se da qualche parte c’è un campo magnetico che cambia. Sono effetti indipendenti, ma la forza elettromotrice lungo un circuito è sempre uguale alla variazione del flusso magnetico attraverso esso.

Che bel vespaio ha tirato su Kamiokande ahahahahaha

Franzeta ti dico subito che l'equazione che ho scritto non ha nulla a che vedere con le equazioni di Maxwell-Lorentz della discussione che abbiamo avuto tempo fa. Prima di entrare nella questione, visto che hai ritirato fuori la discussione che abbiamo avuto sull'invarianza, ti vorrei brevemente ricordare che la questione non era, e non è, "se kA=kB non significa che A=B", ma questa:



a cui la tua risposta è stata questa



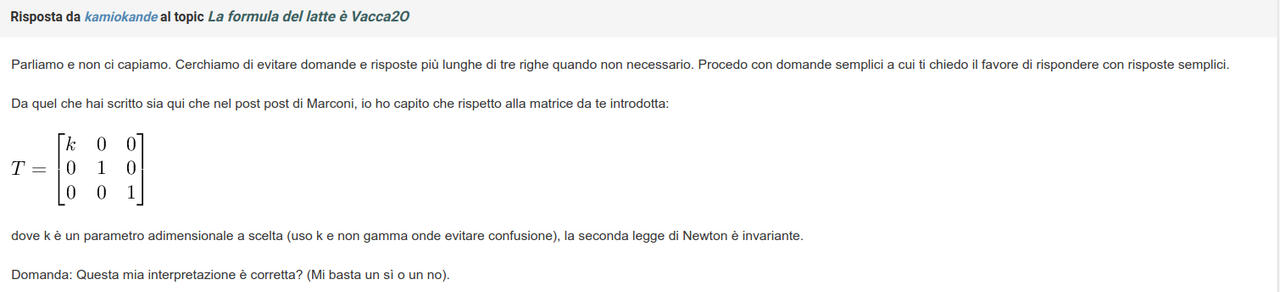
Visto che tu sei ancora convinto che le cose stiano così, ed io sono ancora convinto del contrario, mi faresti la cortesia di trovare un libro di fisica (titolo, autore, edizione e pagina) dove si affermi che la seconda legge di Newton è invariante rispetto (oltre che a rotazioni, traslazioni, traslazioni temporali e trasformazioni inerziali) anche ad una trasformazione T come quella da te definita? Trovane anche solo uno che tu ritieni darti ragione, io me lo studio e se ti dà davvero ragione non ho nessun problema a darti ragione; dopodiché potremo, qualora lo vorrai, continuare il discorso sulla legge di Faraday.

kamiokande ha scritto: Franzeta ti dico subito che l'equazione che ho scritto non ha nulla a che vedere con le equazioni di Maxwell-Lorentz della discussione che abbiamo avuto tempo fa.

Mah, vedi un po' tu, è la stessa equazione scritta nella stessa notazione, se ritieni che non abbiano nulla a che vedere ogni ulteriore discussione è priva di senso.

Visto che tu sei ancora convinto che le cose stiano così, ed io sono ancora convinto del contrario, mi faresti la cortesia di trovare un libro di fisica (titolo, autore, edizione e pagina) dove si affermi che la seconda legge di Newton è invariante rispetto (oltre che a rotazioni, traslazioni, traslazioni temporali e trasformazioni inerziali) anche ad una trasformazione T come quella da te definita? Trovane anche solo uno che tu ritieni darti ragione, io me lo studio e se ti dà davvero ragione non ho nessun problema a darti ragione; dopodiché potremo, qualora lo vorrai, continuare il discorso sulla legge di Faraday.

Guarda, il problema era di una semplicità disarmante, se ancora oggi non l'hai capito non so che farci. I riferimenti che cerchi non sono nei libri di fisica, ma in quelli di algebra lineare, dato che la matrice T si riferisce a un isomorfismo fra spazi vettoriali e non, come sei tutt'ora convinto, a una trasformazione del sistema di coordinate xⁱ. Tecnicamente T (per essere precisi T^-t, la trasposta dell'inversa) trasforma la base dello spazio tangente dove vivono i vettori considerati, in quel caso "F" e "m*a", e ci dice che se due vettori sono uguali in una base continuano ad essere uguali anche nell'altra base. Ma questo è un modo di incasinare un discorso semplicissimo, dato che la trasformazione agisce solo su una componente, quindi in definitiva se la guardi come relazione fra scalari non è altro che la regola di semplificazione "kA=kB --> A=B" che vale in ambiti generalissimi: basta che k sia invertibile e che valga la proprietà associativa.

Guarda, il problema era di una semplicità disarmante, se ancora oggi non l'hai capito non so che farci. I riferimenti che cerchi non sono nei libri di fisica, ma in quelli di algebra lineare, dato che la matrice T si riferisce a un isomorfismo fra spazi vettoriali e non, come sei tutt'ora convinto, a una trasformazione del sistema di coordinate xⁱ. Tecnicamente T (per essere precisi T^-t, la trasposta dell'inversa) trasforma la base dello spazio tangente dove vivono i vettori considerati, in quel caso "F" e "m*a", e ci dice che se due vettori sono uguali in una base continuano ad essere uguali anche nell'altra base. Ma questo è un modo di incasinare un discorso semplicissimo, dato che la trasformazione agisce solo su una componente, quindi in definitiva se la guardi come relazione fra scalari non è altro che la regola di semplificazione "kA=kB --> A=B" che vale in ambiti generalissimi: basta che k sia invertibile e che valga la proprietà associativa.

Grazie per la risposta, ma la tua opinione la conosco già, ti ho chiesto gentilmente di fornirmi un libro di fisica o al più una dispensa di corso universitario nel quale si specifichi chiaramente che, oltre alle trasformazioni che ho elencato, anche la trasformazione da te indicata lascia invariata la seconda equazione di Newton. Visto che la cosa è di una semplicità disarmante, non ti sarà difficile il compito e basterà una ricerca di qualche minuto per portarlo a termine. Aspetto con ansia.

A questo punto mi riesce difficile credere che tu dica sul serio, e inizia a venirmi il sospetto che la tua intenzione sia piuttosto quella di prendermi per il culo. In entrambi i casi non ho certo intenzione di riprendere da capo la discussione della prima pagina. Tuttavia, volendo dare una possibilità al caso che davvero tu dica sul serio, aggiungo qualche riga, definitiva, su un argomento che non meritava certo l'attenzione che gli abbiamo dato in questo thread.

Visto che insisti coi riferimenti bibliografici io ho studiato su questo:

Appunti di Geometria 1, P. Ellia, Pitagora Editrice Bologna

dove si tratta la teoria degli spazi vettoriali e in particolare i cambiamenti di base. Non è casuale che per chi studia fisica, matematica o ingegneria questo esame si faccia al primo anno ed elettromagnetismo al secondo: senza la teoria degli spazi vettoriali e delle funzioni lineari è un po' difficile affrontare quella degli operatori differenziali agenti su campi vettoriali. Posso anche fornire un suggerimento metodologico per capire i termini della questione. Si consideri il campo di forza:

F(x,y,z)=r/|r|³

con r=(x,y,z). Si può pensare, a meno di costanti, come un campo elettrostatico, o anche gravitazionale, se proprio gli si vuole dare consistenza fisica. Si applichi ora la trasformazione rappresentata dalla matrice T alle coordinate, ricavando r'=T*r e facendo l'opportuna sostituzione si ricavi F(x',y',z'). Tenendo poi conto che F=(F₁,F₂,F₃), si applichi ora la stessa matrice T alle componenti di F, ossia si calcoli T*F, e si confronti questa espressione con quella ottenuta in precedenza.

F(x',y',z') è il tipo di trasformazione che si trova nei libri di fisica, perchè è (anche) di interesse fisico stabilire se F sia o meno invariante rispetto a un determinato gruppo di trasformazioni delle coordinate. T*F invece si trova nei libri di algebra lineare, perchè questo tipo di invarianza vale qualunque sia il campo vettoriale F, nel senso che se vale l'equazione vettoriale F=G, con F e G campi vettoriali, allora vale sempre anche l'equazione T*F=T*G, e viceversa, perciò T non è di nessuna utilità nel determinare le caratteristiche dei campi vettoriali considerati. E' però utile quando si tratta di fare calcoli con vettori e campi vettoriali, e il fatto che non sia nei libri di fisica non significa che non sia accettata dai fisici, ma solo che viene data per acquisita (dai libri di algebra lineare). Va da sè che se poniamo G=m*a abbiamo proprio la seconda legge di Newton come caso particolare.

Detto questo, ti ricordo che questa cosa che dura da un anno e mezzo è nata da una tua supercazzola volta a negare l'evidenza, e l'evidenza era: γ*(quantità = 0 per ipotesi) = 0, si veda sempre il calcolo già linkato, sempre riquadro 7, in corrispondenza dei tre asterischi. Se in un anno e mezzo non siamo riusciti nemmeno a concludere che gamma per zero fa zero, prima di arrivare a parlare *davvero* di equazioni di Maxwell la vita su questo pianeta potrebbe essere già estinta. Ovviamente negherai, come già al tempo, che la questione sia un γ*0=0, ma da allora non hai aggiunto nulla di diverso dalla suddetta supercazzola. Per concludere: questo tuo incaponirti nel chiedermi riferimenti bibliografici su un'argomento che cerchi nel posto sbagliato (libri di fisica invece che di algebra lineare), oltre ad avere un chè di donchisciottesco, non va a cozzare solo contro i mulini a vento, ma anche col fatto che tendi ad ignorare ogni riferimento bibliografico che in qualche modo si scontra con le tue convinzioni, e.g. Lorentz-invarianza delle equazioni di Maxwell.

Caro FranZeta a questo punto non se io devo pender seriamente queste tue affermazioni, perché "you had only one job"! Ovvero trovare un libro di fisica che ti desse ragione sull'invarianza della legge di Newton, ma ovviamente ritorni con un libro di Geometria nel quale per l'appunto non c'è quello che ti ho chiesto, perché in Geometria i cambiamenti di base possono essere qualunque, in fisica no. Ora siccome mi dici che tu hai studiato su quel libro senza portarmi ad esempio un solo libro di fisica, mi fa venire il dubbio che tu la fisica non l'abbia studiata, e visto le cose che scrivi il dubbio è quasi una certezza. Ho insistito sul riferimento bibliografico perché il riferimento bibliografico che ti dà ragione NON ESISTE! Infatti in FISICA per trasformazioni che lasciano invariate le leggi della meccanica, e quindi anche F=m*a, si intendono SOLO ED ESCLUSIVAMENTE le trasformazioni che lasciano invariata l'accelerazione a.

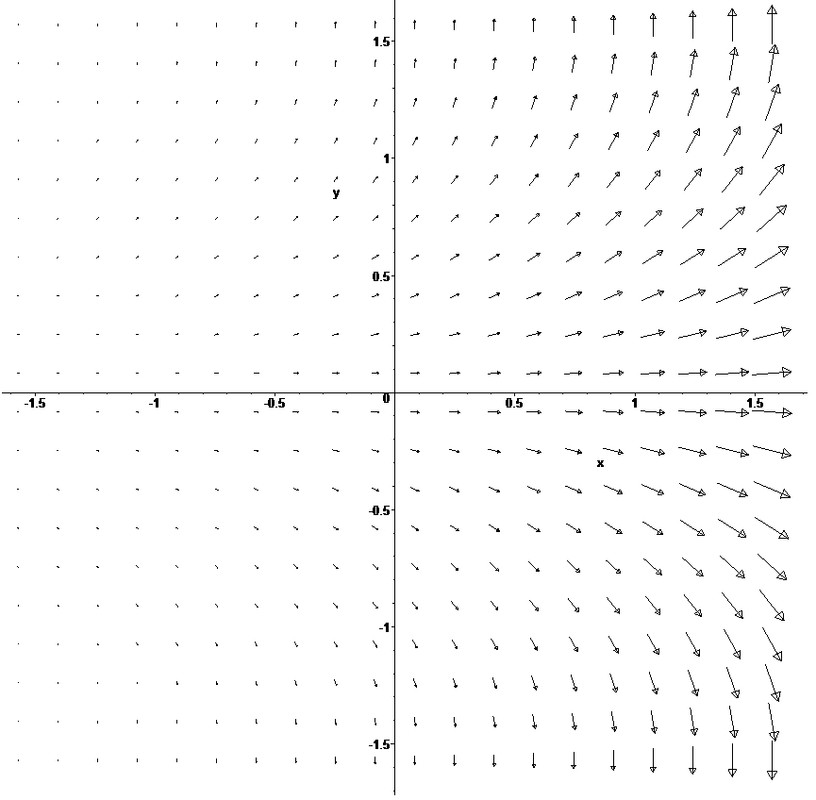
Sperando che "repetita iuvant", ti rifaccio di nuovo un esempio numerico come feci già a suo tempo. Definendo un vettore posizione r = ( 0.5*t² , t² , 1.5*t² ) e derivandolo due volte nel tempo si ottiene il vettore accelerazione a = ( 1 , 2 , 3 ) . Derivando due volte il vettore posizione trasformato r' = T*r = ( 0.5*k*t² , t² , 1.5*t² ) si ottiene il vettore accelerazione trasformato a' = ( k , 2 , 3 ). Essendo la matrice T costante si può anche trasformare direttamente a in a' senza passare per la derivata. Ora, credo che sia piuttosto evidente a tutti che a = ( 1, 2, 3 ) è diverso a' = ( k , 2 , 3 ) sia in modulo che in direzione, infatti



per quel che riguarda il modulo, e



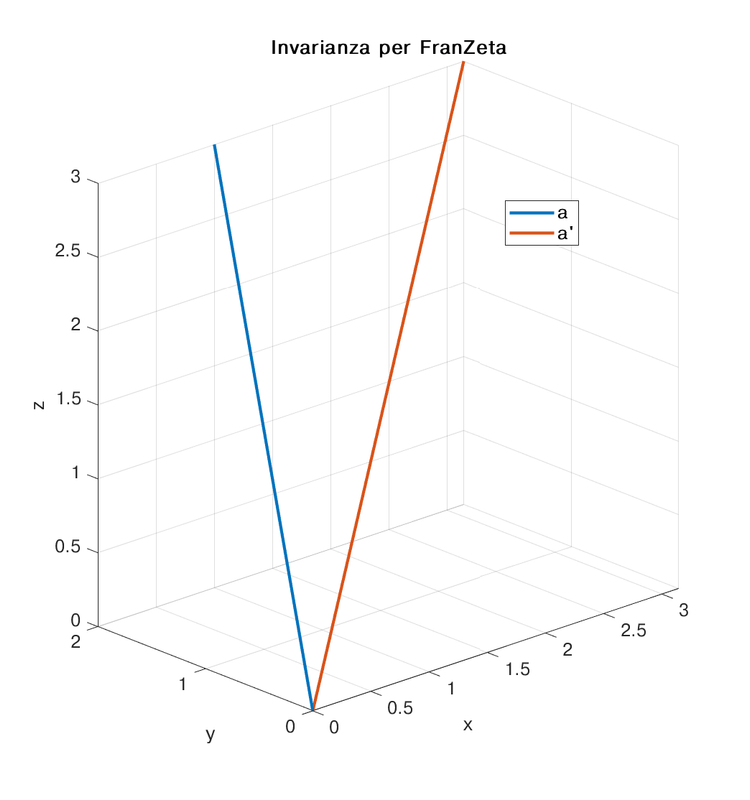
per quel che riguarda i coseni direttori. A chiunque conosca un minimo di fisica è quindi più che evidente che la trasformazione T NON LASCIA INVARIATA la seconda legge di Newton. Per renderlo più chiaro ti faccio un disegnino, posto k = pi greco la tua invarianza si manifesta così.



È francamente imbarazzante che tu, FranZeta, che ti ritieni esperto di fisica e che pretendi di insegnarla agli altri, non riesci a capire questo semplice concetto di fisica che di norma si insegna alle superiori.

Potrei anche chiudere qui, ma siccome ti ostini nel tuo atteggiamento alla marchese Del Grillo ("io sono io e voi non siete un cazzo") scrivendo oltretutto una sequela di sciocchezze clamorose, tipo che io avrei detto che "se kA = kB non è detto che A = B", cosa che non solo è falsa, perché non l'ho mai sostenuto, ma sottintende neanche troppo velatamente che io sia un cretino (e come se io scrivessi "FranZeta sostiene che se A = B e B = 0, A può essere diverso da 0", non sto scrivendo apertis verbis che sei cretino, ma è ovvio che io lo sottintenda).

Ma andiamo un po' di più nel dettaglio della questione, in quello che si chiama gruppo delle cosiddette trasformazioni galileiane che lasciano invariate le leggi della meccanica classica, e quindi anche F=m*a, sono presenti SOLO ED ESCLUSIVAMENTE: traslazioni spaziali, traslazioni temporali, rotazioni spaziali e trasformazioni inerziali (o di Galileo). I due soli casi particolari che lasciano invariate le leggi della meccanica classica senza far parte del gruppo di Galileo sono: le riflessioni che trasformano discretamente le terne destrorse in sinistrorse (e viceversa), e la variazione di scala isotropa (dove k è applicato a tutte le componenti) che, come già evidenziato da Newton, rappresenta un cambiamento di unità di misura (passando per esempio da metri e secondi a cubiti e clessidre, le leggi della fisica non possono variare appunto perché k*F=k*m*a). Per di più, il gruppo di Galileo è formato da trasformazioni affini la cui matrice associata è SOLO ED ESCLUSIVAMENTE ortogonale (perché devono necessariamente lasciare invariate le distanze), con il determinate che può solo essere +1. A te sarà più che ovvio che la matrice T ha determinate pari a k e quindi NON PUÒ FAR PARTE DEL GRUPPO DI GALILEO, e quindi NON PUÒ LASCIARE INVARIATE LE LEGGI DELLA MECCANICA.

Andando un po' oltre alla mera questione matematica si può osservare che l'invarianza alle traslazioni implica l'omogeneità dello spazio e del tempo, mentre l'invarianza alle rotazioni implica l'isotropia dello spazio. Si può vedere immediatamente che la trasformazione T implicherebbe la non isotropia dello spazio, in quanto se si pongono tre aste lunghe un metro rispettivamente lungo gli assi X, Y e Z, nel sistema trasformato l'asta in direzione X verrebbe ad essere lunga k metri (o 1 cubito, o qualunque unità di misura ti venga in mente scegliendo opportunamente k), mentre lungo Y e Z le aste continuerebbero ad essere lunghe un metro, non lasciando inalterate le distanze.

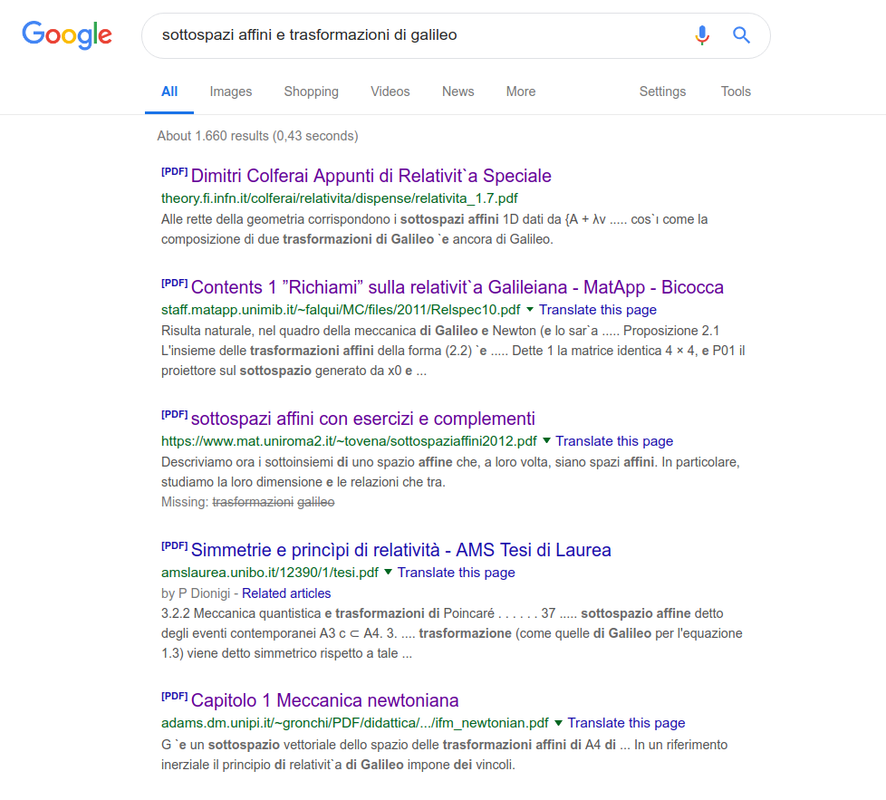
Se avessi speso 2 minuti 2 a cercare per esempio su Google "sottospazi affini e trasformazioni di galileo" avresti trovato diverse dispense di fisica che dicono sostanzialmente la stessa cosa, ovvero che io ho ragione e tu torto.



Prediamo per esempio Il quinto link nella lista, ovvero gli appunti di fisica matematica di Giovanni Federico Gronchi, che tra le altre cose insegna Istituzioni di Fisica Matematica all'università di Pisa

adams.dm.unipi.it/~gronchi/PDF/didattica...12/ifm_newtonian.pdf

che in due paginette due, la 15 e la 16, dice esattamente quel che dico io. Se non ti basta questo ti posto anche due paginette del libro "Essential Dynamics & Relativity", prima edizione, di Peter J. O'Donnel, docente e ricercatore del Dipartimento di Matematica Applicata e Fisica Teorica a Cambridge

Pagina 15

Pagina 16

Caso vuole che alle stesse pagine dica le stesse cose. Come vedi siamo proprio all'inizio del libro, quindi parliamo dei concetti di base. Ma se ancora non ti bastasse ho anche altri libri ed articoli scientifici che ribadiscono esattamente gli stessi concetti.

Conclusione, la matrice T NON LASCIA INVARIATA la legge F=m*a, di conseguenza la tua definizione di invarianza in fisica NON ESISTE, non basta che la matrice sia invertibile o che componente per componente si mantenga la stessa equazione per avere lo stesso comportamento fisico, perché, se così non fosse caro FranZeta, avresti trovato la trasformazione che lascia invariato tutto: le leggi della meccanica, le equazioni di Maxwell, l'equazione di Schrödinger e così via. Dovresti renderti conto da solo di quanto questa cosa sia inverosimile, ma ovviamente così non è.

Parliamo adesso della equazione di Faraday che ho scritto nel post sui buchi neri (anche se in realtà era sulla Blavatsky)

Mah, vedi un po' tu, è la stessa equazione scritta nella stessa notazione, se ritieni che non abbiano nulla a che vedere ogni ulteriore discussione è priva di senso.

In effetti non ci sarebbe neanche da discutere sulla questione, perché a chi conosce la fisica e le equazioni di Maxwell dovrebbe essere già abbastanza chiaro che sono due cose diverse. Ma siccome tu sei un po' (tanto) confuso sulla questione, ti do una rinfrescata. La velocità che appare nelle equazioni di Maxwell trasformate (secondo Einstein) non ha nulla a che vedere con la velocità nella cosiddetta forza di Lorentz. Infatti nella forza di Lorentz la velocità che compare è la velocità relativa tra il campo magnetico e la carica o il conduttore, che qui chiamo u e che può anche non essere costante. Nelle equazioni di Maxwell trasformate, invece, la velocità v (rigorosamente costante) è quella di un qualunque sistema di riferimento in moto uniforme rispetto al sistema considerato in quiete, sistema in quiete nel quale si scrivono le classiche equazioni di Maxwell. Per definizione la velocità del sistema di riferimento in moto può essere qualunque, purché sia costante, e non ha nulla a che vedere con il moto delle cariche o dei conduttori. Infatti, se confiniamo nello spazio un campo elettrico E ed un campo magnetico B fermi rispetto ad un sistema di riferimento considerato in quiete, in un sistema in moto uniforme rispetto al primo non ci saranno più i campi E e B ma compariranno i campi E' e B' secondo le note trasformazioni. Il tutto avviene in totale assenza di cariche e conduttori, perché secondo Einstein questo è un puro e semplice effetto cinematico (per Lorentz non è così visto che il fenomeno è dovuto al moto del sistema di cariche, o ioni come li chiamava lui in principio, nell'etere che è considerato in quiete assoluta). A scanso di equivoci, questo è quello che scrive Einstein nel paper del 1905:

[...]

Now to the origin of one of the two systems (k) let a constant velocity v be imparted in the direction of the increasing x of the other stationary system (K), and let this velocity be communicated to the axes of the coordinates, the relevant measuring-rod, and the clocks.

[...]

Now the principle of relativity requires that if the Maxwell-Hertz equations for empty space hold good in system K, they also hold good in system k; that is to say that the vectors of the electric and the magnetic force—(X' , Y' , Z' ) and (L' , M' , N' )—of the moving system k [...]


Detto questo, se rimuoviamo il campo elettrico ed introduciamo una carica o un conduttore a riposo rispetto al campo magnetico, ovviamente non nasce alcuna forza, e siccome anche rispetto al sistema in moto non c'è nessun moto relativo tra la carica o il conduttore ed il campo B', non nascerà allo stesso modo alcuna forza (qui dovremmo aprire una lunga parentesi, ma lasciamo perdere). Se come dici tu una forza nasce, addio al principio di relatività, perché rispetto a due sistemi inerziali avremmo due comportamenti fisici diversi (per esempio una carica che sta ferma per il sistema in quiete, ma che si muove con velocità non costante per il sistema in moto uniforme).

Piccola nota l'equazione da me scritta è ovviamente (e banalmente) sbagliata. Ho inserito un errore più che evidente nella speranza che la persona a cui era indirizzato il post se ne accorgesse, così da dargli almeno il beneficio del dubbio sulla sua effettiva competenza. Ma a quanto pare non solo non se n'è accorto lui, ma non te ne sei accorto nemmeno tu "che sai e che hai studiato". Infatti così come è scritta, se il campo B è costante nel tempo il rotore di E' (che qui sarebbe il campo ausiliario E' = E + u x B, e non il campo trasformato E' a causa di v) è uguale a zero. Infatti potrei scrivere anche



con F e P campi vettoriali qualunque, ma se



per come è scritta la formula abbiamo

.

Invece tu, caro FranZeta, stai sostenendo che

Quando uno usa tre volte in due righe l'avverbio "ovviamente" mi aspetterei di leggere una cosa veramente ovvia, e invece...e invece, in realtà, la prima equazione prevede correttamente che non ci siano correnti indotte in un circuito in quiete rispetto al campo costante (nel tempo) B, mentre è proprio e solo la seconda a prevedere l'assenza di correnti nel circuito in moto che stiamo testando, sbagliando clamorosamente. I dettagli del perchè le cose stanno così li lascio a chi sta studiando l'argomento per l'esame di elettromagnetismo, o è fresco di studi, come dilettevole (e semplice) esercizio.

Ovvero

"Se A = B, il fatto che B = 0 non implica che A = 0".

Perché nell'equazione rot E' = -dB/dt nascerebbe comunque una forza nonostante B sia costante nel tempo. Ora tu questa cosa l'hai scritta nero su bianco, al contrario della frase, o del concetto, che tu hai attribuito erroneamente a me. Ma l'apice ineguagliabile è questo:

Non solo: se scritta nelle coordinate solidali al circuito, la prima equazione diventa esattamente come a suo tempo l'avevo scritta qua , riquadro 7, cioè la versione accentata dell'equazione originale, e siccome in queste nuove coordinate B non è più costante, l'equazione prevede -ancora correttamente- che si generi nel circuito una corrente indotta. Chissà, forse è per questo motivo che tutti i testi di elettrodinamica riportano la prima equazione e non la tua: perchè questa funziona.

Il grassetto l'ho aggiunto io. Visto che tu sei un matematico, mi spieghi come da una combinazione lineare di grandezze fisiche costanti nel tempo (gamma, v, E, B) possa nascere una grandezza fisica variabile nel tempo? Ricapitolando, tu scrivi che "Se A = B, il fatto che B = 0 non implica che A = 0", e che se in qualche modo si fanno apparire i campi accentati (inserendo un sistema di riferimento qualunque purché in moto uniforme) compaiono magicamente anche forze elettromotrici che nell'altro sistema non ci sono (mandando in vacca il principio di relatività, tanto per intenderci), e poi sono io quello che scrive sciocchezze.

Ritornando alla fisica, la formula corretta è quindi questa



Che è stata ricavata nel 1890 (ovvero due anni prima che Lorentz introducesse esplicitamente la forza elettromagnetica, equazione 61 pag. 443 , forza che era stata esplicitata per primo da Maxwell nel 1865, equazione D pag 485 ) da uno de passaggio, un certo Heinrich Hertz che, oltre a dimostrare sperimentalmente l'esistenza delle onde elettromagnetiche, ha condensato, insieme (in senso figurato) ad Heaviside, le equazioni di Maxwell nella forma che oggi viene riportata nei libri di elettrodinamica (sia Lorentz che Einstein hanno basato le loro teorie elettromagnetiche sui lavori di Hertz e di Heaviside). Una cosa che Hertz ha fatto, e che non tutti sanno, è stata estendere le equazioni di Maxwell, valide solo per i corpi a riposo, anche ai corpi in movimento, equazione 1a pag. 245. Hertz , infatti, ricava quella equazione per un corpo deformabile in moto (con velocità u) immerso in un campo elettrico e magnetico (lavoro citato anche da Lorentz). Ora se si considera che div B = 0 si ottiene la formula



Che solo nel caso in cui la velocità u non vari nello spazio (moto rigido), si può scrivere nella forma (grazie ad una nota identità vettoriale che non riporto per brevità)



e quindi ecco spiegato perché ho scritto nell'altro thread che le due formule non sono propriamente equivalenti. La formula così scritta in entrambi i modi prevede giustamente (come ho già scritto nell'altro thread) che se vario la forma di un circuito immerso in un campo magnetico costante (che è uno degli esperimenti di Faraday, nel quale viene mossa solo una parte del conduttore), nel circuito si forma una corrente. Dovrebbe esserti ormai palese che la formula scritta nei libri di elettrodinamica non prevede invece alcuna forza. Quindi come ho detto e riconfermo le equazioni da me scritte non centrano nulla con le equazioni trasformate di Maxwell-Lorentz-Einstein da te ricavate quel dì di tenebra.

Ritorno infine anche su un'altra affermazione che feci riguardo le equazioni di Maxwell, ricordando che il problema sollevato da Oleg D. Jefimenko (un altro poveraccio de passaggio che ha solo risolto le equazioni de Maxwell, "ma che vole signora mia! Oggi so tutti raccomandati"), e non da kamiokande di LuogoComune, ovvero che se in ambo i membri delle cosiddette equazioni di Faraday ed Ampere rimane un fattore gamma nella sola componente X, la forma vettoriale delle equazioni di Maxwell NON è invariante rispetto alle trasformazioni di Lorentz. La cosa di per se sarebbe piuttosto ovvia, visto che se il fattore gamma non c'è nelle equazioni di partenza non può esserci nelle equazioni di arrivo, quindi o il fattore è in tutte le componenti di ambo i membri (invarianza di scala) o altrimenti, come in questo caso, non si può semplificare e lì rimane. Tu FranZeta hai sostenuto che la presenza del parametro gamma non causa alcuna modifica della fisica dei fenomeni. Anche questa affermazione è decisamente imbarazzante, quanto o forse anche di più di quella sull'invarianza (ma ne è figlia perché nella tua mente non può essere che così).

Come ti ho già fatto notare a suo tempo, ma tu ovviamente non hai capito, svolgendo un semplice esperimento mentale (che qui ti semplifico ulteriormente) si può dimostrare la non invarianza della legge di Faraday, invalidando la tua tesi. Prendiamo un circuito chiuso formato da un semplice conduttore a riposo in un campo magnetico variabile nel tempo, ma fisso nello spazio. Rispetto al sistema di riferimento solidale con il conduttore (e con il campo), si genera una corrente nel conduttore per via della legge di Faraday. Inoltre, essendo la velocità del sistema di riferimento v = 0 il fattore gamma di Lorentz è uguale ad 1, e quindi (con o senza gamma nelle componenti X) anche l'equazione trasformata si riduce banalmente alle solita legge di Faraday. Introduciamo ora un sistema di riferimento in moto rispetto al primo con velocità v > 0, e quindi gamma > 0. Rispetto a questo sistema l'equazione va trasformata secondo Einstein, ma se rimane il fattore gamma di Lorentz nella componente X del rotore di E' e nella componente X del campo magnetico B', si deve prendere atto che sia la forza elettromotrice nel circuito (rot E') che il campo magnetico (B') dipenderanno in modo diretto dal fattore gamma. Quindi pur valendo ancora la legge di Faraday, abbiamo che la forza elettromotrice, ovvero la corrente nel circuito, per il sistema in moto sarà funzione della velocità del sistema di riferimento (!!) a causa del fattore gamma nella componente X. È possibile scegliere così una qualunque velocità del sistema di riferimento (!!) tale da incrementare la corrente fino a far fondere il circuito a causa dell'effetto Joule, arrivando al paradosso che per il sistema in quiete l'esperimento funziona normalmente, ma per il sistema in moto il circuito si rompe. Conclusione, il principio di relatività viene invalidato e giocoforza non c'è alcuna invarianza delle leggi della fisica.

Facendo 2 + 2 con i miei post precedenti, ora capisci che in tutta la discussione avuta tra te e me hai sempre avuto torto? E che quindi, se le sole componenti lungo X da ambo i membri delle cosiddette leggi di Faraday e Ampere sono moltiplicate per gamma, le equazioni di Maxwell in forma vettoriale NON SONO INVARIANTI rispetto alle trasformazioni di Lorentz? Io francamente ne dubito, ma spero che chi avrà la voglia di leggere capisca questa cosa.

FranZeta ti do io ora un consiglio: continua a parlare di matematica quanto ti va, ma evita per cortesia di parlare di fisica (almeno fino a quando l'avrai studiata un po'), perché se vuoi ci sarebbero da analizzare un altro paio di tue affermazioni in merito a questioni di fisica (e parliamo di primo principio della termodinamica) da far accapponare la pelle.

@kamiokande
Qua di imbarazzante c'è solo la tua preparazione posticcia ed evidentemente da autodidatta che vuoi spacciare per conoscenza della materia, e addirittura fare le pulci a gente come Feynman, giusto perchè sopra l'ho citato, che hanno studiato l'equazione della legge di Farady e non hanno trovato nessun "ovviamente è sbagliata". Non hai ancora capito la differenza fra coordinate e componenti, cioè non sei in grado di vedere la differenza fra F(T*r) e T*F(r), con l'ultimo spunto credevo che almeno avessi provato a fare il conto per vedere cosa succedeva, invece niente, continui imperterrito con le tue supercazzole. Ti lascio da solo in questa tua riscrittura della fisica e, a quanto pare, anche dell'algebra lineare. Quando pubblicherai la tua teoria completa fammi un cenno che due risate me le faccio volentieri.

EDIT Viste e considerate le cazzate del tuo ultimo commento, facciamo una prova pratica: puoi gentilmente calcolare esplicitamente l'espressione di F(x',y',z') ottenuta per cambio sistema di coordinate come suggerivo sopra?

kamiokande ha scritto: FranZeta ti do io ora un consiglio: continua a parlare di matematica quanto ti va, ma evita per cortesia di parlare di fisica (almeno fino a quando l'avrai studiata un po'), perché se vuoi ci sarebbero da analizzare un altro paio di tue affermazioni in merito a questioni di fisica (e parliamo di primo principio della termodinamica) da far accapponare la pelle.

Visto che non ti vuoi sporcare le mani con un semplice calcolo fatto di tuo pugno (dubito che si trovi lo stesso conto nella pur vasta bibliografia che consulti), chiudo da parte mia la faccenda, non prima di averti ricordato che l'invarianza di un'equazione rispetto a un gruppo di trasformazioni è matematica, dunque a rigore quello che starebbe sconfinando materia saresti tu, ma dato che non sei nemmeno un fisico la questione si fa più complicata.

Riassumo e tiro le conclusioni, esprimendomi solo sul tuo ultimo commento, perchè la vita è breve e non si può perdere tempo su ogni singola cazzata che ti presenta.

1) All'inizio di tutta la discussione c'è un calcolo esplicito della Lorentz-invarianza dell'equazione considerata. In quel calcolo non risulta nessun fattore gamma nella prima componente dei campi vettoriali. Quindi, non avendo ricevuto nessuna segnalazione di errori nel calcolo, e hai avuto quasi due anni per cercarli, continuo a ritenere valida questa espressione (peraltro universalmente adottata nella letteratura sull'argomento) e non quella col fattore gamma. Se davvero tieni alla tua teoria alternativa dell'elettromangetismo dovrai prima o poi fare i conti con questo aspetto, perchè se quel calcolo è giusto tutti i tuoi discorsi crollano miseramente senza ulteriori discussioni.

2) Ma volendo per puro esercizio intellettuale ipotizzare che quel fattore gamma ci sia davvero, questo provocherebbe in qualche modo le correnti indotte della tua [strike]masturbazione[/strike] sperimentazione mentale? Ma neanche per idea, per calcolare la circuitazione di E' bisogna integrare rot E' e non "rot E' con la prima componente moltiplicata per gamma", quindi in qualche modo il fattore gamma va fatto sparire prima di integrare. Come si fa? Si semplifica con l'altro gamma a secondo membro, e il risultato è nessuna corrente indotta aggiuntiva. La cosa è perfettamente coerente col teorema di algebra lineare che ci dice che se abbiamo due vettori F, G e un'applicazione lineare invertibile T, allora T*F=T*G se e solo se F=G. Nella tua nuova fisica invece questo teorema non vale, e di conseguenza anche tutto il resto dell'algebra lineare, che andrà riscritta in forma coerente e "kamiokande-invariante".

3) Dubito assai che il povero Jefimenko, da te tirato per la giacchetta in un discorso che difficilmente condividerebbe nella sua rozza inaccuratezza, abbia mai voluto portare avanti questo tipo di argomentazioni. Ritengo più probabile che sia piuttosto tu a non avere capito una mazza dei suoi scritti e ad aver riportato esattamente quello che hai capito. Questa ipotesi è supportata da una curiosa coincidenza: se scriviamo i campi E' e B' rispetto a una base solidale col vecchio riferimento, ecco che in effetti compare un fattore gamma nella prima componente. In pratica si cambia sì il sistema di coordinate, ma si tiene la vecchia base ∂/∂xⁱ dello spazio tangente. D'altronde Jefimenko faceva qualcosa di analogo anche con l'altra equazione, quella della legge di Gauss. Avrà avuto le sue buone ragioni per scrivere le equazioni in questo riferimento ibrido -un po' nuove e un po' vecchie coordinate - ma sono quasi certo che queste ragioni non siano quelle che gli vuoi attribuire te.

Epilogo

A questo punto che tu non sia per nulla un fisico è acclarato, perchè un fisico non metterebbe mai insieme tante sciocchezze inerenti la propria materia. Qualunque cosa tu sia, trovo stupefacente come si possa ritenere che le migliori menti del XX secolo siano passate su questi concetti senza accorgersi di simili banali incongruenze. Ma te li vedi Majorana e Heisenberg che discutono del loro principio di indeterminazione e non si sono nemmeno accorti di problemi tanto stupidi relativi alle trasformazioni di Lorentz? O un Poincaré, che scopre tra le altre cose il caos deterministico e la relatività ristretta prima di Einstein, senza mai accorgersi che l'equazione della legge di Faraday è "ovviamente sbagliata"? In pratica pensi che tutta questa gente qua era una manica di fessi (Jefimenko escluso, ma solo perchè non l'hai capito, se no era fesso pure lui), ma per fortuna oggi abbiamo un kamiokande che ci svela tutte le banalità che questi personaggi non sono riusciti a vedere. Ora fai pure la tua replica, posta i tuoi link inutili quando non proprio avulsi dal discorso, poi però chiudiamola qui perchè con uno che ragiona come te non c'è nessuna possibile soddisfazione intellettuale, ma solo una gran rottura di coglioni.

Avrei voluto leggere le tue risposte ma ho dovuto fermarmi subito a questa tua affermazione:

Qua di imbarazzante c'è solo la tua preparazione posticcia ed evidentemente da autodidatta

Io non ho tempo da perdere dietro a soggetti come te, quindi questo sarà probabilmente il mio ultimo commento sulla questione. Ti faccio notare che, ad oggi, non hai portato nemmeno un libro di fisica a dimostrazione delle cose che scrivi, al contrario del sottoscritto. Il gioco è semplice: si fa una affermazione e si porta a dimostrazione un libro od una dispensa di corsi universitari di fisica. Vediamo se con un ulteriore esempio riesci a capire la cosa.

Affermazione. Le leggi della meccanica classica rimangono invariate solo ed esclusivamente da: traslazioni, rotazioni e trasformazioni inerziali o di Galileo. Tempo due minuti su Google per cercare "galiean invariance" e si trova questo documento

lss.fnal.gov/archive/other/inp-1556-ph.pdf



A pagina 5 si può leggere



Quindi, come è ben noto, le trasformazioni di Galileo hanno la forma dell'equazione 2.1 dove: il vettore a rappresenta la traslazione dell'origine (traslazioni spaziali rigide), b le traslazioni temporali, il vettore u è la velocità del secondo sistema di riferimento in moto rispetto al primo (trasformazioni inerziali u*t) , e la matrice R è una matrice ortogonale che rappresenta la rotazione del sistema di riferimento (trasformazioni ortogonali). Ma continuando, a fine di pagine 7 ed inizio di pagina 8, c'è scritto



La forza F si trasforma sempre (always) con F' = R*F (equazione 2.10), dove R è la matrice rigorosamente ortogonale definita all'equazione 2.1 (di cui sopra), altrimenti la forza non avrebbe la stessa intensità in tutti i riferimenti inerziali. Ma andiamo avanti, a fine pagina 15 ed inizio pagina 16 c'è scritto



Per avere una forma Galileiana covariante delle leggi della meccanica una forza deve trasformarsi rigorosamente con l'equazione 2.10 (sempre di cui sopra), e quindi con trasformazioni rigorosamente ortogonali aggiungo io. Il caso classico una forza costante F0, esattamente come quella dell'esempio che ti ho fatto al post #28271 , si può trasformare solo ed esclusivamente come F0' = R*F0, con R matrice ortogonale. Se così non è, l'intensità (modulo) del vettore forza cambia da sistema a sistema, così come cambia l'intensità del vettore accelerazione (per via della legge di Newton).

Proseguiamo ora con lo stesso concetto espresso in modo più fisico e meno matematico.

Da "Essential Dynamics and Relativity" Peter J. O’Donnell, CRC Press 1st Edition , sempre al post #28271 , pagina 12 capitolo 1.1.3



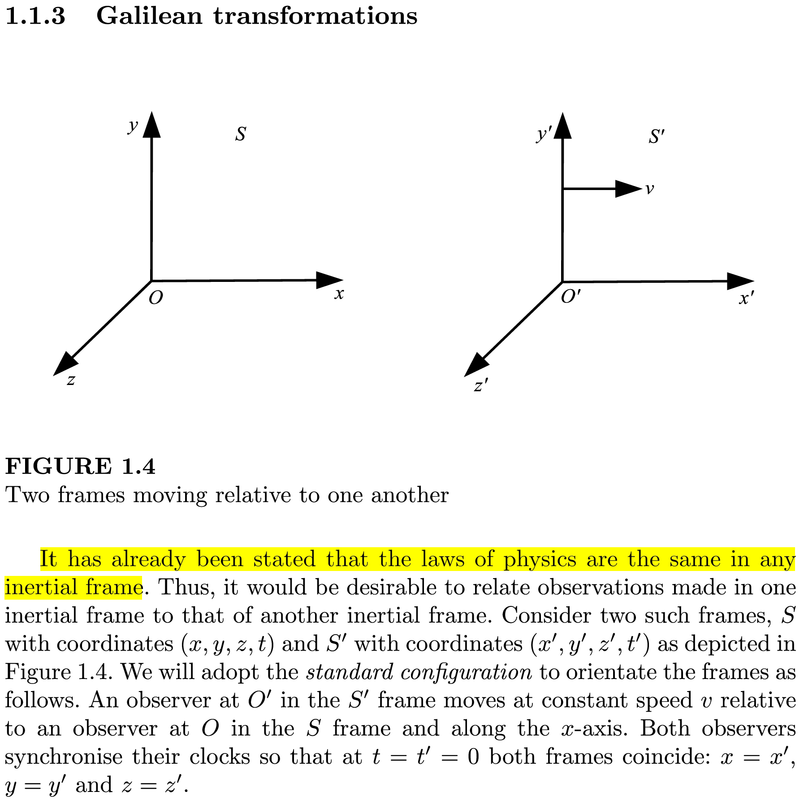
Come già detto (sia qui nel forum che nel libro, n.d.K) le leggi della fisica sono le stesse in qualunque riferimento inerziale. Si definiscono quindi sue sistemi di riferimento: S con coordinate (x,y,z,t) ed S' con coordinate (x',y',z',t'), con S' in moto rispetto ad S con un velocità costante v. A fine pagina 13 ed inizio pagina 14, ci viene detto che



Le trasformazioni inerziali (galilean boost) tra i due sistemi di riferimento S ed S' (definiti a pagina 12 di cui sopra): non lasciano invariato il vettore posizione r, non lasciano invariato il vettore velocità u, ma lasciano invariato il vettore accelerazione a. Perciò (therefore), entrambi i sistemi inerziali misurano la medesima accelerazione dell'oggetto in studio (in questo caso una torcia elettrica introdotta a pagina 12). Il capitolo 1.1.3 si apre dicendo che le leggi della fisica sono le stesse in qualunque sistema di riferimento inerziale, e si chiude dicendo che nonostante r e u non siano invarianti alle trasformazioni inerziali, la condizione necessaria e sufficiente (per i sistemi di particelle n.d.K) affinché le leggi della fisica siano le stesse è che a sia invariante (rimanga la stessa) in tutti i sistemi di riferimento inerziali.

Prima conclusione: non essendo la tua matrice T ortogonale non può far parte delle trasformazioni di Galileo e quindi non può lasciare invariata la legge F = m*a (generale covarianza). Ovvero, essendo a' = T*a diverso da a, e ti sfido a dimostrare il contrario, la trasformazione T non lascia invariata la seconda legge di Newton. La trasformazione associata alla matrice T non può quindi riferirsi ad un sistema di riferimento inerziale. Ti è chiaro quindi che fino ad ora mi sono solo limitato a leggerti testi di fisica?Ne dubito.

Affermazione: Le trasformazioni generalizzate di Galileo rappresentano l'omogeneità dello spazio e del tempo e l'isotropia dello spazio. Sempre da "Essential Dynamics and Relativity" Peter J. O’Donnell, CRC Press 1st Edition, pagina 15 e 16



Direi che è più che sufficiente, la forma generale è la stessa dell'articolo "On the Galilean covariance of classical mechanics" così come in qualunque testo di fisica, punto. la matrice R deve essere ortogonale altrimenti lo spazio perde la proprietà dell'isotropia come dall'esempio al post #28271 . Di nuovo, non sto interpretando nulla, ti sto leggendo testi di fisica. Questo scambio lo possiamo intitolare: "Kamiokande legge libri di fisica a FranZeta, ma FranZeta non capisce". Fino a qui abbiamo parlato di acqua calda, ovvero di invarianza o generale covarianza, che non sono propriamente la stessa cosa, ma siccome tu non capisci il concetto di base è inutile provare a fare un ragionamento di dettaglio.

Seconda ed ultima conclusione: se la tua matrice T non lascia invariata a seconda legge di Newton, il tuo concetto di invarianza componente per componente è sbagliato, quindi le leggi di Faraday e di Ampere in forma vettoriale NON sono invarianti rispetto alle trasformazioni di Lorentz, come per altro trovato da Jefimenko e non dal sottoscritto, che stai cercando di convincere con supercazzole.

Qui trovi tutte le pagine dalla 12 alla 16 così magari impari qualcosa, ma ne dubito.

Fine parte 1 di 2.

Parte 2 di 2.

Ora parliamo di moti relativi, quindi sempre di acqua calda.

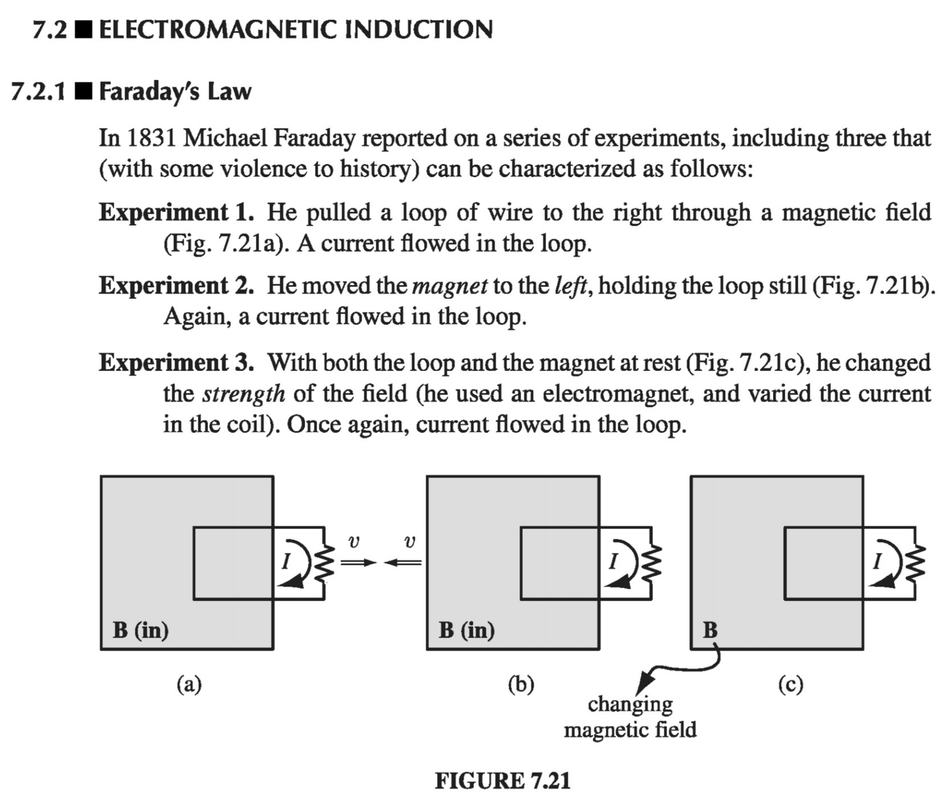
Affermazione. La velocità presente nella forza di Lorentz non ha nulla a che vedere con la velocità nei campi trasformati secondo Einstein. Parto da un disegnino preso da pagina 312 del libro "Introduction to electrodynamics" di David J. Griffiths , Pearson, Fourth edition.



A questa figura manca un esperimento fondamentale, quello in cui parte del circuito è in quiete rispetto al campo B e parte viene mosso facendo variare la forma del conduttore, che altrimenti rimane rigido. A parte questo punto, che sarebbe di fondamentale importanza per una discussione seria, ma che è sprecato in questa farsa a cui mi sto prestando, si vede bene che la velocità v è la velocità relativa tra campo e conduttore nel sistema di riferimento del laboratorio (che è uno solo). Infatti subito dopo a pagina 313 dice



Quindi non ci deve sorprendere il fatto che l'esperimento (a) e l'esperimento (b) della figura 7.21 diano lo stesso risultato perché è solo la velocità relativa tra campo e conduttore ad importare. Infatti nella teoria della relatività deve essere così. Ora andiamo ad un altro libro, "The Classical Theory of Fields" di Landau e Lifshitz, io ho la quarta edizione, ma ho scoperto che su internet si trova la terza versione in pdf e che andrà bene uguale

www.elegio.it/mc2/LandauLifshitz_TheClas...oryOfFields_text.pdf

A pagina 48 viene definita la forza di Lorentz



v è definita come la velocità (relativa) della carica che si muove nel campo magnetico H. Siccome la carica è soggetta in generale ad un campo elettrico E ed un campo magnetico H, la formula ci dice che la carica è soggetta ad una forza, ovvero che il moto non sarà uniforme e quindi v non sarà in generale costante (a figura 6 di pagina 57 questa cosa si vede bene, ma spero che almeno questo ti sia ovvio).

Tra pagina 62 e 63 vengono discussi i campi trasformati secondo Einstein



in queste formule la velocità non è v, ma V che appunto si riferisce alla velocità relativa tra due sistemi di riferimento qualunque K e K'. Ora per fugare ogni dubbio andiamo a pagina 9



K e K' sono due sistemi di riferimento inerziali qualunque con velocità relativa V che è, per la definizione di sistema di riferimento inerziale, costante.

Il vettore v rappresenta perciò il moto di una carica in un campo elettrico e magnetico, e quindi v è generalmente diverso da una costante. Per un conduttore, invece, è chi esegue l'esperimento che decide il valore di v, e siccome non c'è nessun motivo fisico perché sia mantenuto sempre costante, in generale è diverso da costante.

V invece è la velocità relativa tra due sistemi di riferimento inerziali qualunque e quindi è rigorosamente costante.

Credo che chiunque con due neuroni che si incontrano e che si salutano stringendosi le sinapsi, possa capire che una velocità generalmente non costante è diversa da una velocità rigorosamente costante.

Ora siccome sono io che interpreto in modo posticcio, concludo con l'articolo scientifico "On the Material Invariant Formulation of Maxwell’s Displacement Current" di Christo I. Christov (purtroppo deceduto nel 2012) del Dipartimento di Matematica (che quindi è stato un tuo collega matematico) dell'Università della Louisiana, pubblicato il novembre 2006, sul volume 36, issue 11, di Foundations of Physics (pp 1701–1717) e disponibile a questo link

www.christov.metacontinuum.com/My_Public...ov-Found.Phys.36.pdf

a pagina 1703 scrive una delle forme delle equazioni di Maxwell-Hertz e ne elenca alcune interessanti proprietà, che però non commento perché sprecato in questa discussione surreale



a pagina 1705 introduce le equazioni di Maxwell-Lorentz nell'interpretazione corrente



infine a pagina 1706 ci dice



surprise surprise, che le equazioni di Maxwell-Lorentz non si possono ridurre alle equazioni di Maxwell-Hertz perché nelle prime a velocità v è costante, mentre nelle seconde la velocità è arbitraria. Ti giuro che non ci vuole una laurea in matematica applicata per capire che V = cost e v <> cost sono due grandezze diverse, bastano i due neuroni ben educati di cui sopra.

Bene, anzi male, visto che ho perso altro tempo dietro ai tuoi vaneggiamenti. Onde evitare di farti spendere altro tempo nel rispondermi, ti dico subito che una tua eventuale risposta non verrà letta da me se, ad uno sguardo veloce, non ci sarà almeno un link ed uno screenshot ad un libro di fisica, con possibilmente delle frasi sottolineate che dimostrino che quel che ho detto è sbagliato. Se il tuo fine è quindi quello di convincermi con supercazzole evita perché sprechi tempo. Se il tuo fine è invece quello di auto-convincerti di avere ragione contro l'evidenza, magari tentando anche di convincere gli sfortunati lettori di questa pantomima, fai quel che ti pare, il tempo è il tuo....il mio l'ho già sprecato in abbondanza.

kamiokande ha scritto:

La forza F si trasforma sempre (always) con F' = R*F (equazione 2.10), dove R è la matrice rigorosamente ortogonale definita all'equazione 2.1 (di cui sopra), altrimenti la forza non avrebbe la stessa intensità in tutti i riferimenti inerziali.

Ti traduco quello che c'è scritto nel tuo link, usando la notazione dei commenti precedenti. Se F è una forza agente su un punto materiale e T una trasformazione di Galileo del sistema di coordinate, allora F(T(r))=R*F(r), per una certa R in SO(3) dipendente dalla trasformazione considerata. Come pronosticato non c'entra un accidenti di niente col fatto che T*F=T*G se e solo se F=G, cosa che vale sempre (always)*. In particolare l'equazione 2.10 si può riscrivere in forma equivalente come T*F'=T*R*F con T in GL(3,R) qualsiasi. Tanti saluti kamiokande.

*dimostrazione:

T*F=T*G <==> T*F-T*G=0 (uno spazio vettoriale è in particolare un gruppo)
T*F-T*G=T*(F-G) (T è lineare)
T*(F-G)=0 <==> F-G=0 (T è un isomorfismo ==> Ker T =0)

Picnic fra i campi vettoriali

Volendo dare un senso alla precedente discussione, dove è stata seminata più che altro confusione fra vettori e campi vettoriali, come fra algebra lineare e geometria differenziale, mi pare opportuno dare qualche informazione in più su questi oggetti matematici, la cui teoria è ricca di risultati inaspettati. Sono in effetti un tratto distintivo della matematica moderna, molte cose già note in precedenza trovano una giustificazine spesso semplice ed elegante usando l'approccio dei campi vettoriali (che si seminano nel terreno della geometria differenziale, è il caso di ricordarlo).

Più che dare una definizione formale, che chi è interessato può trovare facilmente nel web (state attenti alle imprecisioni della pagina italiana di wikipedia però, se mai scegliete quella inglese), meglio partire a bomba con un esempio pratico. Ragioniamo nel piano euclideo, che rappresenta il caso più semplice, poi generalizzeremo senza troppi problemi. Dunque un campo vettoriale nel piano R² è semplicemente una funzione R²-->R², ossia una funzione che ad ogni punto del piano associa un nuovo punto del piano. Siccome i punti del piano possono essere visti come vettori, cioè come freccette con la coda nell'origine del piano cartesiano e la punta nel punto considerato (mi si perdoni il calembour), questa funzione può essere rappresentata come un insieme di dette freccette sparse per tutto il piano, una per ogni punto. Si richiede anche che questa funzione abbia una certa regolarità, cioè innanzitutto che sia continua, e allora abbiamo un campo vettoriale continuo, e poi in genere che sia differenziabile un certo numero k di volte, cosa che definisce i campi vettoriali di classe C^k. In quanto segue daremo per scontata questa regolarità, come d'altronde accade spesso nella letteratura sull'argomento.

Allora dicevo che si parte con un esempio pratico, eccolo qua:



Come vedete abbiamo i nostri assi x e y e tante freccette*, che in questo caso seguono una logica piuttosto evidente: girano tutte in senso antiorario attorno all'origine degli assi. Per andare avanti è necessario introdurre la notazione propria dei campi vettoriali. Ce ne sono diverse a dire la verità, quella più semplice consiste nell'indicare il campo vettoriale V esplicitando le sue due componenti, che saranno funzioni di x e y, cioè:

V = ( v₁(x,y) , v₂(x,y))

Quindi v₁ e v₂ - che sono funzioni - sono le componenti del campo vettoriale, mentre x e y sono le coordinate del piano. Evidentemente le due cose non vanno confuse, ma quando si passa all'esempio pratico tutto si fa più chiaro, nel caso dell'immagine sopra infatti il campo vettoriale è dato da:

V = (-y , x)

perciò è semplicissimo, date delle particolari coordinate, trovare il vettore corrispondente (= freccetta uscente dal punto considerato), ad esempio al punto (x,y)=(1,0) corrisponde il vettore (v₁,v₂)=(0,1), al punto (1,1) corrisponde (-1,1), e così via. Si noti che al punto (0,0), l'origine, è associato il vettore nullo (0,0). Questo è l'unico punto in tutto il piano dove il campo V si annulla. In questo caso si parla di singolarità o punto critico, si tratta di punti fondamentali perchè danno informazioni molto importanti sul comportamento globale di V. Per capire il perchè bisogna introdurre un altro concetto associato ai campi vettoriali: quello di linea di flusso. Interpretiamo le freccette del campo come velocità istantanea relativa al punto considerato. Nel nostro campo particolare abbiamo ad esempio che nel punto (1,0) la velocità è (0,1), ora se immaginiamo una particella che si muove a partire da quel punto con la velocità data, ci domandiamo: dove andrà a finire se segue le freccette, sempre intese come velocità istantanea punto per punto?

Tecnicamente si tratta di risolvere un'equazione differenziale (ecco perchè parlavo di geometria differenziale...), ma senza addentrarmi in dettagli noiosi anticipo subito che nel nostro esempio le linee di flusso risultano essere circonferenze concentriche centrate nell'origine. Anzi, tutte le circonferenze concentriche centrate nell'origine. Dato un punto (x_p,y_p), la linea di flusso uscente da p è semplicemente la circonferenza di raggio |p|, ossia la distanza di p dall'origine. L'immagine seguente mostra alcune linee di flusso uscenti da diversi punti (evidenziati in rosso) di un campo vettoriale più complicato di quello da noi considerato:



Ora che abbiamo i concetti di punto critico (V=0) e di linea di flusso, possiamo enunciare un primo teorema generale sui campi vettoriali, il Teorema di Poincaré-Bendixson:

Se esiste una linea di flusso chiusa, allora c'è almeno un punto critico al suo interno.

Il nostro esempio è chiaramente una conferma clamorosa del teorema, dato che tutte le linee di flusso sono chiuse e contengono il punto critico nell'origine. Questo approccio permette un'analisi qualitativa relativamente semplice di situazioni che possono essere anche estremamente complicate: non serve avere l'espressione analitica del campo per capire se possiede singolarità, ci basta avere delle immagini come quelle sopra, seguire le freccette e vedere se le linee di flusso si chiudono o no. Attenzione: seguire le freccette significa tracciare la linea tangente ai vettori via via che si prosegue, cioè "seguire la via" indicata dalle freccette, non andare ad ogni passagio nel punto di arrivo della freccia, è bene precisarlo, ma adesso vedremo che la cosa è piuttosto scontata.

Infatti, sebbene da quanto detto finora sembrerebbe che tanto i vettori (v₁,v₂) quanto i punti (x,y) stiano nello stesso spazio, cioè il piano cartesiano, in realtà le cose non stanno esattamente così. Per capire il motivo è utile introdurre una prima generalizzazione dei campi vettoriali: i campi vettoriali definiti su superfici. La cosa funziona come prima, solo che adesso invece che avere freccette uscenti dai punti del piano le abbiamo uscenti dai punti di una superficie. Ecco nuovamente un esempio pratico, riguardante la sfera:



L'immagine è quella che è, non ne ho trovate di più belle, però dovrebbe essere chiaro il concetto: stavolta le nostre freccette sono vettori tangenti alla sfera. Per la precisione, in ogni punto della sfera, il vettore associato è un (unico) vettore del piano tangente nel punto stesso. Siccome anche il piano cartesiano è una superficie, dovrebbe iniziare a chiarirsi il perchè i singoli vettori non sono da considerarsi appartenenti al piano xy: sono in realtà, e in modo del tutto analogo a quanto succede con la sfera, vettori appartenenti a un nuovo piano con origine nel punto da cui parte la freccetta, quindi ogni vettore ha il suo piano personalizzato (anche qui, tecnicamente, si parlerebbe di fibrato tangente...).

I campi vettoriali sulle sfere permettono di dimostrare un interessante teorema, detto Teorema della sfera impettinabile (o "della palla pelosa", terminologia che per ovvi motivi preferisco evitare):

Non è possibile "pettinare" una sfera senza che si crei almeno una riga o una chierica.

Anche in questo caso è fondamentale il concetto di punto critico, più qualche nozione topologica che non posso approfondire, tuttavia siamo molto vicini alla situazione del teorema di Poincaré-Bendixson, nella fattispecie l'esistenza di un punto critico è garantita dalle proprietà topologiche della sfera (caratteristica di Eulero-Poincarè), e qui "punto critico" equivale a "chierica". Un corollario esotico del teorema è che, se consideriamo la circolazione dei venti dominanti sulla superficie terrestre, deve sempre esistere un punto singolare, cioè un ciclone o un anticiclone. La cosa non varrebbe se la terra avesse la forma di una ciambella, infatti una superficie torica è pettinabile:



Altro interessante teorema legato alla topologia della sfera e alla metereologia è il Teorema di Borsuk-Ulam, che si può enunciare in dimensione 1 o 2:

1 Sull'equatore esistono sempre due punti antipodali con la stessa temperatura.

2 Sulla terra esistono sempre due punti antipodali con stessa temperatura e pressione.

Solo la dimensione 2 è direttamente legata a campi vettoriali propriamente detti, la dimensione 1 riguarda invece i campi scalari, ma anche qui non voglio divagare troppo. Anzi, preferirei tornare al discorso iniziale, nato in qualche modo dalla discussione dei post precedenti. Come dicevo sopra occorre prestare attenzione alla differenza concettuale fra componenti del campo vettoriale e coordinate del sistema di riferimento. Nel nostro esempio queste erano rispettivamente (-y,x) e (x,y), ed è chiaro che non sono la stessa cosa (se non nel caso particolarissimo in cui x=y e x=-y, ossia x=y=0, cioè solo nell'origine). Il fatto è che se cambiamo sistema di coordinate possono succedere dei casini. Prendiamo per esempio la lungamente dibattuta trasformazione:

x'=k*x
y'=y

qui ristretta alla dimensione 2 (non cambia nulla), con k costante diversa da 0. Se sostituiamo le componenti di V abbiamo:

V = (-y,x) = (-y',x'/k)

Da cui risulterebbe:



Questo evidentemente non è lo stesso campo vettoriale V tracciato sopra (risulta "ovalizzato"), quindi nel cambio di coordinate qualcosa è andato storto. Per evitare simili inconvenienti, la notazione matematica standard per i campi vettoriali non è proprio quella che ho dato all'inizio, si scrivono piuttosto come somma (vettoriale, ça va sans dire) delle componenti moltiplicate per degli "strani" termini, che altro non sono se non la base dello spazio vettoriale in cui "vivono" le nostre freccette. Senza altri giri di parole si scriverebbe così:

V = -y ∂/∂x + x ∂/∂y

questi ∂/∂x e ∂/∂y (de-in-de-x, de-in-de-y) rappresentano nel nostro caso i due vettori-base (1,0) e (0,1), ma c'è un preciso motivo se si indicano in questo modo, non posso approfondire quanto vorrei ma basti vedere come si comportano quando cambiamo coordinate:

∂/∂x' =1/k* ∂/∂x
∂/∂y' = ∂/∂y

e perciò, sostituendo nell'espressione di V i termini non accentati con quelli accentati, si ricava:

V = -k*y' ∂/∂x' + x'/k ∂/∂y'

espressione che dà luogo allo stesso campo vettoriale mostrato dalla prima immagine (fate pure la prova sostituendo a ritroso le espressioni x',y',∂/∂x',∂/∂y' con le relative espressioni non accentate), e non poteva essere altrimenti dato che V è sempre lo stesso, indipendentemente dal sistema di coordinate in cui lo scriviamo. Si possono scegliere trasformazioni più esotiche, che mutano completamente l'espressione del campo, per esempio se scrivessimo V in coordinate polari, usando cioè le coordinate:

x = ρ cos φ
y = ρ sin φ

otterremmo l'espressione:

V = ∂/∂φ

Qui non deve trarre in inganno l'uso delle lettere greche ρ e φ per le nuove coordinate, ho solo preferito usare la notazione standard per non confondere, ma avrei potuto benissimo chiamarle x' e y'. Come si può notare, essendo V un campo che "gira" uniformemente attorno all'origine, in coordinate polari diventa un campo costante rispetto al "versore angolare" ∂/∂φ con componente nulla rispetto al "versore radiale" ∂/∂ρ.

Dopo aver affrontato una prima generalizzazione del concetto di campo vettoriale, dal piano a una superficie curva, passiamo alla generalizzazione dal piano allo spazio tridimensionale R³. In realtà non cambia quasi nulla, dobbiamo solo aggiungere una coordinata e una componente del campo vettoriale, che avrà quindi la seguente espressione generale:

V = ( v₁(x,y,z),v₂(x,y,z),v₃(x,y,z))

se usiamo la notazione con le sole componenti, oppure la relativa espressione come somma vettoriale che coinvolge anche i vettori della base:

V = v₁(x,y,z) ∂/∂x + v₂(x,y,z) ∂/∂y + v₃(x,y,z) ∂/∂z

Quest'ultima forma, detto per inciso, è usualmente abbreviata usando gli indici e la notazione di Einstein con V = vⁱ ∂/∂xⁱ, ma anche questo discorso ci porterebbe troppo lontano per essere approfondito. I nostri campi vettoriali in 3-d sono dunque un insieme di freccette, una per ogni punto dello spazio tridimensionale, che variano in modo continuo da punto a punto, insomma niente di diverso dal caso 2-d, se non che adesso abbiamo a che fare con entità proprie della fisica, perchè questi campi possono rappresentare campi gravitazionali, magnetici, elettrici, eccetera. Per arrivare ai campi E e B discussi sopra, rispettivamente elettrico e magnetico, manca ancora un'ulteriore generalizzazione: finora abbiamo considerato campi vettoriali statici, cioè indipendenti dal tempo, quando però sconfiniamo nella fisica matematica, in genere le quantità che analizziamo vanno considerate variabili nel tempo, e i campi vettoriali non fanno eccezione. Ecco allora che le componenti, oltre a dipendere dalle tre coordinate spaziali, dipendono anche da una nuova coordinata t, con l'ovvio significato di coordinata temporale.

I campi E e B risultano essere ciascuno una famiglia di campi vettoriali parametrizzati dalla coordinata temporale t. I campi vettoriali "statici" in questo modo diventano dei casi particolari, in cui al variare di t l'espressione del campo vettoriale resta sempre identica. Anche qui un esempio pratico può aiutare, questa l'espressione di un campo elettrico generato da una carica puntiforme posta nell'origine (0,0,0) dello spazio tridimensionale:

E = r/|r|³

con r=(x,y,z) e |r|=√(x²+y²+z²) (per chi fosse curioso usando la notazione di Einstein si scriverebbe E=(x_ixⁱ)^-3/2 * x^j ∂/∂x^j). Se la carica si muove, ecco che abbiamo un campo vettoriale variabile, dipendente dal parametro t, per esempio di seguito il campo della carica di prima che si muove lungo l'asse x con velocità costante:



L'espressione analitica di questo campo vettoriale si ottiene sostituendo nel campo vettoriale E alla coordinata x l'espressione x-v*t, dove il termine v rappresenta la velocità con cui si muove la carica. Notare che se la velocità v è uguale a zero si riottiene il campo statico dato prima, che corrisponde all'immagine centrale dell'animazione gif.

I cambiamenti di coordinate nel caso 3-d funzionano esattamente come con quelli 2-d, l'unica ovvia differenza è che c'è una coordinata z in più e un nuovo versore ∂/∂z da trasformare. I cambiamenti di coordinate che coinvolgono il tempo invece sono più delicati, perchè nella fisica classica il tempo è un parametro indipendente dal quadro di riferimento, nella fisica relativistica invece è una coordinata a tutti gli effetti, nè più nè meno come le tre coordinate spaziali, di conseguenza i due approcci richiedono metodi diversi e diversi sono pure i risultati, in generale.

Ma non ci occuperemo qua di tali argomenti, piuttosto se qualcuno è riuscito ad arrivare fino a questo punto, propongo un rapido test di verifica della comprensione. Supponiamo che all'inizio del post per dispetto invece che fornirvi le componenti del campo V esplicitamente, cioè invece che dirvi che:

v₁ = -y
v₂ = x

vi avessi fornito le seguenti uguaglianze:

k*v₁ = -k*y
v₂ = x

con k solita costante arbitraria diversa da zero, come andrebbe modificato il discorso che riguarda il campo V=(v₁,v₂)? Potete scegliere fra le seguenti risposte, nello spoiler la soluzione:

1) Non cambierebbe niente perchè le due coppie di uguaglianze sono del tutto equivalenti.
2) Questa non è una verifica della comprensione perchè la domanda non c'entra un accidenti con i campi vettoriali.
3) Il campo V è in questo caso diverso, così come tutto il discorso seguente, anche se in modi imperscrutabili.



*Per ragioni di chiarezza delle immagini i vettori sono riscalati logaritmicamente, le freccette tendono quindi ad avere una lunghezza minore e più uniforme rispetto a quella reale.