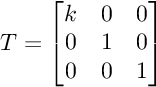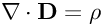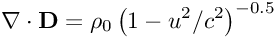- Messaggi: 850
- Ringraziamenti ricevuti 118
La formula del latte è Vacca2O
Preciso subito che il titolo è una citazione di Bergonzoni, il motivo per cui l'ho scelto è che intendo presentare alcune vaccate che si possono leggere in contesti nei quali ci si aspetterebbe precisione da parte dell'autore. Nel discutere gli errori si dovrebbe trovare una certa comprensione dei concetti sottostanti e magari en passant ci sarebbe la possibilità di farsi un'idea non preconcetta del perchè il rigore è necessario ma non preclude la fantasia.
Veniamo ad un primo esempio pratico, per capire dove voglio andare a parare. Questa scansione è tratta dal libro La macchina del mondo di Antonio Clericuzio, è un testo inserito nei corsi universitari di Storia della Scienza e dunque ci si attende una buona dose di precisione, ecco cosa dice a proposito della sezione aurea:
Non serve essere molto addentro la materia per accorgersi che in poche righe c'è un coacervo di errori difficile da stipare in uno spazio tanto piccolo. Partiamo dal più evidente: un innocuo errore di stampa, nella frase sottolineata bisogna evidentemente sostituire 1,618 a 0,618, e questo lo abbuoniamo volentieri, ma applicando la correzione leggiamo comunque:
...e qui di magagne ce ne sono parecchie. Innanzitutto 1,618 non è un numero irrazionale, tanto è vero che per esempio 1,618=1618/1000 ( i numeri irrazionali sono quelli che non possono essere espressi sotto forma di frazione, come radice di 2 o pi greco). Ovviamente pure qui c'è un refuso, anche se in questo caso non mi sento di assolvere l'autore senza ulteriori analisi, perchè la scrittura corretta è 1,618... e quei tre puntini fanno una bella differenza: significano che le cifre proseguono indefinitamente senza che vi sia un particolare ordine di ricorrenza.Moltiplicando 1,618, che è un numero irrazionale, per la lunghezza del segmento dato, si ottiene la misura della sezione aurea...
Qualcuno potrebbe subito obiettare: "ma sì, dai, alla fine cosa cambia?". Cambia parecchio, primo perchè per un matematico leggere una cosa del genere è come per un letterato leggere:
Proseguiamo correggendo quest'ulteriore, ben più grave, errore. La frase non è ancora giusta: non è vero che bisogna moltiplicare questo valore per la lunghezza del segmento AB (cioè a+b) per ottenere la sezione aurea, perchè questa è già la sezione aurea. Per sezione aurea infatti si intende quel numero, in genere indicato con phi, radice positiva dell'equazione:
Confrontando la proporzione qui sopra con quella presente nel libro ci si accorge di un ulteriore grave errore presente nella pagina: se risolvi l'equazione
a2-ab-b2=0
rispetto all'incognita "a" nella soluzione deve comparire l'incognita "b", a meno che tu non ponga b=1 (e nel caso dovresti avvertire il lettore), cosa che ci porterebbe dritti all'equazione considerata da noi (ponendo a=phi) e con ciò non avrebbe più senso moltiplicare il risultato per la lunghezza del segmento AB, che tra l'altro verrebbe ad essere a+1.
Mi ripeto: tutto ciò può apparire un inutile eccesso di rigore, ma dal punto di vista tecnico non è più eccessivo della richiesta di rispettare le regole grammaticali e l'ortografia in un testo scritto. Si può soprassedere, ma viene fuori una schifezza.
**********************************
Altro esempio, stavolta più "alternativo", non tanto per la sostanza quanto per la fonte. Sto parlando infatti del libro Contattismi di massa dello scomparso Stefano Breccia, in cui si raccontano vari casi di contattismo fra i quali quello italiano noto come "amicizia" in cui Breccia fu coinvolto direttamente. Nell'appendice che propongo si parla comunque di triangoli. L'autore, ingegnere elettronico, propone la seguente "dimostrazione" del teorema che afferma che tutti i triangoli sono equilateri:
Non è strettamente necessario leggere e capire l'argomentazione per analizzare la parte sottolineata, anche se sarebbe utile. Ha ragione Breccia quando dice che quella presentata, con la dovuta (e mancante) introduzione, sarebbe una dimostrazione per assurdo che il punto D non può stare all'interno del triangolo, è però sbagliato tutto il resto. Per prima cosa la dimostrazione è perfettamente in linea con lo stile di Euclide, quindi non è riservata ai moderni, ma più importante di questo è il fatto che il baco della dimostrazione non sta affatto dove lo pone l'autore. D'altronde Euclide non era certo uno sprovveduto e sapeva benissimo formalizzare la differenza fra interno ed esterno di un triangolo, evidentemente il baco è un altro e non ha niente a che fare con i concetti di interno ed esterno.
Per capire dove sta bisogna comprendere il processo stesso di dimostrazione matematica. In questo caso è presentata una "dimostrazione" (tra virgolette perchè è sbagliata) di tipo sintetico, vi è poi un altro schema generale di dimostrazione definita analitica. Sappiamo tutti che sintetico significa in questi casi "che va dal particolare al generale", ci mettiamo quindi in un caso specifico, cioè quello della figura, e poi una volta condotta la dimostrazione ragionando su questa concludiamo che vale per ogni caso data l'arbitrarietà della figura. Va da sè che se la figura non è precisa, o non è arbitraria, la dimostrazione non è valida. In questo caso la figura è sbagliata, cioè non esiste la configurazione ipotizzata, quindi, essendo la premessa implicita della dimostrazione "poniamoci in questo caso particolare (e reale)", risulta falsa la premessa e dunque a partire da questa si può concludere tutto e il contrario di tutto (ex falso quodlibet*), e tra le varie cose anche che tutti i triangoli sono equilateri.
Visto che l'ho nominata mi pare il caso di dire come funzioni una dimostrazione analitica, e qui concludo questo primo intervento. Anche qui è noto che analitico sta per un ragionamento "che va dal generale al particolare", in ambito matematico si intende una dimostrazione che per esempio parte da un'uguaglianza algebrica universalmente valida, come potrebbe essere (a+b)2=a2+2ab+b2, e da questa deriva un risultato particolare, anche qui per fare un esempio stupido potremmo dimostrare che, se a>b, allora l'area del quadrato di lato a+b è maggiore della somma a2+3b2, cioè dell'area del quadrato di lato a più tre volte l'area del quadrato di lato b. Mi fermo qui.
* A questo proposito, in un commento su questo sito , riportavo la "spassosa" dimostrazione di Bertrand Russell del "teorema: se 2+2=5 io sono il papa".
FranZη
Si prega Accesso a partecipare alla conversazione.
- Tizio.8020
-

- Offline
- Utente
-

- Messaggi: 52
- Ringraziamenti ricevuti 1
Dal momento che non me ne ricordo, semplicemente NON è Papa.
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
L'immagine è presa da facebook quindi non son nè chi sia l'autore della domanda nè quello della simpatica risposta, che comunque anticipo subito non è da considerarsi scorretta. In effetti non abbiamo abbastanza informazioni su Carlo per poter rispondere adeguatamente, come vi potrete convincere se mi seguite un momento.
Poniamo che Carlo sia un ragazzino che sta studiando le espressioni algebriche, altrimenti note come "espressioni" tout court e notoriamente incubo di molti adolescenti. In tal caso non c'è dubbio che si stia sbagliando di grosso perchè in nessun caso si può interpretare y2 come variante di 2y, sono accettabili le forme y*2 o y x 2 (dove x sta per la moltiplicazione, in questo caso essendoci già una x come incognita è meglio evitare quest'ultima variante), in ogni caso è buona norma nelle espressioni algebriche anteporre il coefficiente numerico all'incognita senza alcun segno per la moltiplicazione, in definitiva l'uguaglianza corretta sarebbe:
Ma abbiamo anche un'altra possibilità, e qui arriva la parte complicata del discorso. Carlo potrebbe essere un fine analista, nel senso dell'analisi matematica, e allora la sua affermazione è molto più difficile da verificare. Innanzitutto, da analista scafato, Carlo sottointende le scritture:
In questo caso particolare ho tracciato in rosso la funzione y(x)=x^2 e in blu la funzione y(x-2)=(x-2)^2, è abbastanza evidente che la seconda ha lo stesso grafico della prima, solo spostato di due unità verso destra. Torniamo a Carlo e vediamo di capire cosa accidenti cerca di dirci con l'espressione:
Ora se sono riuscito a spiegarmi dovreste convenire che, nel caso in cui Carlo non sia uno scolaretto sprovveduto ma un matematico scafato, la sua espressione è perfettamente lecita e propone un problema tutt'altro che banale. Insomma, hai voglia di capire se ha ragione o no...anche perchè qui sopra ho riportato solo le equazioni corrispondenti a due valori particolari di x, ma in realtà per risolvere il problema di Carlo bisogna risolvere le infinite equazioni che si ottengono sostituendo ad x ogni valore che potrebbe avere, cioè ogni numero reale. Un bel casino.
Sicuro che se vi lascio così stanotte non riuscireste a dormirci adesso vi spiego come ho pensato di risolvere la questione. Si tratta comunque di una soluzione particolare, la soluzione generale non mi metto nemmeno a cercarla.
Ho usato la funzione Gamma di Eulero che ha la proprietà:
*********************
@Tizio.8020
Penso che la tua fosse una battuta, ma ti giuro che non l'ho capita...
FranZη
Si prega Accesso a partecipare alla conversazione.
- Tizio.8020
-

- Offline
- Utente
-

- Messaggi: 52
- Ringraziamenti ricevuti 1
Era parte di una vecchissima barzelletta.
Un Ispettore del Ministero della Sanità si reca a visitare un manicomio, ed il Direttore gli mostra le varie sezioni in cui sono divisi i pazienti.
Vedono la sezione in cui tutti i Napoleone discutono fra loro, quella dei furiosi, quella dei tranquilli, poi entrano in un'altra , in cui diversi pazienti discutono fra loro ad alta voce.
L'ispettore chiede di cosa mai stiano discutendo così animatamente, sembrano veramente infervorati.
Il Direttore risponde che tutti sostengono di essere il Papa, e quindi non si mettono d'accordo su chi lo sia e chi no.
Chiedono quindi ai pazzi di spiegarsi.
<Io sono il Papa! Ho vinto il Conclave!!!> dice il rpimo
<IO sono il Papa, tu sei morto ed hanno eletto me!!> dice il secondo.
<Non è vero: IO sono il Papa, me l'ha detto Dio!!!> urla il terzo.
<<Cosa t'avrei detto io? Ma se non ti ho mai visto prima! Se avessi fatto Papa un pazzo, me ne ricorderei bene!!!>> ribatte seccato l'Ispettore...
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Nota a margine: tempo fa in un commento su questo sito spiegavo come avessi disdetto l'abbonamento a Le Scienze a causa di una serie di articoli di Odifreddi e della presenza fissa di una rubrica di Attivissimo. Sto pensando di rinunciare anche a quello a S.A. dato che presenta una rubrica equivalente e da un po' di tempo non permette più di commentare gli articoli online. A dirla tutta non permette nemmeno più di accedervi, se non dietro pagamento di un ulteriore abbonamento.
Nota a margine alla nota a margine: di Odifreddi poi magari ne parleremo un giorno...
Veniamo all'articolo che voglio proporre: Math Explains Likely Long Shots, Miracles and Winning the Lottery , ovviamente è in inglese ma faccio io un riassuntino. Rientra grossomodo nella categoria "ecco come cerchiamo di dimostrarvi matematicamente che le coincidenze sono solo il frutto della vostra immaginazione, brutti beoti ignoranti (e magari pure complottisti)". Inutile dire che l'autore non si avvicina nemmeno lontanamente al suo scopo.
L'incipit è una dichiarazione programmatica: l'autore introduce un fantomatico "Principio di Improbabilità" (ovviamente di sua invenzione) che ci assicura basato su un insieme di leggi matematiche, come spiegazione ultima delle coincidenze. Segue un primo esempio che rappresenta un classico evergreen di tutti i corsi di calcolo delle probabilità. Siamo in una stanza affollata, con quante persone presenti sareste pronti a scommettere (alla cieca ovviamente) che due a caso condividono lo stesso compleanno? Di primo acchito la risposta sembrerebbe essere che la stanza deve essere veramente affollata, almeno 183 persone stipate se voglio avere più probabilità di vincere che di perdere, ma come avrete già intuito è una risposta profondamente sbagliata. Tenetevi forte perchè ne bastano 23. La probabilità cercata è infatti, con n persone nella stanza:
Esaurito l'esempio da festa delle medie ecco che si entra nel vivo:
Il 6 settembre 2009 la lotteria bulgara ha estratto casualmente i sei numeri 4, 15, 23, 24, 35, 42.
...
Ciò che è sorprendente è quello che è successo quattro giorni dopo: la lotteria bulgara ha estratto casualmente come numeri vincenti 4, 15, 23, 24, 35, 42 -esattamente quelli della settimana precedente.
Fin qui la fredda cronaca, ora inizia la manfrina sul Principio di Improbabilità, seguendo le argomentazioni:
1) molte lotterie vengono organizzate in tutto il mondo;
2) queste proseguono indefinitamente nel tempo, anno dopo anno;
3) la legge delle combinazioni [quella sul numero delle possibili coppie, NdT] fa il suo corso: ogni volta che c'è un'estrazione, i numeri estratti possono coincidere con i numeri di qualunque estrazione precedente [...e poi giù ancora con la formula del numero di coppie possibili NdT].
L'articolo prosegue:
La lotteria bulgara estrae 6 numeri su 49, il che porta il numero di combinazioni per ogni estrazione a c=13983816, ciò comporta che la probabilità che due particolari estrazioni coincidano è 1/c (cioè circa una su 14 milioni). Ma cosa si può dire sulla probabilità che due estrazioni qualsiasi coincidano?
Da qui in poi parte una serie di elucubrazioni sulle varie possibilità di combinare diverse estrazioni di una lotteria. Non le riporto perchè non spiegano niente. Manca infatti l'unica, vera, ovvia analisi su quanto appena detto: qual è la probabilità che si verifichi l'evento della lotteria bulgara?
Se caricate i commenti all'articolo, ordinati dai più vecchi, mi trovate (curiosità: il mio nickname su LC è preso da quello di SA, mi sono iscritto qui più o meno nel periodo in cui commentavo l'articolo), ed espongo la stessa perplessità sollevata qui sopra: dov'è l'analisi del caso bulgaro? Non preoccupatevi: ci ho pensato io! Ecco cosa scrivevo nel mio primo commento:
Scherzo dai, dimenticatevi il grassetto, il commento originale proseguiva così:Cit.:"Il risultato della lotteria bulgara è insolito per il fatto che le due identiche estrazioni sono consecutive."
E grazie, Graziella e grazialcazzo! Era proprio questo che dovevi spiegare, se ne eri capace!
Penso che questa affermazione meriti un'analisi più appropriata. La cosa stupefacente nella lotteria bulgara è proprio il fatto che le due estrazioni sono consecutive. Se non lo fossero state, probabilmente non se ne sarebbe accorto nessuno, o al limite sarebbe rimasta una curiosità marginale.
Ora, il numero medio di estrazioni necessario perchè una cosa del genere avvenga (due estrazioni consecutive identiche nella lotteria bulgara) è 13983817. Si tratta del numero di combinazioni più uno.
...
Ora dividiamo questo numero per 104, il numero di estrazioni in un anno, il risultato è circa 134460 anni, questo è il tempo medio che dovremmo attendere per vedere quello che si è effettivamente verificato. A me sembra davvero stupefacente!
Per chi fosse curioso riporto nello spoiler un commento successivo, in cui spiegavo come ero arrivato al "numero di combinazioni più uno". E' in inglese ma suvvia, si capisce...non fatemi tradurre!
1) E(X)
 (1/p)^k)*(1/q)-(1/q)
(1/p)^k)*(1/q)-(1/q)where:
X is the random variable "number of trials in a Bernoulli process to get k consecutive successes"
p is the probability of success and q=1-p .
(So if p=q=1/2 and k=2 we have the average number of tosses to get HH: 4*2-2=6)
For k=2 1) becomes:
2) E(X)=(1+p)/(p^2)
this is the average number of trials to get two consecutive successes in a Bernoulli process, and it is also the average number of draws to get two consecutive time the same fixed combination of numbers in a lottery. But the same sequence of draws can be ragarded as c=1/p different Bernoulli processes, one for each possible combination c. In other words: on average, after the number E(X) given by 2) of draws, each possible combination of the lottery can appear twice in a row. Thus we can conclude:
3) E(Y)=E(X)/c=1+1/p=1+c
where Y is the random variable: "number of trial to get two consecutive times the same (not fixed) combination in a Bulgarian-like lottery".
1) is a well-known formula, 3) is a my own derivation (because in the article was missing!) and, if correct, it should be known as well, while "Bernoulli law" is a mistranslation due to my bad english.
PS E(X) indica la media della variabile casuale X.
************************
@Tizio
Ok, ora ho capito la battuta.
FranZη
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Il primo input, c, è il numero di combinazioni della lotteria, il secondo, n, è il numero di simulazioni successive che si intende fare. In pratica il computer inizia a simulare estrazioni, finchè non ne ottiene due successive uguali, conta il numero di estrazioni necessarie e ripete il tutto n volte, da ultimo fa la media di tutti i numeri di estrazioni ottenuti. Dato che si tratta di verificare che il numero medio di estrazioni per ottenerne due identiche consecutive è uguale al numero delle combinazioni più uno, cioè c+1, più prove si fanno più ci avviciniamo al valore teorico, quindi maggiore è il numero n meglio è...è la statistica, baby!
Simulare le estrazioni della lotteria bulgara, con circa 14 milioni di combinazioni, non è una cosa che un computer accetta di buon grado*, si può partire quindi dal lancio di una moneta, con due combinazioni, o dal lancio di un dado, con 6:
In questo caso il numero di simulazioni è 10000 e come si può verificare si ottengono valori vicini a quello teorico. Per induzione possiamo stare tranquilli che la formula è valida per ogni numero intero, anche per quello delle combinazioni della lotteria bulgara, tantopiù che per numeri di quelle dimensioni non fa alcuna differenza che il numero cercato sia effettivamente "il numero delle combinazioni più uno" o semplicemente un numero dello stesso ordine di grandezza di c.
Per chi invece volesse provare con Matlab -non state nella pelle, lo so- qui c'è lo script apposito:
* Anche perchè se vogliamo un risultato statisticamente rilevante dovremmo prendere n molto maggiore di c. Io però che ho un computer cazzuto ho provato a fargli simulare 10 volte la lotteria bulgara, con c=13983816 e n=10 ha dato come risultato 18 milioni circa, non è vicino al c+1 della teoria però è dello stesso ordine di grandezza di c come ci si doveva aspettare.
FranZη
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Questa volta prendo spunto da un vecchio commento trovato qui su luogocomune, sul vecchio sito per la verità. Dato che non ho alcuna intenzione di discutere l'argomento originale, ma solo le affermazioni prettamente matematiche, credo che non sia necessario citare nè la fonte originale nè l'autore, che a quanto mi pare di aver capito non frequenta più il sito da tempo. Per ragioni analoghe non sto nemmeno a spiegare come sia finito a leggere quel particolare commento, poi se necessario potrò dare più dettagli. Il tema è nientemeno che l'infinito.
Stop. Fermiamoci un attimo a riflettere. Non mi interessa minimamente qui discutere di scie chimiche quindi non mi metto nemmeno a contestare il fatto che note pressione, umidità e temperatura, della quota potremmo anche fregarcene, ma visto che è stata nominata allora diciamo che anche la quota non varia da -infinito a + infinito. Quindi l'ultima affermazione è perlomento ambigua, visto che i NUMERI REALI variano proprio da -infinito a + infinito, infiniti esclusi, dunque se mai queste grandezze appartengono ad un sottoinsieme dei numeri reali.L'insieme dei Sapiens Sapiens, nel corso di - almeno - 500 anni di SCIENZA, si è prodigato ogni giorno per elaborare MODELLI MATEMATICI atti ad ANALIZZARE e PREDIRE le condizioni di:
- Umidità;
- Pressione;
- Temperatura;
- Quota (altezza dal suolo);
In cui si formano SCIE DI CONDENSA.
Sono 4 VARIABILI FONDAMENTALI - ognuna delle quali ha la CARDINALITA' DEL CONTINUO.
Per Cardinalità si intende il numero di possibili valori che può assumere una grandezza: per esempio il BIT ha cardinalità 2 (può assumere solo i valori di 0 e 1)
L' insieme definito CONTINUO ha cardinalità INFINITA (ossia sono possibili infiniti valori)
Certo: nè temperatura, nè pressione, nè umidità variano da +infinito a -infinito.
Ma tutte e 4 le suddette GRANDEZZE FISICHE appartengono all'insieme dei NUMERI REALI.
Questo non inficia quanto viene detto dopo, ossia che l'insieme dei possibili valori di queste grandezze fisiche ha la cardinalità del continuo perchè, strano a dirsi, ma ogni intervallo aperto (a,b) di numeri reali ha la cardinalità del continuo, ossia ci sono tanti numeri reali tra - infinito e + infinito di quanti ce ne sono per esempio tra 0 e 1 (o tra 0 ed epsilon con epsilon piccolo a piacere). Questo è ancora niente perchè si può dimostrare in mezza riga che esistono tanti numeri pari quanti numeri naturali, ma ne parliamo dopo. Però se mai si potrebbe obiettare che i modelli matematici di cui si parla qui sopra sono necessariamente implementati al computer, e il computer fa i conti con i numeri macchina (espressi in bit ça va sans dire) che sono un sottoinsieme finito dei numeri razionali, a loro volta sottoinsieme dei reali, quindi scomodare il continuo in questo contesto non ha senso. Però come ripeto non sono interessato all'argomento ma all'argomentazione quindi passo oltre. Vediamo dove si va a parare:
Allora qui si dice che dal punto di vista scientifico matematico è corretto dire che esistono infinite combinazioni di valori delle quattro grandezze fisiche in questione in corrispondenza dei quali si possono formare scie di condensa. Anzi no, non sono infinite ma sono tante, proprio tante. Io che non voglio parlare di scie chimiche cerco solo di capire l'argomentazione. Su quali basi sono tante? E su quali sarebbe corretto dire che dal punto di vista scientifico matematico sono addirittura infinite? A quanto pare sulla base di quanto citato in precedenza, cioè che ognuna delle quattro variabili può assumere infiniti valori, anzi, l'insieme di definizione di ognuna ha la cardinalità del continuo.Con quanto detto potrei uscirmene dicendo che sono possibili INFINITE COMBINAZIONI di VALORI di:
- Umidità;
- Pressione;
- Temperatura;
- Quota (altezza dal suolo);
In corrispondenza dei quali si possono FORMARE SCIE DI CONDENSA.
Eppure, se ti dicessi che tali combinazioni sono INFINITE - pur essendo nel giusto dal punto di SCIENTIFICO/MATEMATICO - sarebbe come se cercassi di truffarti al pari degli sciacomici.
Tali combinazioni non sono INFINITE... ma sono TANTE... TANTE... proprio TANTE...
Quando si scomodano gli infiniti, addirittura col loro nome proprio, bisogna fare attenzione perchè la stronzata è dietro l'angolo. Eh sì, perchè di infiniti non ce n'è mica soltanto uno...ma andiamo con ordine: parliamo del continuo. Normalmente su un'auto abbiamo diversi strumenti analogici: il tachimetro (velocità), il contachilometri (in effetti adesso sono comuni quelli digitali, però il vecchio tipo con le cifre sulle rotelline si può considerare analogico), il contagiri e il termometro dell'acqua sono i più comuni, i primi due sono proprio obbligatori ma sono abbastanza certo che abbiate visto tutti anche gli altri due. Bene, questi strumenti misurano grandezze fisiche che possono assumere tutti i valori reali in un certo intervallo, ossia per ognuna possiamo invocare la cardinalità del continuo. Questo dimostra in qualche modo che esistono infiniti valori di queste grandezze per cui si possa viaggiare in terza a 180 all'ora? Appunto...
...Però basta che ci sia un valore particolare che soddisfa la condizione, perchè ce ne siano automaticamente infiniti. Poniamo che la vostra auto (presumibilmente una Lamborghini) raggiunga davvero i 180 km/h in terza, avremo allora il tachimetro che segna 180, il contagiri che so, 7000 giri, mentre il contachilometri può segnare un valore a piacere fra quelli ammissibili e anche il range della temperatura dell'acqua può variare in modo continuo. Ma il punto è che basta anche un range minimo di variazione per far si che i valori compresi in quell'intervallo abbiano la cardinalità del continuo.
Ma poi fa qualche differenza, in quest'ottica, che le grandezze siano 4 invece di 1, o che non siano 1000? Assolutamente no. Se le nostre 4 grandezze fisiche potessero assumere solo n valori, con n numero naturale (0,1,2,3,..) i possibili valori combinati di 4 grandezze sarebbero n4, quindi con 2 possibili valori avremmo 16 combinazioni, e con 10 valori 10000 combinazioni. Si potrebbe immaginare dunque che avendo per ognuna c possibili valori (c indica la cardinalità del continuo) si ottenga un numero di combinazioni enorme. Altro che quello che a volte si definisce una cifra, altro che lo sbanderno (è il numero più alto dell'Emilia Romagna), molto più di tanto ma tanto féss (è la quantità più alta che si conosca a Brescia e provincia)...ma molto oltre anche l'ordine di grandezza di millemila perchè, qualunque valore vogliate dargli, esiste sempre millemila+1. Invece c+1=c!
Non solo, vale anche c*c=c, da cui si deduce che per quanto riguarda il nostro caso c4=c (in realtà qualunque sia l'esponente n vale cn=c), perciò non fa alcuna differenza considerare una o quattro variabili con la cardinalità del continuo, dal punto di vista del numero di combinazioni possibili. Questo fatto ha anche conseguenze curiose in geometria: data l'identificazione che esiste fra numeri reali e punti di una retta (si parla di "retta numerica", due rette numeriche sono per esempio i due assi perpendicolari del piano cartesiano), risulta che su una retta ci sono tanti punti quanti in un piano o nello spazio n-dimensionale. Ragionando su intervalli limitati si può affermare che lo spigolo di un cubo contiene tanti punti quanti una faccia o il cubo intero.
La cosa può sembrare una masturbazione mentale al limite del TSO, ma invece è matematica rigorosa tanto quanto l'aritmetica. Per convincersene occorre capire come si fa a dire che un infinito è uguale o diverso da un altro. Come spesso accade si usa un'estensione plausibile di una regola nota in un un caso particolare. Per verificare se due insiemi finiti hanno lo stesso numero di elementi basta contarli e controllare se i due numeri naturali coincidono. Ma se gli insiemi sono infiniti non si può contare il numero degli elementi, perchè quello che noi chiamiamo "numero" è sempre minore di infinito. Questo è il motivo per cui qui sopra ho sempre cercato di evitare di parlare di "numero di punti di una retta" rispetto al "numero di punti di un piano", ma ho solo detto che "sono tanti quanti". Infatti abbiamo un altro modo per confrontare il numero di elementi di due insiemi: usare le funzioni fra i due insiemi.
Partiamo dagli insiemi finiti per vedere come si generalizza il procedimento a quelli infiniti. Servono tre semplici concetti che sicuramente avrete incontrato almeno una volta a scuola, sto parlando delle funzioni iniettive, suriettive e biettive. Ricordando che una funzione da un insieme X a un insieme Y è un insieme di coppie (x,y) dove x appartiene a X e y a Y con la proprietà che per ogni elemento x0 di X esiste una e una sola coppia (x0,y) appartenente alla funzione*, ecco di seguito le definizioni di funzione -
-iniettiva: ogni y è in relazione con al più un elemento x;
-suriettiva: ogni y è in relazione con almeno un elemento x;
-biettiva: la funzione è sia iniettiva che suriettiva (in tal caso si parla anche di corrispondenza biunivoca fra gli insiemi X e Y).
Se gli insiemi X e Y hanno un numero finito di elementi, diciamo rispettivamente nx e ny, è facile verificare che data una funzione y=f(x) fra i due insiemi risulta che:
-se f è iniettiva allora nx è minore o uguale a ny;
-se f è suriettiva allora nx è maggiore o uguale a ny;
-se f è biettiva allora nx=ny.
Ecco quindi un modo plausibile per estendere il concetto di cardinalità (è il numero degli elementi di un insieme) ad insiemi infiniti: diciamo che la cardinalità di X è uguale a quella di Y se esiste una funzione biettiva fra i due insiemi. Se non esiste i due insiemi hanno cardinalità diversa, per stabilire quale sia la maggiore si usano gli altri due tipi di funzioni. Vediamo allora come stanno le cose rispetto agli insiemi numerici più importanti, che ricordo sono:
- N numeri naturali: 0,1,2,...
- Z numeri interi: ...,-2,-1,0,1,2,...
- Q numeri razionali: le frazioni m/n con m e n numeri interi
- R numeri reali: tutte le successioni di cifre decimali a virgola mobile finite, infinite periodiche o non periodiche**
La risposta è negativa ed è un famoso e sorprendente risultato noto come Teorema di Cantor , vi consiglio di dare un'occhiata al link per apprezzare la semplicità ed eleganza della sua dimostrazione. Il teorema stabilisce che la cardinalità dei numeri reali è strettamente maggiore di quella dei naturali, quindi esistono almeno due infiniti diversi: la cardinalità di N che si indica con א 0 (aleph-0, l'indice andrebbe a destra ma la lettera aleph ha mandato in tilt il sistema che crede voglia scrivere da destra a sinistra) e la cardinalità di R -o del continuo- che come già detto si denota con c.
Allo stato attuale di conoscenza sappiamo che c=2א e che se i è un infinito allora 2i è un infinito strettamente superiore, il che comporta l'esistenza di infiniti infiniti. La questione se esista una cardinalità infinita compresa tra א (rinuncio allo 0!) e c si è rivelata uno dei problemi più formidabili dei fondamenti della matematica, l'ipotesi che non esista è nota come ipotesi del continuo ed è stata formulata dallo stesso Cantor. In tempi piuttosto recenti si è dimostrato che tale ipotesi è indipendente dagli assiomi della teoria degli insiemi, cioè si è riproposta la situazione del postulato delle parallele negli assiomi di Euclide: in quel caso l'indipendenza porta all'esistenza di geometrie non euclidee, mentre nel caso dell'ipotesi del continuo porta a una sorta di biforcazione della teoria matematica, che procederà su due rami diversi, uno che accetta l'ipotesi e l'altro che la rigetta.
*In realtà la definizione formale di funzione è leggermente diversa, quella che ho dato è la definizione di grafico di una funzione, ma non voglio appesantire troppo.
**Anche qui la definizione formale è più complicata ma a noi va bene questa.
FranZη
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
L'altro giorno una mailing list a cui sono iscritto invia una mail sulle criptovalute, ecco di seguito un breve estratto:
...
L’articolo di Bloomberg riporta che il prezzo edgeless è aumentato del 500%, ma si riferisce SOLO alla rivalutazione del suo prezzo ufficiale di listino…
Bloomberg NON dice di quanto è stato rivalutato edgeless da quando è stato offerto la prima volta nella sua ICO.
Questo calcolo può farlo solo chi ha davvero partecipato all’ICO…cioè noi!
...
All’ICO di edgeless, i nostri abbonati hanno comprato questa valuta a un prezzo che si aggirava intorno a 0,00071 ethereum (circa 0,0000286 bitcoin di allora).
Già quando edgeless è stato quotato la prima volta in un mercato ufficiale, lo si poteva rivendere a circa 0,000118 bitcoin.
Attento: nell’ultimo prezzo citato c’è uno zero in meno rispetto al prezzo iniziale riportato più sopra! Quindi la differenza tra prezzo di ICO e prezzo iniziale a mercato di edgeless era già del 300% circa (parlo della percentuale di incremento che c’è tra 0,0000286 e 0,000118 bitcoin).
Ciò significa che ad esempio, non appena edgeless è stato quotato sul mercato potevi già vendere il 10% degli edgeless guadagnati all’ICO per rientrare sull’investimento iniziale (in questo modo avevi la tranquillità necessaria per conservarti la maggior parte degli edgeless in attesa che il suo valore aumentasse ancora).
In seguito, come dice Bloomberg, edgeless è aumentato del 500%, che in termini di ICO corrisponde a un guadagno dell’800% (cioè il 300% rispetto all’ICO iniziale + il 500% rispetto al prezzo di listino).
La sottolineatura è mia e se avete fatto attenzione ne avrete già intuito il motivo. Riassumiamo: la criptovaluta edgeless viene inizialmente lanciata tramite una ICO (Initial Coin Offer) ad un pubblico ristretto, poi in seguito viene messa sul mercato aperto a tutti. Poniamo per semplicità che il valore iniziale di edgeless fosse 1, nel tempo trascorso fino al lancio definitivo sul mercato la criptovaluta si era già rivalutata del 300%, poi il mercato la rivaluta di un ulteriore 500%, quindi la rivalutazione totale è...
...2300%!!!
Cioè il valore finale di edgeless è 24, rispetto all'1 iniziale. Nella mail c'è evidentemente un errore madornale, insito nell'uso delle percentuali, poi come se non bastasse c'è anche un vizio minore che spiego subito. Le percentuali sono utili perchè siamo bene o male tutti abituati ad interpretarle intuitivamente, questo però nel caso in cui si usino valori tra 0% e 100%, eventualmente anche negativi. Ma per valori superiori al 100% diventa molto più comodo usare i moltiplicatori: 2x, 3x, 4.34x...perchè dire che c'è un aumento del 300% o del 500% significa rispettivamente 4x e 6x, solo che la scrittura coi moltiplicatori è molto più chiara.
Veniamo all'errore madornale: in genere le percentuali non si sommano. Prima di approfondire mi sembra il caso di chiarire cosa sia una percentuale, anche se può sembrare ovvio, repetita iuvant. Una percentuale è il numeratore di una frazione che ha per denominatore 100 (da cui il nome: il 10% in forma decimale si scriverebbe 0.1, e in effetti 10=0.1*100), con una piccola clausola: mentre una frazione rappresenta un numero di per sè una percentuale è sempre relativa ad un valore di riferimento. Quindi il 10% non significa niente se non specifichiamo il 10% di che cosa. Ora torniamo all'errore nella somma delle percentuali, la nostra criptovaluta aumenta prima del 300% e poi del 500%, solo che il 300% è riferito al valore iniziale, 1, mentre il 500% al valore al momento del lancio sul mercato, cioè 1 aumentato del 300%, ossia 4. Se avessimo usato i moltiplicatori sarebbe stato tutto più chiaro: abbiamo prima un 4x e poi un 6x quindi in totale il moltiplicatore è 4*6= 24x, espresso in percentuale corrisponde ad un aumento del 2300% rispetto al valore iniziale.
Come si può intuire spesso le percentuali vengono usate per confondere le idee più che per chiarirle, l'esempio qui sopra mostra come a volte il fenomeno sia addirittura inconsapevole, però spesso è voluto e cercato. Per esempio se ieri la borsa è crollata del 50% e oggi invece è salita del 50% non è affatto vero che è tornata al valore dell'altroieri: sta sotto del 25%. Se invertiamo i termini e poniamo che ieri sia salita del 50% e oggi scesa del 50% invece risulta...la stessa cosa: è sempre sotto del 25% rispetto a due giorni fa!
Giocando un po' con situazioni di questo tipo si possono usare le percentuali per disorientare la gente, per esempio il debito pubblico viene sempre presentato come percentuale del PIL, in questo modo se il PIL aumenta del 2% e il debito pubblico dell'1% il governo può sbandierare ai TG che il debito pubblico è diminuito, quando invece in valore assoluto è aumentato.
[Nota a margine: sono ben consapevole che esistono dei motivi per i quali si usa molto più spesso il rapporto debito/PIL in luogo del valore assoluto del debito. Se stessimo parlando di un'azienda sarebbe normale considerare l'indebitamento in rapporto al fatturato perchè, prima di poter vendere qualsiasi cosa, è necessario produrla e pagare i relativi costi. Ma lo Stato non è un'azienda privata e debito pubblico e PIL non sono direttamente assimilabili a indebitamento e fatturato di un'attività privata.]
Morale della favola: diffidate sempre di una percentuale che non sia seguita da opportuno complemento di specificazione perchè nella migliore delle ipotesi è priva di senso, nella peggiore vi stanno prendendo per il culo.
FranZη
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
FranZη
Si prega Accesso a partecipare alla conversazione.
altrimenti mi troverò a parlare solo delle cose che sembrano interessanti a me.
Ciao FranZ,
a me onestamente piacciono questi tuoi "pensieri in libertà": ti leggo e mi godo sia gli argomenti che la scrittura, non vorrei inquinarli, per questo non intervengo.
Prosegui pure, l' assenza di commenti credo sia solo un non voler interrompere ... uhm, come dire ... l' artista all' opera, ecco

Ciao

You'll not see this coming.
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Questa volta sconfiniamo nel regno della Fisica, prendendo spunto da questo commento , dove in riferimento al rover lunare ci si chiede:
la questione è la differenza tra massa e peso. Domanda: perche' costruire un veicolo che deve resistere a 490 kg di PESO quando in realta' ne doveva sopportare 116?
In effetti la questione è proprio incentrata sulla differenza tra massa e peso. Quindi seguendo le buone abitudini per prima cosa definiamo queste due grandezze.
MASSA) Immaginiamo un corpo sospeso nel vuoto inizialmente non soggetto a nessuna forza. Se gli applichiamo una certa forza, il corpo comincerà ad accelerare finchè l'applicazione non cessa, a quel punto il corpo si troverà a muoversi di moto rettilineo uniforme. Se applichiamo una forza doppia, risulterà doppia anche l'accelerazione, in generale si trova sperimentalmente che forza e accelerazione, per ogni corpo, sono legate da una costante di proporzionalità. Questa costante si definisce massa inerziale e risulta legata alla forza e all'accelerazione dalla ben nota seconda legge di Newton: F=ma. Esiste anche un altro tipo di massa, la massa gravitazionale, ma prima che qualcuno possa scoraggiarsi dico subito che risulta equivalente alla massa inerziale, con ciò possiamo parlare di massa tout court. La massa gravitazionale misura la capacità di attrazione gravitazionale fra due corpi secondo la legge (sempre di Newton) F=G*m1*m2/r2. In Fisica la massa si misura in kg.
PESO) Il peso è la forza di attrazione gravitazionale che subisce un corpo sulla superficie di un corpo massiccio. Sulla terra si ricava dalle due equazioni di Newton qui sopra che Fpeso=mg dove g è l'accelerazione di gravità terrestre, ossia g=G*(massa terra)/(raggio terra)2. Il peso si misura in kg*metri/secondi2, altrimenti detti Newton (N). Siccome tutte le nostre bilance sono sulla terra, il peso è comunemente misurato in kg peso, o kg e basta (purchè non si faccia confusione con la massa), e dato che 1kg peso=9.8 N, evidentemente questa unità di misura alternativa per la forza è stata scelta proprio in modo che sulla terra massa e peso coincidano.
Ora avviciniamoci al nostro problema iniziale: il peso varia a seconda del luogo in cui ci troviamo secondo il rapporto:
accelerazione di gravità xxxx
- - - - - - - - - - - - - - - - - - - - - - - - - =: k
accelerazione di gravità terra
quindi noto il peso sulla terra di un corpo (espresso in kg o N non fa differenza) per trovare il peso che lo stesso corpo avrebbe sul pianeta xxxx basta moltiplicare il peso terrestre per k. La massa invece è una grandezza che dipende solo dal corpo e non dal luogo in cui si trova (escludendo effetti relativistici, e noi li escludiamo, oh se li escludiamo...!!!). Sulla luna la nostra costante k è uguale circa a un sesto.
Veniamo ora ad un esempio pratico. Sappiamo tutti quanto sia faticoso spingere un'automobile, soprattutto la prima spinta, quella da fermo. Questo perchè dobbiamo vincere l'inerzia dell'auto, legata alla sua massa. Trascurando gli attriti, se l'auto pesa 1000 kg, per imprimere un'accelerazione unitaria (1m/s2) dobbiamo darle una spinta di 1000 N. A questo punto se continuiamo a spingere dobbiamo solo contrastare gli attriti e non più l'inerzia, e infatti risulta molto meno faticoso spingere quando l'auto si muove.
Spostiamoci sulla luna. Come è evidente il peso lunare della nostra auto di prima sarà 1000/6=167 kg, quindi se siamo in tre o quattro potremmo anche pensare di sollevarla, ma se ci mettiamo a spingerla facciamo la stessa fatica che facevamo sulla terra, sempre al netto degli attriti (gli attriti in effetti dipendono anche dal peso, ma sono comunque trascurabili rispetto all'inerzia dell'auto). Quindi se volessimo andare in giro sulla luna motore e freni dovrebbero essere sostanzialmente gli stessi che permettono di condurre il veicolo sulla terra. Dal punto di vista della dinamica beninteso, cioè non considerando le ovvie problematiche relative all'ambiente estremo. E se -Dio ce ne scampi- dovessimo essere investiti dall'auto sulla luna riporteremmo le stesse conseguenze che avremmo sulla terra, perchè anche se la macchina pesa solo 167 kg è la sua massa di 1000 kg che ci viene addosso con la relativa energia cinetica di 1/2*m*v^2 -cioè la stessa che avrebbe sulla terra a parità di velocità v- e che le nostre povere ossa si troverebbero a fronteggiare. Sulla luna molto meglio essere messi sotto che centrati in pieno.
A questo punto dovrebbe sembrare abbastanza plausibile che pure le sospensioni e il telaio dovrebbero essere sostanzialmente dimensionate come sulla terra. Infatti se durante la marcia le ruote incontrano un ostacolo, un dosso per esempio, questo imprimerà un'accelerazione alle ruote che a loro volta la trasmetteranno al resto del veicolo, ciò comporterà una forza F=ma e anche in questo caso non compare il peso ma la massa inerziale, sempre quella, e sempre la stessa che si avrebbe in ambiente terrestre. Se assumiamo che le ruote non si stacchino dal suolo (le sospensioni servono per quello) questa accelerazione dipende principalmente dalla forma del dosso e dalla velocità del veicolo, e solo in misura ristretta dalla gravità lunare, quindi in sostanza la resistenza strutturale del mezzo deve essere paragonabile a quella terrestre, se vogliamo essere certi di evitare rotture, con gli evidenti problemi nel trovare un meccanico sulla luna.
Detto questo è poi evidente che la messa a punto per un veicolo lunare o terrestre non sarà la stessa, la rigidità delle molle e l'assorbimento degli ammortizzatori saranno sicuramente diversi, queste sono tra l'altro legate alla conformazione del suolo e alla velocità media di crociera del mezzo, anche per evitare effetti di risonanza: se percorrete una strada sterrata gli scossoni che sentite nell'abitacolo dipendono dalla velocità in modo assai complicato, può darsi che ad una data velocità veniate sbalzati da ogni parte mentre accelerando un poco vi trovate a sentire pochissimo le buche. Ma il punto fondamentale è che il mezzo deve avere una resistenza strutturale in grado di sopportare la sua massa e non solo il suo peso: sulla luna si è più leggeri, non più magri.
FranZη
Si prega Accesso a partecipare alla conversazione.
l'energia cinetica di cui parli è relativa a un veicolo in movimento orizzontale e quindi la forza viene dai motori, l'energia cinetica delle buche e' influenzata (anche) dalla velocita' verticale, che è influenzata dalla gravita' lunare, quindi minore.
quindi se lo scopo dell'auto lunare non è quello di raggiungere velocita' orizzontali elevate, la progettazione poteva essere orientata all'ottimizzazione di "peso"
per quanto riguarda le forze, in movimento si dovrebbe parlare piu' di MOMENTO, cioe' di risultante tra le varie forze in gioco, e nuovamente , dato chealcune componenti del momento sono calcolate come prodotto massa per velocita' ecco che nuovamente entra in gioco la gravita' lunare (la componente verticale della velocita' è data da accelerazione x tempo)
anche per gli attriti entra in gioco la componente verticale del peso, una auto di 1000 kg fluttuante nell'aria la posso spostare con niente....)
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
???gnaffetto ha scritto:
per quanto riguarda le forze, in movimento si dovrebbe parlare piu' di MOMENTO, cioe' di risultante tra le varie forze in gioco
Il momento è legato alla "leva" di una forza o di un insieme di forze, non è la loro composizione vettoriale (che è quella che si vede nel disegnino con l'ambulanza), ma in fondo cosa ci interessa a noi del momento?
Il prodotto massa x velocità è la quantità di moto del sistema, anche qui il momento non c'entra. In Fisica è necessario essere precisi. L'auto che fluttua nell'aria non la puoi spostare come niente perchè l'inerzia è la stessa che ha quando è appoggiata a terra, come dicevo sopra servono 1000 N per farla accelerare a 1 m/s2. Prova a spingere un grosso peso sospeso ad un paranco! Che gli attriti siano trascurabili rispetto all'inerzia lo dimostra l'esempio dell'auto: una volta in movimento si fa molta meno fatica a spingere, e quella fatica residua serve per contrastare gli attriti che evidentemente sono molto meno intensi dell'inerzia. Se l'auto fluttuasse senza alcun attrito data la prima spinta di 1000 N proseguirebbe a muoversi di moto rettilineo uniforme senza ulteriori spinte.e nuovamente , dato che alcune componenti del momento sono calcolate come prodotto massa per velocita' ecco che nuovamente entra in gioco la gravita' lunare (la componente verticale della velocita' è data da accelerazione x tempo)
anche per gli attriti entra in gioco la componente verticale del peso, una auto di 1000 kg fluttuante nell'aria la posso spostare con niente....)
Per quanto riguarda il disegnino, quella è una schematizzazione che si riferisce a tutt'altro: nel sistema di riferimento solidale all'ambulanza quando incontro uno "scollinamento" la forza peso risulta ridotta, c'entra molto poco con il nostro discorso. Peraltro la spiegazione fornita è una semplificazione grossolana, ed è in effetti scorretta dal punto di vista fisico: quella che viene chiamata "forza d'inerzia" evidentemente non è una forza, essendo definita come una "traiettoria". Nella situazione che ci interessa le cose si dovrebbero impostare più o meno così:
La curva blu rappresenta la traiettoria del centro di massa del veicolo. Raggiunto il dosso l'accelerazione "a" subita dal centro di massa dipende dalla velocità con cui viene preso il dosso e dalla sua forma, e solo in misura marginale dal peso dell'intero veicolo: è evidente che andando più veloci, o modificando la forma del dosso, la curva blu non sarà più la stessa, e dato che il peso non è variato sono necessariamente le altre due variabili a condizionare la curva.
Nota l'equazione della curva blu (e questa è la parte quasi impossibile da calcolare), ricavare l'accelerazione a=a(t) istante per istante è un giochetto: se chiamiamo la curva c=c(t) si ha:
c(t)=(x(t),y(t))
a(t)=d2 c(t)/dt2=(d2x/dt2,d2y/dt2)
Non c'è assolutamente niente in queste equazioni che stabilisca che la componente verticale dell'accelerazione (d2y/dt2) sia costante e uguale all'accelerazione di gravità, perchè in effetti non è vero: la componente verticale dell'accelerazione dipende dalla curva percorsa dal centro di massa.
FranZη
Si prega Accesso a partecipare alla conversazione.
l'esempio del peso sospeso non c'entra, la' si che si parla di momento angolare perche' c'e' un vincolo.
immagina invece l'auto sospesa nello spazio a velocita' 0 (inerzia 0) e di usare un piccolissimo razzo.. la sposterai.
i 1000N che tu calcoli sono riferiti alla forza necessaria per spostare di 1 metro al secondo (mi sembra) quella massa e.. continuare ad accelerare.... ma se io la muovo ad 1 centimetro al secondo i newton che mi servono sono 10... ( e non mi ricordo se era al quadrato.. quindi ancora meno se cambio il tempo)
ho capito che non mi sei di grande aiuto....
nel disegno l'inerzia è definito come vettore, cioe' un grandezza che contiene intensita', direzione e verso... io per semplicita' considero l'inerzia come l'energia immagazzinata dalla massa, e da ferma ogni massa ha inerzia zero.
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Io ho fatto quello che potevo per cercare di farti capire, a questo punto potrebbe esserti d'aiuto aprire un vero libro di fisica e studiarlo perché è abbastanza evidente che ne non lo hai mai fatto: prova a rileggere quello che hai scritto, non ha nessun senso. Oppure se hai come dici amici fisici chiedi lumi a loro, io gli argomenti che ho esposto li ho studiati alla facoltà di Fisica e se permetti so di cosa sto parlando.gnaffetto ha scritto: ho capito che non mi sei di grande aiuto....
FranZη
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Purtroppo però se mi fossi accorto all'inizio che il fatidico termine "gamma" compariva in entrambi i membri già nel post di kamiokande (invece mi era sfuggita la gamma a primo membro), avrei risparmiato altro prezioso tempo perchè le equazioni non presentano assolutamente nessun problema: se A=B allora kA=kB qualunque sia la costante k. Questo a livello matematico, in Fisica a rigore bisognerebbe aggiungere la postilla che k deve essere una grandezza adimensionale, perchè altrimenti risulterebbero variate le dimensioni fisiche dell'equazione, ma è proprio il nostro caso: gamma è il fattore di Lorentz ed è immediato verificare che si tratta di una quantità adimensionale.
Detto ciò ecco di seguito il calcolo, solo un'ultima nota: ovviamente l'unico interessato alla questione è, se lo è, kamiokande, però se qualcuno passa di qui per sbaglio può comunque verificare come si tratti di un piccolo miracolo il fatto che tutto questo casino dia alla fine per risultato...0!!! Avete presente quando a scuola vi davano quelle espressioni lunghe un chilometro e poi il riquadrino dava come risultato dell'esercizio 0? Ecco, una roba del genere.
EDIT: Mi sono accorto adesso che ho dimenticato gli accenti nel riquadro centrale: il termine a sinistra del primo "=" è (nabla)' x E', con gli accenti, cioè così come compare nell'ultimo riquadro (nabla è il simbolo "delta" rovesciato).
FranZη
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Altro esempio pratico: la famosa seconda legge di Newton F=ma è in realtà un'equazione vettoriale, scritta per esteso sarebbe:
cambierebbero in un qualche modo le caratteristiche della fisica di Newton? Ma neanche per idea, le due forme sono del tutto equivalenti, ovviamente si sceglie la forma senza coefficienti inutili aggiuntivi, ecco perchè nel calcolo del post precedente ho considerato il termine gamma finale del tutto ininfluente: se voglio divido ambo i membri per gamma e quello scompare, oppure moltiplico entrambi i membri dell'equazione vettoriale per la matrice:
FranZη
Si prega Accesso a partecipare alla conversazione.
- kamiokande
-

- Offline
- Utente
-

- Messaggi: 540
- Ringraziamenti ricevuti 188
La versione definitiva di invarianza è quindi questa scritta al post #51
Quando invece hai scritto al post #391) Un vettore è per definizione una n-pla di coordinate (lasciamo stare l'aggettivo "cartesiane" perchè oltre ad essere tecnicamente scorretto è fuorviante: porta a pensare subito ad uno spazio euclideo mentre la geometria differenziale -quella che stiamo affrontando qui- tratta spazi di qualunque tipo, purchè differenziabili), quindi la definizione di invarianza di un vettore è precisamente la definizione di invarianza coordinata per coordinata. Questa è geometria e vale indipendentemente dalla validità o meno della relatività
e questo al post #41Per quanto non sia sicuro di quello che intendevi scrivere con le tue equazioni, dato che mancano i passaggi, comunque mi pare di aver capito che si trascuri che il termine gamma sia proprio la contrazione della componente "x", ergo le due equazioni hanno la stessa forma, ed è proprio quello che si intende per "invarianza".
Perché, se non avevi visto che gamma compariva in ambo i membri, invece di scrivere che sicuramente avevo sbagliato, visto che gamma deve essere almeno in ambo i membri, hai scritto invece:Non ha senso proseguire questa discussione qui, ti faccio solo notare che le equazioni sono esattamente le stesse se usi il nuovo sistema di riferimento, se usi il vecchio (cosa che hai fatto sopra) ovviamente no. Questo è il significato di trasformazioni in generale su una qualunque varietà riemanniana, se non ti sta bene, devi buttare via non solo la relatività ma tutta la geometria dal 1800 in poi. Ovvio che la densità di carica, essendo una funzione delle coordinate, nel nuovo sistema di riferimento va considerata rispetto alle nuove coordinate spazio-temporali, infatti nelle equazioni qui sopra usa rho_0 in luogo di rho, ma non se ne è mica accorto lui: cambiare il sistema di coordinate vuol dire cambiarle tutte, non solo quelle che ci fanno comodo.
si trascura che il termine gamma sia proprio la contrazione della componente "x", ergo le due equazioni hanno la stessa forma, ed è proprio quello che si intende per "invarianza" ?
Quando poi ti spingi oltre dicendo al post #51
Mi pare di capire che questo fatto che un fattore adimensionale "non modifica sostanzialmente un'equazione", ovvero che il significato fisico di un'equazione "rimane del tutto equivalente" se ne moltiplico un membro per una quantità adimensionale, è una proprietà generale e non si applica solo alle equazioni di Maxwell? O ho capito male?2) La versione "corretta" delle equazioni di Maxwell è quella che trovi in qualunque testo di Fisica, o anche su wikipedia, con rho al posto del secondo membro della prima equazione qui sopra, che d'altronde è del tutto equivalente essendo la quantità tra parentesi una quantità adimensionale, come ho già provato a più riprese di spiegare. E' solo un cambiamento di unità di misura che non modifica la sostanza dell'equazione, così come darti una spinta di 9.8 Newton o di 1 kg_f significa dare esattamente la stessa spinta.
"La stampa è morta" (Egon Spengler - Ghostbuster)
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Ho già spiegato che non avevo visto all'inizio la gamma a primo membro delle tue equazioni, e questo è il motivo per cui ho fatto a mano il conto, ma incidentalmente il mio conto conferma quello che avevo sostenuto al post #39 che mi contesti qui sopra: la gamma compare fra le vecchie e le nuove equazioni, non all'interno delle nuove come avevi sostenuto nel tuo commento originale (cosa che d'altronde, come spiegato nell'ulteriore post , non cambierebbe di una virgola il discorso). Infatti all'inizio, quando mi sfuggiva ancora la prima gamma, pensavo già che l'errore dovesse essere di questo tipo: confrontare il vecchio e il nuovo sistema di riferimento. Qui sopra compare un calcolo che puoi:
a) contestare allegando il/i passaggi sbagliati;
b) confermare e con esso anche l'invarianza dell'equazione di Maxwell in questione.
La matematica funziona così: tertium non datur (salvo logica intuizionista che però non ci interessa qui).
Per concludere, sottolineando che non mi riferivo a te quando parlavo di "scuole medie" ma al fatto che si tratta di un'uguaglianza algebrica arcinota, per quanto riguarda la "versione corretta delle equazioni di Maxwell" devo dirti che nella discussione originale pensavo, almeno all'inizio, di essere ad un altro livello di discussione, francamente la variante che hai postato dell'equazione di Maxwell non è affatto una versione relativistica, è semplicemente la versione originale dove la nuova densità di carica viene sostituita dalla vecchia non accentata, quella nel sistema di riferimento fisso: dato che rho è una carica diviso un volume, se la coordinata "x" viene contratta di un fattore gamma allora rho' risulterà moltiplicata per questo fattore. Però scusa ma qui siamo a un livello veramente elementare della questione, non si può pensare di contestare la relatività su queste basi.
Da ultimo vorrei puntualizzare che non sono un fanatico della relatività, credo che sia solo una bella teoria astratta così come lo fu prima di lei la gravità di Newton, e credo altresì che siamo lontanissimi dal capire la natura ultima della gravità o di qualunque altra profonda verità della Fisica. Infine ti ringrazio per l'opportunità che mi hai dato di approfondire concetti che davo per scontati (la Lorentz-invarianza delle equazioni di Maxwell), fare il calcolo con le proprie mani, oltre ad essere un utile ripasso, è una prova superiore a mille capitoli di libri di Fisica.
Edit: stavo lasciando senza risposta quest'ultimo dubbio:
Non hai capito proprio. Ho ripetuto allo sfinimento che stai moltiplicando entrambi i membri di una equazione per la stessa quantità adimensionale, nel nostro caso gamma. L'hai scritto tu stesso postando le tue equazioni, non realizzo proprio come tu possa avere ancora dubbi in merito.Mi pare di capire che questo fatto che un fattore adimensionale "non modifica sostanzialmente un'equazione", ovvero che il significato fisico di un'equazione "rimane del tutto equivalente" se ne moltiplico un membro per una quantità adimensionale, è una proprietà generale e non si applica solo alle equazioni di Maxwell? O ho capito male?
FranZη
Si prega Accesso a partecipare alla conversazione.
- kamiokande
-

- Offline
- Utente
-

- Messaggi: 540
- Ringraziamenti ricevuti 188
Da quel che hai scritto sia qui che nel post post di Marconi, io ho capito che rispetto alla matrice da te introdotta:
dove k è un parametro adimensionale a scelta (uso k e non gamma onde evitare confusione), la seconda legge di Newton è invariante.
Domanda: Questa mia interpretazione è corretta? (Mi basta un sì o un no).
Secondo punto, alla mia domanda riguardo su quale fosse la versione corretta della prima equazione di Maxwell tra queste due:
a)
b)
tu hai risposto così:
Nel quale mi spieghi in maniera molto chiara, a mio parere, che le due equazioni sono "tutto equivalenti essendo la quantità tra parentesi una quantità adimensionale."2) La versione "corretta" delle equazioni di Maxwell è quella che trovi in qualunque testo di Fisica, o anche su wikipedia, con rho al posto del secondo membro della prima equazione qui sopra, che d'altronde è del tutto equivalente essendo la quantità tra parentesi una quantità adimensionale, come ho già provato a più riprese di spiegare. E' solo un cambiamento di unità di misura che non modifica la sostanza dell'equazione, così come darti una spinta di 9.8 Newton o di 1 kg_f significa dare esattamente la stessa spinta.
Domanda: Questa affermazione vale solo per questa equazione o è del tutto generale?
Non cerco di metterti in difficoltà, ho solo difficoltà a capire le tue affermazioni e voglio essere sicuro di non interpretarle male onde evitare discussioni inutili.
P.S: Rispetto la mia uscita sulle scuole medie la mia era solo una battuta, non me la sono presa. Non andiamo più sul personale, ammetto che a volte mi faccio trascinare troppo anche se non dovrei. Rimaniamo sul pezzo.
"La stampa è morta" (Egon Spengler - Ghostbuster)
Si prega Accesso a partecipare alla conversazione.
- kamiokande
-

- Offline
- Utente
-

- Messaggi: 540
- Ringraziamenti ricevuti 188
"La stampa è morta" (Egon Spengler - Ghostbuster)
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Sì.Domanda: Questa mia interpretazione è corretta?
2)
E' del tutto generale.Domanda: Questa affermazione vale solo per questa equazione o è del tutto generale?
********************************************************************************************
Ora se posso fare un breve commento aggiuntivo, per quanto riguarda la 1) non capisco come si possa considerare un vettore come diverso dalla tripla di coordinate che lo definisce. Forse perchè stai pensando alla notazione della somma vettoriale, per intenderci quella del tipo:
Attenzione però, si intende:
Per quanto riguarda la domanda 2) ti ho già segnalato che quella stessa scrittura che riguarda rho si trova nell'articolo di Lorentz del 1904, per la precisione è la formula (7), quindi si tratta di un fatto già noto prima che venisse concepita la relatività ristretta. E si tratta, come specificato sopra, di un cambiamento di unità di misura, in generale, e di un cambiamento di sistema di riferimento (che comporta anche il cambiamento nell'unità di misura dovuto alla contrazione di Lorentz), nel caso specifico: nella formula a) la densità è quella del riferimento del sistema, nella b) la densità è quella in un sistema di riferimento considerato "fisso".
FranZη
Si prega Accesso a partecipare alla conversazione.
- kamiokande
-

- Offline
- Utente
-

- Messaggi: 540
- Ringraziamenti ricevuti 188
Prendiamo un sistema di riferimento inerziale S rispetto al quale un corpo di massa costante m accelera uniformemente per esempio con la seguente accelerazione:
Prediamo ora il sistema di riferimento S' trasformato con la matrice T dove k è una costante qualunque, rispetto a questo sistema di riferimento il corpo accelera invece con la seguente accelerazione:
da cui si osserva immediatamente che le due accelerazioni sono diverse sia in modulo che in direzione, e quindi per i due osservatori il corpo accelera diversamente sotto l'effetto di due forze diverse:
di conseguenza la seconda legge di Newton NON È INVARIATE rispetto alla trasformazione T. Vediamo ora come si esplicita correttamente l'invarianza rispetto alla trasformazione di Galileo. Prediamo un terzo sistema di riferimento S'' che trasla rispetto ad S con una velocità costante v, e di conseguenza è anch'esso inerziale. Rispetto a S'' la velocità del corpo u, misurata rispetto a S, si scrive in generale come:
differenziando nel tempo ambo i membri otteniamo l'accelerazione e di conseguenza la forza che agisce sul corpo:
Quindi sia per S che per S'' il corpo accelera con la stessa accelerazione sotto l'effetto della stessa forza. Questo è quello che si intende in fisica per invarianza.
Veniamo ora al secondo punto. Prendiamo la quantità di moto relativistica così definita:
che differisce dalla versione classica di Newton per il solo fattore di Lorentz
che secondo quel che dici è un semplice cambio di unità di misura. In realtà i due comportamenti sono molto diversi:
| Quantità di moto | Legge oraria |
La legge oraria di un corpo di massa costante, e soggetto ad una forza F costante, secondo la meccanica relativistica è un iperbole, mentre secondo la meccanica Newtoniana è una parabola. La seconda legge di Newton scritta in forma relativistica diventa:
Quindi la seconda legge di Newton non è invariante rispetto alle trasformazioni di Lorentz. Se sei interessato posso anche scriverti come cambiano le equazioni di Maxwell se si accetta di contrarre anche la densità di carica come suggerito da Jefimenko.
In conclusione, affermare che le trasformazioni di Lorentz sono solo un cambio di unità di misura, o che la sostanza della fisica non cambia, significa implicare che la teoria di Einstein ha avuto un impatto nullo sulla fisica del 1900.
"La stampa è morta" (Egon Spengler - Ghostbuster)
Si prega Accesso a partecipare alla conversazione.
- Messaggi: 850
- Ringraziamenti ricevuti 118
Attenzione però, si intende:
F=ma <---->T*F=T*ma
e non:
F=ma <---->F=T*ma
che ricade invece nel punto 2). , quello dei cambiamenti di unità di misura.
Ora se vogliamo fare davvero un passo avanti vediamo di chiarire al di là di ogni dubbio di cosa si parla.
1) Il primo punto da te sollevato riguarda questa equazione che hai postato:
Se vogliamo usare sempre la legge di Newton come prototipo di equazione, e la matrice T da te introdotta sopra come trasformazione, rientriamo in questa tipologia di equivalenza:
Questa ovviamente non è una trasformazione del sistema di coordinate da cui dipendono i vettori "F" e "ma", ma una trasformazione algebrica dello spazio vettoriale in cui "vivono" questi vettori. Senza giri di parole stiamo trasformando i vettori che indichi con i, j, k in T*i, T*j, T*k e non il tensore xi in x'i. Si tratta quindi di una equivalenza algebrica che vale qualunque sia il significato che diamo a "F" e a "ma" che ci dice che se il vettore "F" è uguale al vettore "ma" in una data base, allora continua ad essere uguale in qualunque altra base dello spazio vettoriale.
2) Il secondo punto nasce invece dall'equazione:
che ci porta a questo tipo di equivalenza:
3) Veniamo ora all'invarianza di un'equazione rispetto a un gruppo di trasformazioni del sistema di riferimento, che come hai giustamente sottolineato è la vera invarianza delle leggi della Fisica. In questo caso il prototipo dell'equivalenza è:
Nel riquadro 3 compaiono le trasformazioni delle coordinate con relativa matrice, poi dopo i passaggi intermedi nel riquadro 7 c'è la versione accentata dell'equazione di Maxwell in questione, che quindi risulta invariante rispetto alla trasformazione di Lorentz. A questo proposito ti pongo anche io una domanda alla quale basta un sì o un no come risposta:
Domanda: i passaggi del calcolo sono corretti?
Va da sè che se la risposta è sì allora devi ammettere la Lorentz-invarianza, se la risposta è no gradirei che segnalassi dove sta l'errore. Penso che più chiaro di così non riuscirò ad essere quindi spero che questa volta possiamo riuscire a parlare la stessa lingua. C'è ancora un'altra cosa da aggiungere però:
Come spero di aver chiarito qui sopra non ho mai affermato quello che mi fai dire qui, inoltre ti ho già segnalato che la "contrazione di Jefimenko" è già presente esplicitamente in Lorentz ancora prima che Einstein e poi Minkowski dessero alla relatività ristretta la forma che ha adesso, ragion per cui è universalmente nota come "contrazione di Lorentz". Come altresì non ho mai detto che le trasformazioni di Lorentz sono solo un cambio di unità di misura, ho detto che se le fai a metà come nell'equazione da te postata e trattata nel punto (2) quello che salta fuori è un cambio di unità di misura.Quindi la seconda legge di Newton non è invariante rispetto alle trasformazioni di Lorentz. Se sei interessato posso anche scriverti come cambiano le equazioni di Maxwell se si accetta di contrarre anche la densità di carica come suggerito da Jefimenko.
In conclusione, affermare che le trasformazioni di Lorentz sono solo un cambio di unità di misura, o che la sostanza della fisica non cambia, significa implicare che la teoria di Einstein ha avuto un impatto nullo sulla fisica del 1900.
FranZη
Si prega Accesso a partecipare alla conversazione.
- kamiokande
-

- Offline
- Utente
-

- Messaggi: 540
- Ringraziamenti ricevuti 188
Nel caso in questione, rispetto alla matrice T, non c'è differenza tra F' = T*F ed F' = T*m*a perché l'equazione di Newton vale per S' come per S, quindi anche scrivendo
dove nonostante la forma della legge di Newton per S' è esattamente la stessa che per S, e che le componenti cartesiane siano (ovviamente) "invarianti", non cambia il fatto che
I due osservatori, S' ed S, osservano perciò due fenomeni diversi e, in questo caso, non si possono riconciliare se non introducendo un ulteriore termine di accelerazione (visto che non basta solo moltiplicare tutto per un fattore di scala)
quindi la seconda legge di Newton non è invariante rispetto a T malgrado siano "invarianti" le componenti cartesiane. Il punto per me è tutto qui: se la per legge di Newton l'invarianza delle componenti cartesiane non è sufficiente a garantirne l'invarianza in senso fisico, perché dovrebbe esserlo per le equazioni di Maxwell?
Venendo alla tua domanda, i tuoi passaggi sono corretti?
La mia risposta è: non ha importanza, visto che il tuo risultato è lo stesso che avevo già scritto io.
Quindi, l'equazione è invariante rispetto alle trasformazioni di Lorentz?
La mia risposta è no. Perché? Perché l'osservatore S osserva/misura un fenomeno diverso da S'. Il fatto che le due componenti ( (rotE)x e dBx/dt ) si eguagliano per entrambi i sistemi di riferimento, e che rimangono uguali anche moltiplicandole entrambe per lo stesso numero, ti assicuro che mi è sempre stato chiaro ed il tuo ripeterlo non gioverà alla discussione. Anche in questo caso, per riconciliare l'osservazione fatta da S' con l'osservazione fatta da S dello stesso fenomeno, occorre sommare all'equazione scritta da S' un ulteriore termine vettoriale (o banalmente moltiplicare ambo i membri per T^⁻1), cosa che ne implica la non invarianza.
È interessante notare che lo stesso Einstein, nel suo lavoro "on the electrodynamics of moving bodies", afferma che tutte le componenti della forma originale delle equazioni di Maxwell differiscono della forma trasformata (con Lorentz) per una funzione psi(v), ma siccome le due forme devono essere identiche allora tale funzione deve essere per forza uguale ad 1. Questo fatto non è direttamente collegato a quanto sto cercando di spiegare, ma fa capire come spesso le pretese "dimostrazioni" si fondino sulle delle basi dalla dubbia solidità.
Assolutamente no! Sono due cose diverse. La domanda che fa Jefimenko è chiarissima: se una barra (o una scala come nel noto paradosso della scala e del fienile) in moto rispetto al sistema S (S' qui non centra nulla) si contrae secondo Lorentz, perché non dovrebbe farlo un corpo carico elettricamente?inoltre ti ho già segnalato che la "contrazione di Jefimenko" è già presente esplicitamente in Lorentz ancora prima che Einstein e poi Minkowski dessero alla relatività ristretta la forma che ha adesso, ragion per cui è universalmente nota come "contrazione di Lorentz".
Nella trattazione che si trova in letteratura la trasformazione della densità di carica è questa:
per cui rho (rho') è considerato sempre a riposo rispetto a S (S'), oppure invariante per definizione (non è chiaro). Jefimenko si è posto la domanda di cosa accade nel caso generale che un corpo carico elettricamente sia in movimento rispetto a S e/o S', per cui:
Questo fatto non è presente esplicitamente nelle equazioni di Maxwell, perché banalmente non lo può essere visto che per Maxwell un corpo in movimento non si contraeva come per Lorentz. Per intenderci, il fattore di Lorentz in questione non è dovuto a gamma, quindi alla trasformazione tra due osservatori S ed S', ma è riferito alla velocità u del corpo, e non alla velocità v di un generico sistema S'.
Riguardo al tuo insistere sull'equivalenza rispetto ad un cambio di unità di misura, come ho mostrato, moltiplicando il fattore adimensionale di Lorentz alla quantità di moto si cambia il senso fisico della seconda legge di Newton, poiché viene introdotto un secondo termine di accelerazione, ed allo stesso modo nella soluzione generale delle equazioni originali Maxwell (vedi per esempio a pag. 247 del libro di John David Jackson "Classical Electrodynamics" terza edizione )
contraendo le densità elettrostatiche secondo Lorentz, si ottiene questo
appaiono cioè delle velocità assenti nella forma originale che, specialmente all'interno dei termini derivati nel tempo, ne alterano il senso fisico, e non si può paragonare questo impatto ad una mera variazione di unità di misura.
"La stampa è morta" (Egon Spengler - Ghostbuster)
Si prega Accesso a partecipare alla conversazione.