La formula del latte è Vacca2O

Shavo ha scritto: Capisco che non capisco. Non ho le basi per tradurre il tuo linguaggio.

Eh, allora è colpa mia perchè nelle mie intenzioni dovrei farmi capire anche da chi non ha alle spalle solidi studi matematici. Ci riprovo: le somme di infiniti numeri, che come già detto si chiamano serie, sono il pane quotidiano dell'analisi matematica, dato che ogni funzione analitica può essere scritta in forma di serie. Ne avevo già riportato un esempio qui sopra , quando parlavo della formula magica, in quel post compare la serie associata alla funzione esponenziale. La discriminante tecnica di cui parlavo sta qui: le serie si dividono in "assolutamente convergenti" e non. Assolutamente convergente significa che la serie non ha valore infinito anche se al posto dei termini originali consideriamo il valore assoluto di questi termini (da qui l'avverbio "assolutamente"). Per esempio la serie S=1-1+1-1+... di cui parlavo prima non è assolutamente convergente perchè se la riscriviamo con i valori assoluti dei termini diventa 1+1+1+1+... che diverge a infinito (il valore assoluto è il numero senza segno, cioè è lo stesso numero se questo è positivo, oppure il numero senza meno se è negativo, per cui +1 resta 1 e -1 diventa 1).

Ora la differenza fra i due tipi di serie, assolutamente convergenti e non, è che le prime possono essere trattate come delle somme finite, quindi scambiando l'ordine dei termini non cambia il valore della serie, le seconde invece no, anzi, come già visto a seconda di come rimescoliamo i termini possiamo farle convergere a qualunque numero. Ecco allora che anche volendo dare un senso preciso alla "somma di tutti i numeri" (cosa che si potrebbe anche fare), questa somma infinita sarebbe giocoforza non-assolutamente-convergente e quindi il suo valore dipenderebbe dall'ordine particolare in cui scriviamo i termini.

Visto che la somma 1+1+1+1... l'avevo già buttata lì, e adesso è ritornata, spiego un momento la storia delle due serie dell'aneddoto di Hardy-Ramanujan. Ovviamente 1+1+1+... fa infinito, e lo stesso dicasi di 1+2+3+..., perciò le due scritture:

1+1+1+...=-1/2 ....................... (1)
1+2+3+...=-1/12 .....................

sono due bestialità, prese così alla lettera. In realtà hanno ragione di esistere, e questa ragione è simile a quella che legava la somma 1-1+1-... alla funzione 1/(1+x) dell'aneddoto di Leibniz. In questo caso la funzione da considerare, come già detto, è la zeta di Riemann, così definita:

ζ(x)=Σ n^-x ................. (2)

dove la sommatoria Σ è estesa a tutti gli interi positivi 1,2,3,... (un'altra funzione definita tramite una somma infinita...). Scrivendola per esteso i primi termini sarebbero:

ζ(x)=1+1/2^x+1/3^x+1/4^x+...

Si può in effetti dimostrare che ζ(0)=-1/2 e ζ(-1)=-1/12, perciò sostituendo questi particolari valori di x nella (2) otteniamo proprio le "uguaglianze" (1). Per non lasciare nulla all'immaginazione ecco come funziona con x=-1:

ζ(x)=1+1/2^-1+1/3^-1+1/4^-1+...=1+2+3+4+...

L'inghippo sta nel fatto che la funzione ζ può essere scritta nella forma (2) solo se x è maggiore di 1. Per tutti gli altri valori di x bisogna trovare altri modi di definire la funzione, nessuno dei quali conduce ai paradossi delle (1). Lo stesso valeva per la funzione 1/(1+x) della serie di Leibniz, questa definizione era valida solo se -1<x<1, dunque il valore x=1 che avevamo usato era al di fuori (per un pelo!) dal campo di definizione. Niente dimostrazione della creazione del mondo dal nulla quindi.

Carissimo, fossimo dal vivo potrei usare la mimica per risolvere il tutto con una risata.... MA se non hai bisogno di una spalla comica ti anticipo che con me ci son poche speranze..

per me è arabo.. (e non mi riferisco al sistema di numerazione)

@Shavo
Va bene prometto di non parlarti più delle serie :ok:

Quasi mi vergogno affacciarmi a tanta eccellenza, da bimbo, ridicolo, paradossalmente amavo e odiavo numeri primi, il 23 il 5 mi stavano sul cazzo, anzi..poi amavo indiscutibilmente il 13 il mio compleanno, l'11 e il 29..pure il 7 non "nuoce".
..poi il 2? È davvero numero primo?..ignorando lo ZERO piuttosto che virgola...
Mi sdogano citando un libro che ben comprendendo..mi rende "curioso": Il mistero dell'alef di AMIR D. ACZEL Qualcuno lo conosce?
..poi, potrei andare in VACCA...

OrtVonAllen ha scritto: poi amavo indiscutibilmente il 13 il mio compleanno, l'11 e il 29..pure il 7 non "nuoce".
..poi il 2? È davvero numero primo?

Pure io sono nato il 13, di un anno primo. La mia data di nascita si fattorizza in 227 e 577, potrebbe quindi essere usata come supporto per un messaggio tipo quello di Arecibo , un po' più corposo però...

Mi sdogano citando un libro che ben comprendendo..mi rende "curioso": Il mistero dell'alef di AMIR D. ACZEL Qualcuno lo conosce?

Non lo conosco, ma non ho molta simpatia per quel genere di esposizione. Poco tempo fa mi hanno regalato "Storia compatta dell'infinito" di David Foster Wallace, insomma...diciamo che preferisco leggermi Cantor in originale (vabbè, tradotto dal tedesco) piuttosto che le varie interpretazioni postume.

Per me i numeri sono stati d'animo, quelli primi poi...non so quantificare matematicamente il perché, ma ne sono certo.
Come sono certo che i numeri primi non raccontano una "vicenda" bidimensionale...è quello l'errore che depista certe "logiche"..ho da qualche parte, dei calcoli che ho fatto (istintivi) che togliendo il 2 e il cinque, la sequenza degli altri, diventava "armonica" fino a poco meno di 10000...
Era un calcolo che affrontava gli spazi "dilatati" senza nessun ragionamento di base..anzi una specie di moltiplicare sottrarre dividere ed aggiungere...ma rimaneva inspiegabilmente logico ripeto senza il due ed il 5...

I numeri sono magici, ma nel rapporto della relatività di una data, si fossero sbagliati di 31un ore? (ci vuole l'accento in questo caso? 31un'ore? anche qui matematica e "arte")...beh...non voglio andare in OT, ma fosse a cavallo con un segno zodiacale piuttosto a un destino numerologico...diventa relativo, gli ebrei "anno" un calendario, noi su una relativa nascita di Cristo..eccetera eccetera...infatti ciò rientra nel mistico numerico.
Ma poi abbiamo quello piatto, fatto di prove..e oggi sono approssimazioni. Se c'è poi lo zero e virgola..diventa il relativo 3,14 o 6,28 un metaforico cerchio che per chi è miope rimane un punto...nel microcosmo non lo so, mi affido a "d'io"..

www.repubblica.it/2009/04/sezioni/scienz...mo/numero-primo.html
www.panorama.it/cultura/libri/un-enigma-...-milione-di-dollari/

OrtVonAllen ha scritto: Per me i numeri sono stati d'animo, quelli primi poi...non so quantificare matematicamente il perché, ma ne sono certo.
Come sono certo che i numeri primi non raccontano una "vicenda" bidimensionale...è quello l'errore che depista certe "logiche"..ho da qualche parte, dei calcoli che ho fatto (istintivi) che togliendo il 2 e il cinque, la sequenza degli altri, diventava "armonica" fino a poco meno di 10000...

Si può discutere se 1 sia o meno primo, nella definizione di numero primo tocca escluderlo esplicitamente altrimenti ci sarebbe dentro. Lo zero si esclude da sè. Sul 2 e il 5 pochi dubbi: senza di loro non esisterebbe nessun Teorema Fondamentale dell'Aritmetica e perciò dell'aritmetica stessa resterebbe ben poco. D'altronde i numeri primi sono decisamente "armonici" con il 2 e il 5, sono infatti legati da una famosa identità (dovuta a Eulero) con la funzione ζ di Riemann introdotta sopra:

ζ(x)=Π 1/(1-p^-x)

dove Π indica il prodotto da estendersi a tutti i numeri primi p (2 e 5 compresi). Siccome ζ(x) è una generalizzazione della serie armonica (anzi, per x=1 diventa proprio la seria armonica), non serve poi molto per trovare armonia anche nei numeri primi. Detto en passant Riemann usò la funzione zeta proprio per questioni legate ai numeri primi, fra le altre gli servì per trovare una formula esatta per la funzione enumerativa dei numeri primi , una roba che cercavano dai tempi di Euclide, mica cazzi insomma.

Questioni serie

Qualche tempo fa si è parlato di serie, ossia di somme infinite, con tanto di esempi tratti dall'analisi. L'idea di sommare infiniti numeri può sembrare piuttosto balzana, e sicuramente scollegata dalla realtà. O una sega mentale a pieno titolo, se preferite. Niente di più falso. Le serie in realtà ci toccano da vicino quotidianamente, dato che la matematica finanziaria ne fa largo uso, ragion per cui i risultati teorici sulle somme infinite influenzano il nostro conto corrente o i nostri finanziamenti.

Per introdurre il tema, iniziamo con qualcosa di soft, cioè con una somma finita. Questa:

(1) Σⁿ_k=0 x^k = 1+x+x²+...+xⁿ

Abbiamo già visto che questa somma, se prolungata all'infinito, diventa una serie nota come serie geometrica. La sua versione finita, quella qui sopra troncata all'esponente n, prende il nome tecnico di ridotta n-esima, per la cronaca. La somma (1) nella matematica finanziaria è di importanza capitale (non so se avete colto il divertentissimo gioco di parole...) per via della seguente formula:

(2) 1+x+x²+...+xⁿ = (1-xⁿ⁺¹)/(1-x) .................. per x diverso da 1

Prima di spiegare dove stia il collegamento tra formula e finanza vediamo un momento come si dimostra la (2), dato che mi sembra una questione che vale la pena di essere approfondita. Quando si ha a che fare con formule che coinvolgono i numeri naturali (0,1,2 eccetera), nel nostro caso gli esponenti della "x", un metodo di dimostrazione molto utilizzato è quello detto per induzione. Preciso subito che l'induzione matematica non ha nulla a che fare con quella filosofica, come potrete accertarvi fra un istante. Il procedimento si divide in due passi distinti:

I passo: si verifica che la formula è vera per n=0, sostituendo quindi 0 a n risulta:
1=(1-x)/(1-x)
che è banalmente verificata.

II passo: si dimostra che se la formula è vera per n, allora è vera anche per n+1. La prima parte della condizionale è detta ipotesi induttiva. Nel nostro caso:
1+x+x²+...+xⁿ⁺¹=(1-xⁿ⁺¹)/(1-x)+xⁿ⁺¹=(1-xⁿ⁺²)/(1-x)
L'espressione che sta in mezzo è ottenuta applicando l'ipotesi induttiva, cioè considerando vera la formula per il numero naturale n, mentre l'ultima a destra è la nostra formula con n+2 al posto di n+1, che è proprio quello che dovevamo ottenere dato che anche la somma iniziale aveva l'esponente aumentato di 1 (in altri termini è la formula (2) con n+1 al posto di n). Come volevasi dimostrare.

Dovrebbe essere chiaro come funziona l'induzione matematica: se una formula è vera per n=0, e ogni volta che è vera per un numero n è vera anche per il suo successore n+1, allora la formula è vera per tutti i numeri naturali. Avrete notato che il procedimento è molto semplice e non richiede certo fantasia, a fronte di queste virtù ha però una grave pecca: bisogna già conoscere la formula giusta. L'induzione matematica senza la formula corretta comporterebbe solo una vana ricerca fra le possibili candidate, che sono in numero infinito.

Ecco allora che, questa volta usando un po' di fantasia (e di algebra), possiamo anche trovare un metodo di dimostrazione costruttivo. Iniziamo a definire:

S_n:=1+x+x²+...+xⁿ
S_n+1:=1+x+x²+...+xⁿ⁺¹

I due punti davanti all'= sono una notazione standard che indica che trattasi di uguaglianza per definizione. Risulta abbastanza evidente (fate la prova!) che valgono queste due uguaglianze per la somma troncata all'esponente n+1:

S_n+1 = S_n+xⁿ⁺¹
S_n+1 = 1+x*S_n

dunque i due membri di destra sono uguali tra loro, e risolvendo rispetto a S_n la semplice equazione che ne deriva si ottiene:

S_n=(1-xⁿ⁺¹)/(1-x)

che è per l'appunto la nostra formula (2), già bella e dimostrata dato che l'abbiamo ricavata con passaggi algebrici. Veniamo ora al collegamento tra formula e matematica finanziaria. Tutto parte dal concetto di rendita. Diciamo che alla nascita di vostro figlio decidete di aprirgli un libretto di risparmio, sul quale ad ogni compleanno verserete una certa quota "R", fino al raggiungimento della maggiore età, quando il giovine avrà accesso all'intero capitale. Si spera per pagarsi gli studi e non la droga. La banca presso cui avete aperto il libretto vi garantisce un certo tasso d'interesse "i". Passati i 18 anni, quale sarà il montante (= il capitale accumulato comprensivo degli interessi)?

Si ragiona così: al primo anno versate la quota R che viene capitalizzata (= gli viene calcolato l'interesse) 17 volte, la rata versata al secondo anno è capitalizzata 16 volte, e così via fino all'ultima rata sulla quale non si applica interesse. Astraendo un poco la situazione, e indicando con "n" il numero degli anni in cui si percepisce la rendita, il montante "M" risulta essere:

M=R*(1+i)^n-1+R*(1+i)^n-2+...+R*(1+i)+R

Se raccogliamo la "R" che compare in ogni termine e chiamiamo x=1+i possiamo riscrivere l'uguaglianza così:

M=R*(1+x+...+x^n-2+x^n-1)

e la somma tra parentesi è proprio una ridotta (n-1)-esima della serie geometrica, alla quale possiamo applicare la formula (2), ottenendo:

M=R*(1-xⁿ)/(1-x)

e siccome avevamo posto x=1+i, risostituendo alla x il termine contenente l'interesse "i" abbiamo infine:

(3) M = R*( (1+i)ⁿ-1) /i

La formula (3) è valida solo se l'interesse è diverso da zero. Tornando alla rendita del pargolo, se per esempio versate 500 euro all'anno e la banca riconosce il 2% di interesse (coi tempi che corrono è grasso che cola), il montante sarà di 10700 euro e qualche spicciolo. Ora immagino qualche rimostranza da parte di chi legge, perchè la situazione della rendita appena esposta non è che sia così diffusa. A me per esempio non è capitato. Però invertendo questo concetto otteniamo quello, molto più diffuso, di pagamento rateizzato (mutuo, leasing, finanziamento, ecc.). Ragionando specularmente a quanto fatto sopra si ottiene quest'altra formula:

(4) A = R*( 1-(1+i)^-n) /i

dove "A" sta per l'importo finanziato, "R" è la rata, mentre "i" e "n" hanno lo stesso significato di prima. Spesso la formula (4) si usa per ricavare la rata "R" noti l'importo da finanziare "A", l'interesse e la durata del finanziamento. Sempre a titolo d’esempio, con gli stessi valori usati sopra per rata, interesse e numero di anni, l’importo finanziato “A” risulta essere di 7496 euro.

Finora abbiamo incontrato solo somme finite, quindi non è stata ancora giustificata l'affermazione iniziale che parlava di somme infinite legate a questioni finanziarie. Ma ormai ci siamo, perchè le serie nella finanza compaiono contestualmente ai prestiti delle banche, e adesso vediamo come. Come è noto la banca è tenuta ad avere sempre a disposizione una certa parte dei depositi dei correntisti, per ovvie ragioni. Questa frazione è stabilita dalla riserva frazionaria, che altro non è che la percentuale di denaro effettivamente a disposizione dei correntisti. Detto in altri termini, se andassimo tutti insieme a prelevare tutti i soldi sul conto, è quello che troveremmo effettivamente. Attualmente la riserva frazionaria è all'1%. La banca dunque conserva in cassa questa quota "r" e usa per prestiti, mutui, finanziamenti la restante quota 1-r (ogni volta che nomino delle percentuali vanno intese in senso decimale: 1%=0,01).

Fin qui tutto ok (si fa per dire, sapere che la nostra banca ha solo l'1% di quanto è stato versato non è una cosa rassicurante...), se non fosse che questa quota usata per i prestiti finisce invariabilmente in un'altra banca (o anche nella stessa, perchè no), perciò una nuova frazione (1-r)*(1-r)=(1-r)² verrà prestata, finirà in un'altra banca e così via, potenzialmente all'infinito. Dunque la prima banca ha dato in prestito la quota 1-r, la seconda (1-r)², la n-esima (1-r)ⁿ, e il limite a cui tende il totale prestato è proprio una serie geometrica con x=1-r:

(1-r)+(1-r)²+... = (1-r)/r

che deriva direttamente dalla formula già vista in un commento precedente:

1+x+x²+... = 1/(1-x)

che a sua volta è il limite dalla (2) quando n tende a infinito. Quindi con la riserva frazionaria all'1% il totale prestato dal sistema bancario tende a 0,99/0,01=99 volte il totale depositato negli istituti di credito. Siccome se i soldi non sono depositati, e non sono nelle disponibilità di nessuno (nessuno diverso da un istituto di credito), tecnicamente non esistono, ne segue che questa massa di 99 volte il capitale versato è stata creata dal nulla. A riprova di ciò, il capitale in cassa nel sistema bancario è comunque sempre 1 (indipendentemente dalla riserva frazionaria in vigore), e costituisce il capitale effettivamente esistente. Attenzione, questa creazione di denaro non ha niente a che fare con il famoso Q.E. di Draghi, che è sì denaro creato dal nulla, ma da un altro nulla rispetto a quello della riserva frazionaria.

Una piccola precisazione al post precedente. Se qualcuno provasse a usare la formula (4) per confrontarla magari con un finanziamento che ha in essere, potrebbe trovare qualcosa che non torna. Non essendo entrato nei dettagli ho evitato di specificare che normalmente il tasso d'interesse e la rata non sono direttamente confrontabili, dato che il primo è generalmente annuale mentre la rata di solito è mensile. Quindi la formula (4) permette di ricavare la rata annuale di un finanziamento, se volete la rata mensile dovete dividerla per 12. In definitiva, noto l'importo da finanziare "A", il numero di anni del finanziamento "n" e il tasso d'interesse annuale "i" (è il famoso TAN), la rata mensile "R₁₂" si ricava così:

R₁₂=i*A/( 12-12*(1+i)^-n)

FranZn,
premesso che di matematica mi restano solo reminiscenze liceali, ti suggerisco un tema che seguirei o almeno proverei a seguire:
---una recensione di Les Principes du Calcul Infinitésimal di René Guénon,
electrodes.files.wordpress.com/2008/12/g...infinitc3a9simal.pdf

Grazie, comunque, della risposta, fosse pure negativa.

mil

[mlv ma10ap18 17e59]

@milvalos

Ciao, non ho capito bene se ti interessa discutere del calcolo infinitesimale in sè, o della sua interpretazione da parte di René Guénon...
...nel secondo caso dovrei prima leggermi il malloppo! Comunque ho letto la prima parte e posso già dirti che si tratta di filosofia, parlarne in termini matematici non avrebbe molto senso. Inoltre, essendo stato pubblicato nel 1946, sicuramente gli mancava tutta la parte dell'analisi non standard, che è stata sviluppata solo a partire dagli anni '60. Ebbene, non so come l'avrebbe presa Guénon, ma l'analisi non standard giustifica formalmente tutte le incongruenze che -giustamente- rileva nei concetti di Leibniz. Degli infiniti matematici ne parlavo già qui , anche in questo caso il buon René non sarebbe per nulla d'accordo.

Però permettimi brevemente che sia io a contestare un argomento di Guénon, così da chiarire cosa intendo con filosofia vs matematica (in realtà sono solo termini convenzionali, dato che tecnicamente la matematica è parte della filosofia). Nel post linkato sopra vedrai che parlo della relazione biunivoca che intercorre tra numeri naturali e numeri pari, cioè ad ogni numero naturale 0,1,2,... si può associare biunivocamente un unico numero pari. Ora per Guénon questo comporta una palese contraddizione, dato che, dice, per ogni numero pari ci sono due numeri naturali (pag.23). Beh, questo non è vero. Innanzitutto ricordo che l'associazione biunivoca fra i due insiemi è data dalla seguente funzione:

n ---> 2n

o se preferiamo, cambiando notazione: f(n)=2n.

Guénon dice che, dato che i numeri pari sono intervallati sempre da un dispari nella successione dei naturali, sono per forza la metà dei numeri naturali stessi. Se avessimo a che fare con insiemi finiti sarebbe senz'altro vero, ma sarebbe altrettanto vero che prendendo come insieme di partenza quello più piccolo, data qualsiasi funzione iniettiva tra questo e l'insieme più grande, resteranno sempre fuori metà degli elementi di quest'ultimo. Concretamente: se i due insiemi in questione sono {1,2,3} e {1,2,3,4,5,6}, ogni funzione iniettiva (cioè che ad elementi diversi del primo insieme associa elementi diversi del secondo) fra il primo e il secondo mi lascerà tre elementi del secondo senza corrispondenza nel primo. Una funzione siffatta potrebbe essere:

1 ---> 2
2 ---> 4
3 ---> 6

...che lascia 1,3,5 senza corrispondenza. In effetti possiamo prendere questa proprietà come definizione di "essere il doppio dell'altro" per insiemi finiti, e sostanzialmente è proprio quello che si fa quando si definiscono i numeri naturali in termini di logica formale. Ma quando un insieme è infinito come facciamo a dire che "è il doppio di un'altro"? L'unico modo logicamente consistente (che però Guénon non considera...) è estendere la definizione data per il caso finito agli insiemi infiniti:

L'insieme A ha il doppio degli elementi dell'insieme B se e solo se ogni funzione iniettiva tra B e A lascia senza corrispondenza un insieme di elementi C che ha tanti elementi quanti B.

Ora questa definizione è palesemente non soddisfatta quando poniamo A=numeri pari e B=numeri naturali, lo sappiamo già poichè la funzione f(n)=2n definita sopra è biunivoca (=iniettiva+suriettiva), vale a dire che anche la sua inversa f^-1(n)=n/2 è iniettiva (e pure suriettiva), ma quest'ultima è proprio una funzione iniettiva dai numeri pari ai numeri naturali. Insomma, per quanto possa sembrare strano, se vogliamo sostenere che per ogni pari esistono due numeri naturali, dobbiamo inventarci una regola ad hoc che diventerebbe paradossale se applicata ad un insieme finito, che credo sia l'ultima cosa che avrebbe desiderato René Guenon mentre scriveva il suo saggio.

Vabbè, forse non sono stato molto breve, spero che si sia capito qualcosa...comunque per quanto riguarda il calcolo infinitesimale ne parlerò volentieri, magari senza coinvolgere "l'esoterismo di René Guenon" (e i Mantra e gli Hare Hare a mille lireeee...).

PS Non so se si era capita la citazione finale:

FranZeta,
grazie della generosa risposta !, e mi chiarisco.

Matematici non ne conosco per cui, avendo apprezzato quel poco che potevo dei tuoi post, pensai bene di cogliere al volo un giudizio su un autore cui tribuisco un grande merito, sia pure limitatamente alla distinzione tra infinito ed indefinito; pure sperando che la sua posizione basilare, chiara fin dall’incipit che hai letto, se a te già ignota, destasse almeno curiosità, con ciò rendendo possibile uno scambio.

Diversamente, mi sembra che, pur considerando la matematica parte della filosofia, il tuo interesse sia propriamente matematico e ben lontano dagli esoterismi e dalle religioni in cui la filosofia tante volte sconfina.

Apprezzo tale posizione e mi limito ad osservare da una parte che, mentre la matematica è stata capace di darci un linguaggio generale che ci permette misure pratiche comuni (non sempre a proposito), la filosofia (o, meglio, le filosofie) è un insieme di sette ben poco diverse, in fondo, dalle religioni e dalle parti politiche, alle quali l’assimila anche il prestigio di personalità superiori.

E qui concludo puntando al Tema, la ricerca di un linguaggio comune a partire, ovviamente, dalla nozione più astratta.


milvalos

[mlv me11ap2018 18e44]

milvalos ha scritto: pensai bene di cogliere al volo un giudizio su un autore cui tribuisco un grande merito, sia pure limitatamente alla distinzione tra infinito ed indefinito; pure sperando che la sua posizione basilare, chiara fin dall’incipit che hai letto, se a te già ignota, destasse almeno curiosità, con ciò rendendo possibile uno scambio.

Sì, non conoscevo questa posizione sull'infinito. Non mi piace però la scelta del termine "indefinito", sicuramente in ambito matematico è infelice, dato che a un certo punto dovremmo metterci a dare la definizione di "indefinito"...
Più che altro non sono d'accordo sulle premesse, cioè quando afferma che la sua distinzione non è solo una questione linguistica. A mio avviso lo è, non avrei nessun problema a chiamare l'infinito matematico in un altro modo (Cantor stesso parlava di insiemi transfiniti, oggi si usa indifferentemente l'uno o l'altro termine), ma ciò non ne modificherebbe la sostanza. Esistono molti altri termini tecnici matematici che se interpretati semanticamente porterebbero a discussioni infinite, per esempio nell'algebra moderna si parla di anelli, corpi, campi, e addirittura ideali senza che ci siano particolari connessioni tra significato tecnico e significato metalinguistico (senza contare che molti di questi termini vengono coniati in lingue diverse, e da queste poi semplicemente tradotti letteralmente). Di contro esistono anche termini tecnici molto evocativi, per esempio quando si parla di numeri iperreali (di cui ho già parlato e parlerò ancora in relazione al calcolo infinitesimale), si definiscono monade l'insieme dei numeri infinitamente vicini a un numero dato, e galassia l'insieme dei numeri a distanza finita da questo.

In definitiva, dal mio punto di vista, la discussione sull'infinito si potrebbe risolvere in modo semplice e indolore specificando che l'Infinito, quello unico e metafisico di Guénon, lo indichiamo con la maiuscola, mentre tutti gli altri possibili infiniti, compresi quelli matematici, con la minuscola, un po' come si fa con Dio e ogni altro dio.

FranZeta, mi rispondi:

Più che altro non sono d'accordo sulle premesse, cioè quando [Guénon] afferma che la sua distinzione non è solo una questione linguistica.

Per me qui Guénon ha ragione essendosi reso conto, da matematico ma non solo, quale era, che in matematica si chiama infinito, vale a dire non-finito, quello che non-finito non è per il fatto stesso di essere riferito a qualcosa, vale a dire all’una o all’altra finitezza, nel nostro contesto i numeri.

Assodato questo possiamo anche chiamare il significante di infinito Caio e quello di non-infinito Sempronio. Per me andrebbe bene purché le inevitabili proprietà dei significanti, Caio e Sempronio, appunto, non finissero per confondere i rispettivi significati stessi, cosa molto facile tra infinito ed indefinito, termini simili e perciò distinguibili solo per lessicale convenzione.

Più avanti scrivi:

In definitiva, dal mio punto di vista, la discussione sull'infinito si potrebbe risolvere in modo semplice e indolore specificando che l'Infinito, quello unico e metafisico di Guénon, lo indichiamo con la maiuscola, mentre tutti gli altri possibili infiniti, compresi quelli matematici, con la minuscola, un po' come si fa con Dio e ogni altro dio.

Ti farò sorridere informandoti che in oltre quaranta discussioni impostate su Facebook tra il 2010 ed il 2011, e, giù di lì, in altre occasioni, pazientissimamente mi premurai di precisare che scrivevo infinito sempre e soltanto con l'iniziale minuscola a scanso di fuorvianti personalizzazioni. Mie preferenze a parte, la tua proposta è ineccepibile, salvo en passant notare che ...

... l'analogia tra i rapporti, da una parte quello tra Infinito ed infinito (nel senso di non-Infinito), dall'altra quello tra Dio e gli dei, andrebbe presa con le pinze perché gli dei non sono realtà fondamentali neanche al loro stesso vertice (Indra, Zeus, Iuppiter) o, come nel caso del dio cristiano, creatore dal nulla, sono teocratiche pastorali invenzioni della logica più elementare noncuranti.

Diversamente, il rapporto tra infinito ed indefinito (o tra Infinito ed infinito, come preferisci) consiste nel considerare l'indefinito nullo per l'infinito analogamente alla nullità dell'insieme dei numeri nello zero aritmetico.

Di conseguenza, una discussione sull'infinito potrebbe incominciare col tentare di stabilire se sia opportuno includere nel proprio pensiero il significato senza limite alcuno o pure no.

Per finire, allontanandomi con ciò dall'aspetto propriamente matematico che più ti sta a cuore, e messo da parte Guénon (i cui meriti nei miei confronti non eccedono un posto di riguardo in archivio, dal quale l'ho tirato fuori, confesso, per tentare di attaccare bottone) e l'intera sua métaphysique traditionnelle, metto in evidenza, che il significante infinito, limitato dalla sua stessa definizione come qualunque altro significante, punta, come qualunque altro significante ad esso stesso convenzionalmente equipollente, all'unico significato non concettuale, vale a dire all'assenza di limite alcuno, diversamente da tutti gli altri significanti i quali invece puntano a limiti, veri o presunti tali che si voglia.


milvalos

[mlv ve13ap18 21e39]

milvalos ha scritto: Per me qui Guénon ha ragione essendosi reso conto, da matematico ma non solo, quale era, che in matematica si chiama infinito, vale a dire non-finito, quello che non-finito non è per il fatto stesso di essere riferito a qualcosa, vale a dire all’una o all’altra finitezza, nel nostro contesto i numeri.

Mah, già qui non sono d'accordo, perchè per esempio una possibile definizione di insieme infinito è questa:

Un insieme è infinito se e solo se è possibile metterlo in relazione biunivoca con un suo sottoinsieme proprio.

Questa è una definizione matematica ben posta che non fa nessun riferimento agli insiemi numerici. Possiamo anche ignorare l'esistenza dei numeri naturali, eppure non avremmo difficoltà ad applicare la definizione, che richiede solo i concetti di insieme, sottoinsieme e relazione biunivoca. Spesso, forse un po' semplicisticamente, si definisce la matematica come la scienza che studia le relazioni astratte fra insiemi, quindi se non accettiamo gli enti necessari alla definizione qui sopra non accettiamo la matematica tout court. Poi come già detto possiamo anche usare il termine transfinito in luogo di infinito, ma non è cambiandogli nome che modifichiamo le proprietà degli insiemi che verificano la definizione data.

Ciò detto rimanderei la discussione sull'infinito-transfinito (ma indefinito non lo userò mai come termine alternativo!) a quando avrò provato ad esporre una breve introduzione al calcolo infinitesimale, così da avere a disposizione qualche esempio concreto.

FranZeta,

mi sembra di non essermi spiegato perché, per me, non è questione di terminologia né di rifiutare questo o quell'ente matematico ma di constatare che la matematica usa il termine infinito a proposito di entità qualsivoglia la cui definizione è diversa dal significato senza limite alcuno. Tale constatazione non impegna nessuno a rinunciare alla terminologia preferita mentre chiarisce il qui pro quo dal momento che il termine infinito, nell'uso ricco di molti significati, quello matematico incluso, etimologicamente riflette con precisione il significato di senza limite alcuno che in matematica (e nel senso comune) manca (per ragioni che potrebbero ben essere generalmente condivisibili). Tantomeno detta constatazione impegna ad accettare come reale, utile, o altro il significato senza limite alcuno che, a venticinque secoli di vuota distanza, voglio riaffermare.

Esemplificando, imaginiamo un Comune che, con regolare delibera, abbia cambiato il termine divieto con permesso. I malcapitati automobilisti in sosta potranno difendersi davanti al giudice di pace perché conoscono il significato di permesso diversamente dagli altri che, orbi del significato senza limite alcuno, erroneamente accetteranno come non-finitezza l'assenza di limiti eccetto almeno uno.

Infatti, a lume di naso, qualunque ente la matematica assuma, tale ente almeno un limite pur l'avrà, o mi sbaglio ?

Riporto all'attenzione la risposta :

Mah, già qui non sono d'accordo, perchè per esempio una definizione di insieme infinito è questa: [...] che non fa nessun riferimento agli insiemi numerici. Possiamo anche ignorare l'esistenza dei numeri naturali, eppure non avremmo difficoltà ad applicare la definizione, che richiede solo i concetti di insieme, sottoinsieme e relazione biunivoca. Spesso, forse un po' semplicisticamente, si definisce la matematica come la scienza che studia le relazioni astratte fra insiemi, quindi se non accettiamo gli enti necessari alla definizione qui sopra non accettiamo la matematica tout court.

milvalos

[mlv do15ap18 15e27]

milvalos ha scritto: Infatti, a lume di naso, qualunque ente la matematica assuma, tale ente almeno un limite pur l'avrà, o mi sbaglio ?

I limiti matematici sono sempre relativi a qualcos'altro, non esiste nulla che assomigli all'infinito "senza limite alcuno". Ma non è nemmeno detto che tale concetto abbia senso, sia pure a livello metafisico. Potrebbe per esempio coincidere con Dio, e non mi riferisco al dio cristiano o agli dei pagani, ma all'intelligenza da cui tutto ha origine. La quale, volendo essere onesti, potrebbe anche non esistere.

Tornando alla matematica: l'intervallo (0,1) è limitato? Certamente sì. E' insiemisticamente finito? Certamente no. Una retta geometrica è limitata? Certamente no. Insiemisticamente è più grande dell'intervallo di cui prima? Assolutamente no. In matematica il termine infinito può avere svariati significati a seconda del contesto, ma questi significati comprendono sempre un "senza limite alcuno" rispetto a qualcosa. "Senza limite alcuno" rispetto a tutto non è una definizione matematica accettabile, e secondo me anche dal punto di vista metafisico lascia parecchio a desiderare. Per dargli un senso dovresti prima definirmi cos'è "tutto", e ci sono fondati sospetti per pensare che questo tutto costituisca proprio l'infinito che vorremmo definire. Tra l'altro quando si considerano insiemi troppo "grandi" all'interno della logica formale iniziano a saltare fuori paradossi, questo porta alla distinzione fra "insieme" e "classe", il primo può essere considerato come elemento di un nuovo insieme, la seconda no.

Un esempio di classe propria è "l'insieme di tutti gli insiemi". In che rapporto si porrebbe questa classe rispetto all'Infinito (d'ora in poi coerentemente col mio pensiero inizio a scriverlo con la maiuscola)? E' più grande o più piccola? Da un lato dovrebbe essere più piccola, visto che l'Infinito è uno solo ed è l'unico ente immaginabile senza limite alcuno (sto ovviamente facendo mio il pensiero di Guénon), d'altra parte cosa mi impedisce di concepire la contrapposizione fra Infinito e Nulla? Bene, allora posso concepire un insieme che consta di due elementi: l'Infinito e l'insieme vuoto. Questo insieme appartiene alla classe di tutti gli insiemi, che quindi risulterebbe "più grande" dell'Infinito.

Da questi discorsi non se ne esce più, per questo preferisco restare nel terreno matematico. Una volta poste le definizioni non c'è più alcun dubbio sull'ente matematico considerato, questa è la prerogativa della matematica stessa. Poi uno può non accettare l'esistenza dell'infinito attuale, anche solo a livello astratto, e considerare solo l'infinito potenziale. Questa è la posizione degli antichi, ma anche di molti illustri moderni, da Cantor in poi questa visione epistemologica passa sotto il nome di intuizionismo. Va anche detto che l'intuizionismo, se perseguito fino alle estreme conseguenze, comporta la rinuncia al principio del terzo escluso, e con ciò non si perde solo la teoria degli insiemi di Cantor, ma gran parte della matematica conosciuta.

FranZeta,

col rispondermi

I limiti matematici sono sempre relativi a qualcos'altro, non esiste nulla che assomigli all'infinito "senza limite alcuno".

riconosci, com'è del tutto ovvio anche ai non matematici, che la matematica (come qualunque espressione del comune buon senso e delle sue varie estensioni) si occupa di enti ciascuno dei quali almeno un limite non può non averlo, per esempio, il limite di essere proprio quell'ente e non un altro.

Imagino, con ciò, che concordi che attribuire infinitezza ad un ente infinito solo in parte, per esempi lo spazio e il numero, non sia il massimo della terminologica accuratezza; difetto peraltro giustificabile con l'uso e questo, almeno per me, spiegabile con la vacatio infiniti inaugurata da Anassimene e terminata, per quanto credo di saperne, il secolo scorso da Guénon nel modo per me inaccettabile sul quale sorvolo.

Possiamo perciò entrare nel nocciolo del tema del senza limite alcuno del quale affermi:

Ma non è nemmeno detto che tale concetto abbia senso, sia pure a livello metafisico.

Come previsto, dissento in base allo stesso argomento di Anassimandro il quale, con parole mie, sostiene che un proposto fondamento del cambiamento è insufficiente se ha sia pure un solo limite per il fatto che quel limite, invece di permettere lo scambio tra i limiti di cui il cambiamento è costituito, con gli stessi confliggerebbe. Il pensiero di Anassimandro ci è pervenuto di seconda e di terza mano. Le reliquie, con traduzione parallela, sono accessibili a

ancientsource.daphnet.org/

più precisamente a

ancientsource.daphnet.org/agora_show_tra...cription%3Fid%3D3407

dove si legge

λέγει γοῦν διότι ἀπέραντόν ἐστιν, ἵνα μηδὲν ἐλλείπηι ἡ γένεσις ἡ ὑφισταμένη.

e, a fronte,

E dice che è illimitato perché non venga meno la generazione che ne consegue.


Traduzione per me errata nel termine generazione (γένεσις) che invece traduco con cambiamento perché qui la teologia e la biologia non c'entrano un bel nulla mentre il mio traducente è attestato dal Rocci in Platone, sia pure indirettamente, divenire, termine fuorviante perché supponentemente predica l'idea di provenienza, tutta da dimostrare. In realtà constatiamo il cambiamento e nulla altro.


INOLTRE
il senza limite alcuno, pur, ovviamente, non avendo alcun senso (senso, infatti, chiama limite) è importante non solo a quello che chiamo il grado più astratto del pensiero (GAP) ma anche a qualunque altro perché liquefa la fissazione identitaria prima animalmente / neurologicamente, poi umanamente / culturalmente inevitabile.


milvalos

[mlv lu16ap18 22e51]

Calcolo Infinitesimale (parte prima)

Ovvero Berkeley vince il primo set, Leibniz poi vince il match quando è nella tomba da due secoli

Dopo un po' di filosofia tornerei alla matematica pura, con il già promesso discorso sul calcolo infinitesimale. Siccome l'argomento sarebbe davvero vasto ho messo "parte prima" (così arriva prima, direbbe il Bergonzoni...) più che altro per dare l'impressione che tutto quello che non dico qui potrà essere affrontato più avanti, ma non è affatto detto che ci sarà una parte seconda. Dunque sistemiamoci bene sulla sedia e buttiamoci a bomba sul calcolo infinitesimale.

Iniziamo subito col dire che il calcolo infinitesimale (d'ora in poi CI) è la base di quella vasta disciplina matematica nota come Analisi, tanto che in inglese si parla di calculus tout court per riferirsi al CI. A sua volta il CI si può dividere in due discipline fondanti, il calcolo differenziale e il calcolo integrale. Due definizioni piuttosto rozze ma buone per i nostri scopi di queste discipline sono:

calcolo differenziale <----> trovare la tangente (in un punto) ad una curva

calcolo integrale <---> trovare l'area racchiusa in una curva

Entrambi trovano prodromi nella geometria antica, ma solo il calcolo integrale fu sviluppato in modo simile a quello moderno, ovviamente dai greci, in particolare Archimede fu il campione massimo della disciplina. Oltre al famoso trattato Della sfera e del cilindro, a lui si devono tutta una messe di altri risultati che coinvolgono aree e baricentri di figure curve, e fino a tempi relativamente recenti non si sapeva nemmeno bene come avesse fatto a trovare tali risultati. Poi agli inizi del '900 si scoprì un palinsesto contenente un suo trattato perduto, il Metodo, e a quel punto fu chiaro che Archimede avrebbe potuto tranquillamente scrivere un moderno testo di Analisi Matematica, almeno per quanto riguarda la parte integrale.

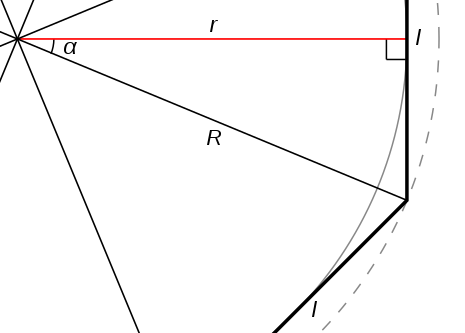
Vediamo un esempio di "integrazione" all'antica: il calcolo dell'area del cerchio. I greci, sfruttando la loro conoscenza dei poligoni regolari, notavano che indipendentemente dal numero dei lati, l'area di questi aveva sempre la stessa espressione:

A=a*P

Dove a è l' apotema e P il semiperimetro (è un facile esercizio dimostrare questa formula, guardate un po' l'immagine seguente:


tenendo conto che l'apotema è indicato con r).

Siccome più aumentiamo il numero di lati di un poligono regolare più questo si avvicina alla circonferenza circoscritta (e questa a sua volta si avvicina a quella inscritta), possiamo concludere che la formula resta valida anche per la circonferenza, che in tal modo viene vista come un poligono regolare con infiniti lati (primo infinito!). Dato che l'apotema diventa il raggio del cerchio e il semiperimetro la semicirconferenza, ecco che a*P ---> r*(π*r)=πr², e abbiamo la nota formula dell'area del cerchio. A dirla tutta i greci avrebbero lasciato indicato π come il rapporto fra circonferenza e diametro, dato che ai loro tempi il problema della "quadratura del cerchio" era ancora più che mai aperto.

Questo modo di ragionare, che viene anche detto metodo di esaustione, è sostanzialmente lo stesso che si usa nel calcolo integrale moderno, con la differenza che oggi sappiamo definire rigorosamente il concetto di passaggio al limite, cioè quel balzo che dal finito ci porta all'infinito (secondo infinito!). In realtà il concetto classico di limite non ricorre all'infinito attuale, ma solo a quello potenziale (terzo+quarto infinito!), quindi non serve riprendere da capo le discussioni fatte sopra, però come vedremo fra poco il modo di ragionare dei primordi del calcolo differenziale era ben diverso, e molto più simile a quella variante del CI che passa sotto il nome di Analisi non standard.

Ma andiamo per gradi. Come già detto il calcolo differenziale è l'altra metà del CI, il rapporto fra questo e il calcolo integrale si chiarisce solo nel 1600 quando, diversi matematici fra i quali spicca l'allievo di Galileo Evangelista Torricelli (quello del barometro), scoprono quello che oggi è noto come Teorema fondamentale del calcolo integrale, che è talmente semplice che intanto lo riporto e poi magari più tardi lo spiego:

La derivata della funzione integrale è la funzione integranda.

Al di là della terminologia, il teorema afferma semplicemente che calcolo differenziale e integrale sono uno l'inverso dell'altro, e la cosa è piuttosto sorprendente se consideriamo il significato originario delle due operazioni associate ad essi (derivazione = trovare la tangente, integrazione = trovare l'area). Con questo risultato in tasca, e con la giusta dose di genio puro e cristallino, sul finire del secolo XVII Newton e Leibniz, indipendentemente e quasi contemporaneamente, scoprono i principi del calcolo differenziale. Va anche detto che entrambi si erano basati sul metodo utilizzato da Fermat per trovare le tangenti. Insomma, qui sono coinvolti pezzi da 90 della storia della matematica.

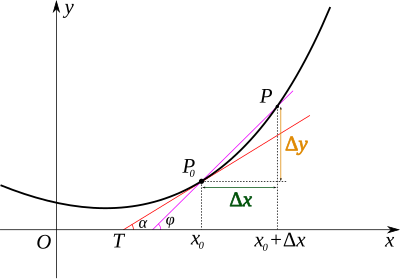
Vediamo subito come funziona questo calcolo differenziale, senza nessun preambolo, anche perchè ce ne sarebbero parecchi da fare e li trovate già tutti in un qualunque testo di Analisi 1. Mettiamo un disegnino per aiutarci:



Mi serve intanto ricordare che l'equazione di una retta passante per il punto (x₀,y₀) del piano cartesiano è la seguente:

y-y₀=m*(x-x₀)

La "m" che compare nell'equazione, detta coefficiente angolare, è il rapporto Δy/Δx delle quantità il cui significato è spiegato dalla figura. Ora ci occuperemo solo di funzioni (continue) y=f(x), il grafico della funzione è in generale una curva e il nostro intento è trovare la tangente alla curva in un suo qualsiasi punto P₀=(x₀,y₀). L'idea è che se prendiamo la retta passante per P₀ e un altro punto P sul grafico della funzione, questa si avvicinerà tanto più alla tangente quanto più P si avvicina a P₀:



Siccome P₀ sappiamo a priori che punto sia, l'unica cosa che ci serve per individuare la retta tangente è il coefficiente angolare "m", cioè il rapporto Δy/Δx quando queste quantità tendono a zero. A questo punto seguiamo Leibniz che ci dice: in luogo di Δx e Δy consideriamo le nuove quantità infinitesime (quinto infinito!) dx e dy, che hanno grossomodo lo stesso significato dei "lati della circonferenza" quando vediamo quest'ultima come un poligono regolare con infiniti lati, e facciamo il rapporto:

df(x₀)/dx= (f(x₀+dx)-f(x₀))/dx

Notiamo che se prendiamo Δx invece di dx il rapporto qui sopra è precisamente Δy/Δx. Questo rapporto, se esiste, è il coefficiente angolare della retta tangente alla funzione f punto x₀ (cioè al grafico di f nel punto P₀). Dato che x₀ è un punto generico, possiamo anche omettere l'indice e scrivere semplicemente:

(1) df(x)/dx=(f(x+dx)-f(x))/dx

che ci fornisce una nuova funzione, f'(x)=df(x)/dx, detta derivata di f, la quale punto per punto ci dà il coefficiente angolare della retta tangente ad f. NOTA LINGUISTICA: dx,dy, ecc. si leggono “de-x, de-y “, con pronuncia tedesca, mentre i rapporti dy/dx, df/dx ecc. si leggono “de-y-in-de-x, de-f-in de-x” e non “de-y-su-de-x,…” come se fosse un normale rapporto. Ciò avrà senso (se sarò bravo a spiegarmi) più avanti.

La cosa, vista così, può lasciare molto perplessi, però funziona! Facciamo un esempio pratico, prendiamo f(x)=x² e scriviamo il rapporto (1) corrispondente a questa funzione:

((x+dx)²-x²)/dx = (x²+2xdx+dx²-x²)/dx = 2x+dx

Ci ritroviamo quindi con l'espressione 2x+dx, ma siccome dx è un infinitesimo, cioè è "più piccolo di qualsiasi numero", facciamo semplicemente finta che non ci sia e otteniamo:

(x²)’=2x

L'apostrofo dopo la funzione è un'altra notazione per df/dx e si legge "f primo". Potete controllare, o fidarvi sulla parola, ma in effetti se calcolate il coefficiente angolare della retta tangente a y=x² (il cui grafico è una parabola) in un qualsiasi punto x, troverete che è proprio 2x. Proviamo con f(x)=x³:

((x+dx)³-x²)/dx =(x³+3x²dx+3xdx²+dx³-x³)/dx=3x²+3xdx+dx²

Anche qui, ignorando I termini che contengono dx e sue potenze, resta solo 3x². Abbiamo dunque:

(x³)’=3x²

Non è difficile dimostrare che in generale per i monomi vale:

(2) (xⁿ)’=nx^n-1

Così come è immediato vedere che la derivata di una somma è la somma delle derivate. La formula (2) è ben più utile di quanto possa apparire, visto che ogni funzione analitica (sono le comuni funzioni che "hanno un nome", come l'esponenziale, il logaritmo, le funzioni trigonometriche, ecc.) può essere scritta in forma di serie di potenze, a questo punto si può derivare semplicemente derivando ogni termine, e i singoli termini sono proprio monomi. Prendiamo la funzione esponenziale f(x)=e^x e calcoliamone il rapporto incrementale dato dalla (1):

(e^(x+dx)-e^x)/dx=(e^xe^dx-e^x)/dx=e^x ( (e^dx-1)/dx) =e^x

Il risultato segue dal fatto che il termine nella parentesi più grossa nella penultima uguaglianza è un limite notevole, che si dimostra essere uguale a 1. Quindi la derivazione lascia invariata la funzione esponenziale, e di conseguenza vale lo stesso anche per l'integrazione. Si tratta dell'unica funzione che gode di tale proprietà. Tempo addietro (post #10628) avevamo già incontrato l'espressione della funzione esponenziale come serie di potenze:

e^x=Σ _N xⁿ/n!=1+x+x²/2+x³/(2*3)+x⁴/(2*3*4)...

Se proviamo a derivare termine a termine questa serie, usando la formula (2) e il fatto che la derivata di una somma è la somma delle derivate, abbiamo:

d(e^x)/dx=0+1+x+x²/2+...=e^x

...cioè lo stesso risultato ricavato sopra, e ciò è cosa buona e giusta. Il primo termine del membro centrale è 0 per via del fatto che la derivata di un numero (ossia di una funzione costante) è sempre 0, come si può facilmente verificare sostituendo una costante alla f(x) della formula (1). La proprietà della funzione esponenziale di restare invariata per derivazione/integrazione è cruciale non solo nell'ambito dell'Analisi matematica, ma anche nella Fisica e nell'Ingegneria, per la ragione che vado ad esporvi. Potrebbe lasciare perplessi tutta questa voglia di scoprire la tangente ad una curva, cioè, ad un certo punto, ma chissenefrega...E invece no! Ce ne frega eccome, infatti prendiamo la traiettoria di un punto che si muove nello spazio, anzi, facciamo in un piano per semplificare un po', tanto i concetti sono gli stessi. Sia allora:

s(t)=(x(t),y(t))

la legge oraria del punto, cioè la funzione che, istante "t" per istante, ci dà le coordinate cartesiane x(t) e y(t) del punto. Fatto salvo per il nome diverso delle variabili indipendenti e dipendenti, siamo nella stessa situazione di prima, solo che adesso quella che chiamavamo "x" è diventata il tempo "t", e quella che era f sono le coordinate x e y espresse come funzioni del tempo. In definitiva possiamo ancora pensare di derivare queste funzioni, rispetto a "t" stavolta, ottenendo le due nuove funzioni:

x'(t)=dx(t)/dt
y'(t)=dy(t)/dt

Ora, dato che s(t) era la posizione istante per istante del punto in movimento, qual è il significato fisico della nuova funzione s'(t)=(x'(t),y'(t)) ottenuta per derivazione?

Siete pronti? Pronti pronti (quelli che lo sanno non suggeriscano...)?

E' la velocità istantanea!

Ecco che inizia un po' a chiarirsi l'importanza, anche pratica, della derivazione e del CI in generale.

Ma c'è dell'altro. Ripetiamo l'operazione di derivazione sulle coordinate di s'(t), che come appena visto ci dà la velocità del punto istante per istante, questa volta avremo:

x''(t)=d²x(t)/dt²
y''(t)=d²y(t)/dt²

Quella che ho appena usato è la notazione standard che indica la derivata seconda rispetto a "t", cioè la derivata della derivata. Chiediamoci allora: qual è il significato fisico di s''(t)=(x''(t),y''(t))?

Quella che abbiamo appena trovato signori è l'accelerazione istantanea.

Siccome tutta la fisica classica discende dalle tre leggi di Newton, la seconda delle quali vi ricordo è F=ma, la forza è il prodotto di massa e accelerazione, ora abbiamo gli strumenti per capire che questa equazione in realtà va considerata "ribaltata", ossia:

a=F/m ---> (3) d²s(t)/dt²=F(t)/m

Quello che sta scritto sopra è che se conosco la forza F(t) agente, istante per istante, su un punto materiale di massa m, per calcolare la traiettoria del moto del punto devo risolvere l'equazione (3), che coinvolge una doppia derivazione. Le equazioni di questo tipo sono le famose equazioni differenziali e saltano fuori praticamente dappertutto nelle applicazioni scientifico-tecniche. Ogni grandezza fisica è legata da integrazione o derivazione a qualche altra grandezza, e qui sta l'importanza della funzione esponenziale, che compare in molte soluzioni esplicite di equazioni differenziali, a motivo della sua proprietà di invarianza.

L'interpretazione fisica del CI è alla base dell'approccio di Newton al problema, tanto che in effetti quelle che noi definiamo funzioni erano per lui "flussioni", cioè delle quantità che variano nel tempo. Anche la sua notazione era diversa da quella scelta da Leibniz, mentre la seconda è stata in seguito adottata dall'Analisi e dalle applicazioni matematiche in generale, la prima è sopravvissuta come conveniente notazione per problemi di Fisica.

Veniamo ora ai problemi legati ai fondamenti del CI, così giustifico anche il sottotitolo del post. Come già segnalato di sfuggita, il procedimento legato all'equazione (1), anche se nella pratica funziona, nella teoria lascia parecchi dubbi. Qui salta fuori il vescovo George Berkeley e la sua critica al CI. Riportiamo il primo esempio di derivazione fatto sopra:

((x+dx)²-x²)/dx = (x²+2xdx+dx²-x²)/dx = 2x+dx

Il risultato, dice Berkeley, non è 2x, ma 2x+dx. Ora Leibniz ci dice di far finta che il dx non ci sia, dato che è un infinitesimo. C'è però un problemuccio: già dai tempi di Eudosso di Cnido si sa che non esiste nessun numero r tale che 0 < r < 1/n per ogni numero naturale n. Detto altrimenti, l'unico numero (non negativo) che sia minore di 1/n per ogni n è proprio -e solo- lo zero. Quindi il procedimento di derivazione consiste nel prendere una quantità dx, considerarla prima diversa da zero (le prime due uguaglianze), e poi porla uguale a zero (il dx che scompare dal risultato). Insomma, dx=0 sì o no? In entrambi i casi il risultato "2x" della derivazione è logicamente inconsistente.

Leibniz sapeva bene che tecnicamente Berkeley aveva ragione, ma il suo intuito gli suggeriva che il metodo era corretto, era se mai la nostra concezione dei numeri ad essere incerta. In effetti non aveva tutti i torti, dato che la teoria dei numeri reali arriverà solo un paio di secoli dopo, però per l'appunto c'era già la teoria dei rapporti di Eudosso, insomma, non è che nel primo '700 il concetto di numero fosse sconosciuto. Comunque in definitiva Leibniz suggeriva che questi infinitesimi -dx,dy eccetera- fossero delle entità a metà fra numero e non-numero, nel senso che non aveva idea di come si potesse definirle in un modo logicamente consistente, e però credeva nella loro esistenza come enti matematici. Nel frattempo Berkeley lo spernacchiava, con la logica (momentaneamente) dalla sua parte.

Nonostante l’inconsistenza logica, il CI si dimostrò da subito così straordinariamente potente da lasciarsi subito alle spalle ogni obiezione formale à la Berkeley, tanto che nell’arco di un secolo si era così sviluppato da raggiungere ogni campo delle scienze esatte. Solo nel corso dell’800 iniziò a sentirsi sempre più pressante un bisogno di sistemazione dei fondamenti, per la verità non solo del CI ma piuttosto dell’intera matematica, per quanto riguarda però il nostro ambito si trovò una soluzione grazie alla formalizzazione del concetto di limite. Sorvolerei sull’argomento, dato che pure questo fa parte del bagaglio comune ad ogni testo di Analisi, dirò solo che questa sistemazione tradisce lo spirito dello sviluppo impetuoso dell’Analisi, che è poi quello delle origini di Leibniz.

In particolare il rapporto dy/dx espresso dalla (1), in questo approccio, non è da considerarsi come un rapporto, ma una comoda scrittura che va presa come un tutt’uno, cioè un “d/dx” da applicare a una funzione “y”. Questo è un punto su cui si usa insistere molto, e chi ha studiato analisi dovrebbe averne parecchi ricordi, perché il fatto è che quasi sempre questo caveat sembra senza altro scopo che confondere le idee allo studente, dato che le cose funzionano benissimo considerando dy/dx come un vero e proprio rapporto. E’ anche opinione comune di molti storici della matematica che se questa sistemazione logica del CI fosse stata raggiunta prima, probabilmente lo sviluppo del calcolo stesso ne sarebbe stato fortemente influenzato in negativo.

Ecco però che verso la fine della nostra storia avviene un colpo di scena. Tutto nasce da arcani risultati della logica formale degli anni ’30, quando l’Analisi matematica aveva già definitivamente l’impostazione che si studia anche oggi nei corsi universitari. Ci si accorse infatti che, a partire dagli assiomi che definivano i numeri reali, era possibile costruire un altro insieme numerico ben più vasto ed enigmatico. Questo insieme, che oggi chiamiamo insieme dei numeri iperreali (indicato con *R), oltre ad avere le stesse proprietà dei numeri reali, e a contenere tutti i numeri reali, conteneva anche altri numeri che si comportavano in modo piuttosto strano. Alcuni di questi nuovi numeri risultavano essere maggiori di ogni numero reale, cioè erano da considerarsi numeri infiniti (sesto infinito!), ma dato che per ogni numero reale r esiste un inverso 1/r, e dato che i numeri iperreali hanno le stesse proprietà dei reali, per ogni numero iperreale infinito ω dovrà esistere un inverso 1/ω.

In realtà ci volle ancora qualche decennio, e almeno un altro matematico di genio, Abraham Robinson, ma alla fine diventò chiaro che questi numeri del tipo 1/ω erano proprio gli infinitesimi che aveva cercato invano di definire Leibniz. Hanno infatti la proprietà cruciale 0 < 1/ω < 1/n per ogni numero naturale n, oltre a ciò vale anche un’altra bellissima proprietà, cioè che ogni numero iperreale finito si può scomporre in modo univoco come somma di un numero reale r e di un infinitesimo 1/ω. Detto altrimenti ogni numero iperreale finito è infinitamente vicino (settimo infinito!) ad un solo numero reale.

Queste due proprietà danno immediatamente un fondamento logico inattaccabile al procedimento di Leibniz, basta usare un semplice accorgimento, ovverosia modificare la (1) come segue:

(*1) df(x)/dx=std( (f(x+dx)-f(x))/dx)

dove std(…) sta a indicare la funzione parte standard, cioè quella funzione che ad ogni numero iperreale finito associa la sua parte reale. Questa funzione è del tutto analoga alla funzione parte intera di un numero reale x (si indica [x]), che è quella funzione che per esempio a π associa il numero intero 3. Tornando al nostro famoso esempio le cose adesso vanno così:

d(x²)/dx=std(2x+dx)=2x

e non c’è più critica di Berkeley che tenga, poiché ora dx è un infinitesimo definito rigorosamente in termini di assiomi della logica formale, e anche la sua “scomparsa” dal risultato finale è perfettamente giustificata dall’utilizzo della funzione “parte standard”. Questo approccio al CI prende il nome di Analisi non Standard e a differenza dell'approccio classico, non lo troverete in nessun testo di Analisi matematica, nè in nessun corso universitario. Gli analisti (matematici s'intende) nutrono infatti un'ostinata avversione per questo modo di fondare la loro materia, quindi sebbene siano passati una cinquantina d'anni dalla sua prima formulazione l'Analisi non standard continua ad essere relegata a curiosità matematica, quando a mio avviso è di gran lunga superiore alla formalizzazione standard dell'Analisi.

A volte il parossismo nei confronti dell'Analisi non standard raggiunge vette notevoli, date un'occhiata a questo pdf , l'esempio in fondo a pag.14 mostra la risoluzione di un'equazione differenziale col metodo ribattezzato dall'autore urang-utang (si tratta in realtà del metodo non-standard dove viene omesso il passaggio finale alla funzione parte standard), poi confrontato con la soluzione ottenuta con il metodo standard, quello rrrigoroso...Se guardate bene, più avanti, in una noticina a pag.20, l'autore pare degnarsi di constatare che esiste un approoccio che dà senso a tutto ciò che ha deriso fino a quel punto, salvo poi metterlo subito da parte, visto che:

...sono convinto che la quasi totalità di chi pensa alla derivata
come rapporto tra infinitesimi non è in grado di utilizzare l’analisi non standard! Ammesso
che sappia che esista.

Cazzo, magari se iniziate a insegnarla nelle scuole, la gente saprà che esiste e potrà apprezzare il metodo nella sua semplicità antica, con l'aggiunta del rigore moderno. Ma finchè i soloni della materia continueranno a considerare l'Analisi non standard come una sofisticata giustificazione del perchè i metodi che ci dicono essere sbagliati funzionano, i poveri studenti dovranno continuare a mandare giù tonnellate di definizioni epsilon-delta e robe simili.

Per concludere, chi volesse approfondire può consultare un qualunque testo di Analisi matematica, seguono tutti lo stesso percorso di introduzione al CI. Oppure, se non dovete sostenere un esame universitario ma solo la vostra curiosità, potreste pensare di consultare questo splendido testo che è per giunta disponibile aggratis, anche se non esiste traduzione italiana, per quanto ne sappia. Direi che come prima (e forse unica) parte può bastare così.

FranZeta,

grazie dello spazio concesso
e buon proseguimento !

milvalos

[mlv lu30ap18 00e29]

Tre teoremi che più generali non si può

'e='e◦e'=e' !!!

Quello qui sopra non è un emoticon surrealista, bensì un teorema dell'algebra astratta, probabilmente fra i più generali che si possano enunciare. Volendo essere precisi sarebbe proprio la dimostrazione del teorema, ma una volta chiarito il significato dei simboli l'enunciato vi è contenuto. Purtroppo per chi legge questi chiarimenti non potranno essere concisi quanto la scrittura qui sopra, quindi chi vuole seguire il ragionamento deve avere un pochino di pazienza, ma farò del mio meglio per andare al sodo in fretta.

Come ogni edificio necessita un terreno preesistente su cui poggiare le proprie fondamenta, l'edificio matematico non fa eccezione. Già Euclide nei suoi Elementi segue questa strada, premettendo all'inizio dell'opera una lista di nozioni comuni e postulati, che sono un po' terreno e un po' fondamenta del suo edificio. Oggi le cose sono più complicate, ma schematizzando possiamo dire che le fondamenta della matematica moderna sono costituite dalla logica matematica, mentre le fondamenta di quest'ultima sono l'equivalente del terreno preesistente alla costruzione. Cosa sono dunque queste fondamenta ultime? Innanzitutto il linguaggio naturale, cioè l'italiano corrente nel nostro caso, o qualunque altra lingua che ci permetta di descrivere dall'esterno (dell'edificio) ciò che stiamo facendo, e che ci consenta di definire le nostre nozioni comuni, che non sono quelle di Euclide, ma sono ad esempio il concetto di insieme, di elemento, e la relazione di appartenenza.

L'algebra moderna, che nell'edificio matematico è solo un gradino sopra la logica nella scala della priorità epistemologica, si accontenta di partire da oggetti così generali e non definibili formalmente (in quanto enti primitivi) quali gli insiemi. Si parla di struttura algebrica quando abbiamo un insieme dotato di una legge di composizione interna, vale a dire un'operazione che presi due qualsiasi elementi dell'insieme ne associa loro un terzo. Le classiche operazioni di addizione e moltiplicazione su un insieme numerico sono l'archetipo di legge di composizione interna, ma le strutture algebriche possono essere di tipo infinitamente vario. Un esempio più esotico è dato dall'insieme delle stringhe di testo che si ottengono con i caratteri dell'alfabeto latino (chiamate "parole" anche in ambito matematico, con la differenza che qui anche "XHBUJHGD" va considerata una legittima parola), dove l'operazione consiste nella semplice giustapposizione, così che CASA+CHIESA=CASACHIESA.

Siccome a questo livello di generalità si preferisce non usare simboli che abbiano uno specifico significato, ecco che adotteremo un simbolo neutro per indicare l'operazione di una struttura algebrica, per esempio "◦" (e con ciò un primo simbolo nel teorema d'apertura assume significato...). Può accadere che una struttura algebrica possieda elementi con la particolare proprietà di non incidere sull'operazione, cioè elementi "e" tali che:

e◦a=a

per ogni altro elemento "a" della struttura. Questi elementi sono detti elementi neutri per ovvie ragioni. Nel caso delle operazioni + e x dell'aritmetica gli elementi neutri sono rispettivamente 0 e 1, mentre nella struttura data dalle stringhe di caratteri alfabetici l'elemento neutro è rappresentato dalla stringa vuota. Attenzione: non è la barra spaziatrice, la stringa vuota è proprio un carattere nullo, sarebbe un tasto che non ha effetto sullo schermo, o se preferiamo il cursore che lampeggia in attesa di un nuovo carattere.

Adesso serve una precisazione. La proprietà commutativa, ossia quella che ci garantisce che a◦b=b◦a per ogni coppia di elementi (a,b), è una proprietà molto specifica che al nostro livello di generalità non possiamo assumere, quindi occorrerà fare distinzione fra elementi neutri a sinistra ('e) ed elementi neutri a destra (e'), definiti dalle seguenti identità:

'e◦a=a
a◦e'=a

Questa distinzione è doverosa dato che, non valendo la proprietà commutativa, in generale 'e◦a non sarà uguale ad a◦'e, e lo stesso dicasi per e'. Un elemento che sia neutro sia a destra che a sinistra viene detto elemento neutro tout court. Ora abbiamo gli strumenti per enunciare il nostro teorema iniziale:

TEOREMA 1. Se in una struttura algebrica (A,◦) esiste sia un elemento neutro a sinistra 'e che un elemento neutro a destra e', allora questi coincidono.

La coppia (A,◦) identifica la struttura algebrica: A è l'insieme su cui è definita e ◦ l'operazione della struttura. La dimostrazione del teorema è quella data nell'incipit del post: consideriamo infatti la composizione dei due elementi neutri 'e◦e', questa è evidentemente uguale a 'e perchè e' è neutro a destra, ma anche ad e' dato che 'e è neutro a sinistra. Sembra una banalità, ma vi invito a riflettere sull'estrema generalità delle ipotesi e sull'affermazione molto circostanziata del teorema: è quasi un miracolo che in tale situazione si possa già dimostrare qualcosa! Dal Teorema 1 discende immediatamente un corollario, anch'esso piuttosto profondo:

COROLLARIO (TEOREMA 1). Una struttura algebrica ammette al più un elemento neutro.

La dimostrazione del corollario è immediata dato che un elemento neutro "e" è per definizione neutro sia a sinistra che a destra, quindi due elementi neutri e₁, e₂ devono per forza coincidere (basta anche qui considerarne la composizione e₁◦e₂). Bene, teorema e corollario appena dimostrati sono fra i più generali dell'algebra e dell'intera matematica. Ce ne sono altri simili, che richiedono solo qualche semplice ipotesi aggiuntiva. Consideriamo ad esempio la proprietà associativa, che finora non abbiamo incluso nelle ipotesi. Un'operazione si dice associativa se vale:

a◦(b◦c)=(a◦b)◦c

cioè se vale la semplificazione della parentesi, in tal caso è lecita la scrittura a◦b◦c in luogo delle due qui sopra con le parentesi. Può ora accadere che in una struttura algebrica associativa (esisterebbe tutta una terminologia tecnica per distinguere le strutture algebriche sulla base delle proprietà verificate, non mi sembra il caso di parlarne qui), dotata di elemento neutro "e", presi due elementi a,b risulti a◦b=e. In tal caso si dice che "a" è l'inverso sinistro di "b", e simmetricamente "b" l'inverso destro di "a". Preso un qualsiasi elemento "a" della struttura, usiamo le notazioni *a e a* per indicarne rispettivamente l'inverso sinistro e destro. Ecco allora il nostro secondo teorema-che-più-generale-non-si-può:

TEOREMA 2. Sia (A,◦) una struttura algebrica associativa dotata di elemento neutro e, se l'elemento a ammette sia un inverso sinistro *a che un inverso destro a*, allora questi coincidono.

dimostrazione:

Come noterete in questo caso la dimostrazione è un po' meno immediata, così ho numerato le righe per spiegare i passaggi. Innanzitutto abbiamo una catena di uguaglianze che ci porta dall'inverso sinistro *a a quello destro a*, stabilendone così l'identità, vediamo ora come. La riga 1 è semplicemente un'applicazione della definizione di elemento neutro, la riga 2 un'analoga applicazione della definizione di inverso destro, il passaggio 2--->3 è invece cruciale, ed è qui che abbiamo bisogno dell'ipotesi della proprietà associativa, senza quella non c'è la riga 3 e nemmeno il teorema. La riga 4 infine è perfettamente simmetrica alla 1, una banale applicazione di definizioni.

Consideriamo ora una struttura ancora un po' più complessa, o meglio uniamo due strutture algebriche costruite sullo stesso insieme A: abbiamo allora una cosa del tipo (A,♂,♀), dove ♂ e ♀ sono due distinte operazioni sullo stesso insieme. Strutture di questo tipo possono godere della fondamentale proprietà distributiva che lega le due leggi di composizione:

a ♀ (b ♂ c)=(a ♀ b) ♂ (a ♀ c)

Scritta così sembra incomprensibile, ma se usiamo le solite operazioni aritmetiche + e x è semplicemente:

a x (b+c)=(a x b)+(a x c)

Possiamo allora enunciare un ulteriore teorema generalissimo:

TEOREMA 3. Sia (A,♂,♀) una struttura algebrica con due operazioni associative legate dalla proprietà distributiva. Supponiamo che l'operazione ♂ sia dotata di elemento neutro e_♂, e supponiamo inoltre che ogni elemento a dell'insieme A abbia un inverso rispetto all'operazione ♂. Allora per ogni a in A si ha:

a ♀ e_♂ = e_♂.

Anche qui, se al posto di ♂ e ♀ dicessimo + e x, il Teorema 3 afferma che a x 0 = 0 per ogni a. Cioè un numero moltiplicato per zero fa sempre zero. Beh, come vedete, e come dimostreremo subito, la cosa è assai più generale dell'ambito aritmetico.

dimostrazione:

(Siccome in fondo non vi voglio proprio male, uso i simboli + e x che tanto ci sono cari, a questo punto credo sia ormai chiaro che usando ♂ e ♀ funzionerebbe allo stesso modo, salvo il fatto che non si capirebbe un accidenti. Attenzione: l'inverso di "a" rispetto a "+" in quanto segue diventerà "-a", cioè quello che è comunemente l'inverso di "a" rispetto all'addizione. Analogamente userò "0" in luogo di e_♂ per indicare l'elemento neutro della prima operazione.)

a x 0 = a x (a - a) = a x a - a x a = b - b = 0

Breve spiegazione. Anche in questo caso c'è una catena di uguaglianze che stabilisce l'identità del primo e dell'ultimo membro, che è l'enunciato del teorema. Il secondo e il terzo membro sono uguali per via della proprietà distributiva, mentre l'ultima uguaglianza b - b = 0 (che in realtà è a scopo chiarificatore, ma sarebbe facoltativa) si giustifica come segue. Non sappiamo quanto faccia a x a, dato che non abbiamo fatto nessuna ipotesi su cosa possa essere l'elemento "a" nè l'operazione "x" (che poi sarebbe ♀ se avessi voluto infierire), però sappiamo per ipotesi che deve per forza essere un elemento dell'insieme A, e noi allora lo chiamiamo "b". Quindi a x a - a x a = b - b. Ma b - b è la composizione di un elemento e del suo inverso (rispetto all'operazione +), quindi, sebbene non abbiamo idea di quale elemento sia e nemmeno di quale operazione stiamo facendo, sappiamo comunque che deve fare 0, per definizione di elemento inverso.

Relativamente alla relatività galileiana

(Qualche precisazione al topic "Terra Piatta: dibattito")

Dato che il thread Terra Piatta: dibattito è stato impostato come discussione a due, uso questo spazio per ripristinare un certo grado di verità fisica in alcune affermazioni del suddetto forum. Mi pare anche il caso di premettere che, così come in quella sede il dibattito è impostato in modo da escludere tutti gli altri utenti, in questa sede prego di non intervenire se non per chiarimenti o perchè si è veramente informati sul tema. Senza nessun intento polemico, gradirei solo che non ci fossero interventi ad mentula canis.

Veniamo ora al problema. La situazione è quella di un aereo che vola a una certa quota, in modo che la portanza generata dalle ali sia esattamente uguale e opposta alla forza di gravità, cito da un commento:

1- Una volta che l'aereo è in volo ovvero ha sviluppato abbastanza portanza da annullare la forza di gravità, quest'ultima non ha possibilità di interferire in nessun altra maniera con il “sistema aereo” perciò l'aereo sarà in grado di viaggiare perfettamente in linea retta.

Concentriamoci sulla figurina centrale, quella relativa alla posizione iniziale, poichè le altre due sono inferenze scorrette. In quest'altro commento si legge poi la seguente precisazione:

La forza risultante mentre un aereo vola è esclusivamente quella motrice che spinge l'aereo in avanti. La FdG è completamente azzerata/bilanciata dalla portanza, quindi secondo la relatività galileiana non è possibile avere una variazione della traiettoria.
Secondo Galileo, infatti, l'aereo semplicemente deve procedere in linea retta. Seguire la circonferenza della terra significherebbe seguire una linea curva.

Se vuoi che la gravità generi una accelerazione verso il basso, allora la portanza creata dall'aereo deve essere inferiore di quel tanto che basta, ovvero dovrebbe essere una scelta volontaria del pilota o del sistema di navigazione. Non mi risulta che si voli in questo modo anche perché la variazione di altitudine dovuta alla caduta dell'aereo, non incide sul beccheggio.

La seconda parte della citazione potrebbe generare confusione, perchè quello che conta nel discorso non è che a bilanciare la gravità sia la portanza, ma che ci sia una forza che istante per istante è uguale e contraria, qualunque sia la sua natura. Il discorso che andiamo a fare in effetti vale anche per i satelliti, che come è noto non stanno in quota grazie alla portanza. Allora, partiamo da Galileo e dal suo principio di inerzia: un corpo non soggetto a forze si muove di moto rettilineo uniforme. Bene, dato che nel post Calcolo Infinitesimale qui sopra ho introdotto il rapporto esistente fra Analisi e Fisica, possiamo usare i concetti già esposti e quindi partiamo dal fatto che l'accelerazione è la derivata seconda dello spazio rispetto al tempo.

In assenza di forze siamo nella situazione F=ma=0, quindi l'accelerazione a è zero (altrimenti dovrebbe essere zero la massa m, cioè non ci sarebbe alcun corpo di cui discutere). Ricordo che la posizione di un corpo istante per istante è data dalla sua legge oraria , se per semplicità ipotizziamo che il moto si svolga in un piano questa avrà la forma:

s(t)=( x(t),y(t))

dove la variabile t indica il tempo e x(t), y(t) sono due funzioni che forniscono le due coordinate cartesiane che il corpo occupa all'istante t. Con ciò ovviamente il corpo si suppone puntiforme, altra semplificazione molto vantaggiosa nel nostro caso. Dunque dicevamo che l'accelerazione è nulla, questo si traduce nelle due equazioni (differenziali, ma non spaventatevi...):

d²x/dt²=0
d²y/dt²=0

...cioè le derivate seconde rispetto al tempo sono identicamente nulle. La soluzione generale del sistema di equazioni è:

x(t)=v_0xt+s_0x
y(t)=v_0yt+s_0y

dove v_0x, v_0y sono due costanti che hanno il significato fisico di velocità iniziale lungo l'asse x e y rispettivamente, mentre s_0x e s_0y rappresentano la posizione iniziale del punto, in coordinate cartesiane ovviamente. Quella descritta dalle equazioni qui sopra è una retta che il punto percorre con velocità costante v=sqrt(v_0x²+v_0y²) al variare del tempo t, e nell'istante iniziale t=0 il punto si trova in (s_0x,s_0y). Ecco allora che abbiamo dedotto il principio d'inerzia, già enunciato sopra, via passaggi puramente matematici direttamente dall'ipotesi che non ci siano forze agenti sul corpo .

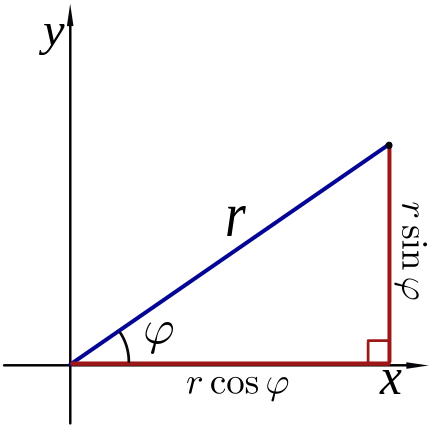
Questa però non è la situazione dell'aereo descritta all'inizio. Per rendersene conto è conveniente passare alle coordinate polari r(t),φ(t) legate alle x(t),y(t) dalle relazioni riportate in figura:


A questo punto il fatto che la forza di gravità sia esattamente compensata dalla portanza si traduce nella seguente equazione differenziale:

d²r/dt²=0

che ci dice che l'accelerazione lungo la componente radiale r(t) è sempre nulla. La soluzione generale in questo caso è:

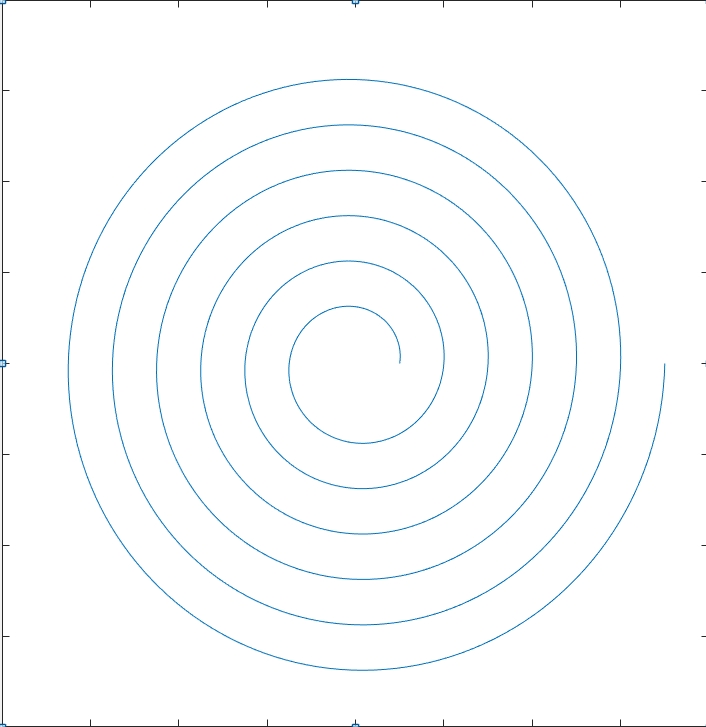
r(t)=v_0rt+r₀

con v_0r e r₀ rispettivamente velocità e posizione radiale iniziale, soluzione che non corrisponde a una linea retta, bensì a una spirale:



Per tracciare il grafico sopra ho posto v_0r e r₀ uguali a 1. Questa come dicevo è la soluzione generale, ma nel nostro caso sappiamo che v_0r=0, perchè all'istante iniziale l'aereo vola perfettamente livellato, ecco allora che la nostra spirale diventa una circonferenza di raggio r₀, che sarebbe poi la somma della quota dell'aereo e del raggio terrestre. Non solo: il fatto che la forza di gravità sia costante in modulo (a una data quota di altezza) ci porta a concludere che anche il moto angolare deve essere costante:

φ(t)=ω₀t+φ₀

dove ω₀ è la velocità angolare e φ₀ la posizione (angolare), entrambe all'istante iniziale t=0. Il nostro aereo si muove dunque di moto circolare uniforme, in accordo con la relatività galileiana. Va precisato che in effetti se l'accelerazione radiale è uguale a zero significa che la forza di gravità è uguagliata dalla somma della portanza e della forza centrifuga dovuta al moto circolare. In quanto precede ho tralasciato quest'ultima forza poichè:
- nel caso dell'aereo è del tutto trascurabile;
- avrei rovinato la "sorpresona" finale nello scoprire un moto circolare;
- sarebbe stata una complicazione inessenziale.
Tuttavia nel caso del moto di un satellite, essendo pari a zero la portanza, sarebbe solo la forza centrifuga a intervenire per controbilanciare la gravità.

***********************

Chiarito come si imposta il problema fisico dell'aereo, mi sembra il caso di fare una precisazione anche sul discorso del pendolo di Foucault, che è stato liquidato in modo sbrigativo. Il pendolo di Foucault infatti non si limita a ruotare, ma ruota con una velocità angolare proporzionale alla latitudine. Per la precisione la rotazione oraria del pendolo è data da:

α=360°/24*sin(λ)

dove λ è la latitudine alla quale il pendolo è posizionato. Alle nostre latitudini (45°) la rotazione α è di 10.6° ogni ora. Si noti che nell'emisfero australe la formula comporta una rotazione invertita, cosa che si verifica sperimentalmente. Quindi la sfericità della terra è una conseguenza indiretta dell'esperimento di Foucault: deriva dal fatto che sperimentalmente si ottengono velocità di rotazione proporzionali a sin(λ), se gli esperimenti avessero evidenziato che la rotazione è indipendente dalla latitudine, beh, quella sarebbe stata una prova che la terra gira, ma è piatta.

Michele Pirola ha scritto:

Cos'è il Genio?
È fantasia, intuizione, colpo d'occhio e velocità d'esecuzione.

FranZeta ha scritto:

Michele Pirola ha scritto:

Cos'è il Genio?
È fantasia, intuizione, colpo d'occhio e velocità d'esecuzione.

:laugh: . Ce ne ho un'altra di vignetta che però è in inglese. Penso si capisca (se qualcuno non la capisse poi gliela traduco):