Le caratteristiche di luminosità della superficie lunare

Facciamo un passo alla volta:

con th_i=0:

La prima parte della formula di Hapke (53): diventa cosi`:
Che ha il minimo (.5) con th_r=0 , e 1 con th_r=+/- 90.

e` corretto? questa parte a che cosa corrisponde, fisicamente?

Il primo termine dell'equazione di Hakpe è la legge di Lommel-Seeliger . Nel caso da te esposto, che è corretto, la sorgente illumina la superficie perpendicolarmente (th_i = 0), e quando l'osservatore è in linea con la sorgente (th_r=th_i, g=0) esso osserva/misura una quantità di luce che è la metà della luce incidente. La quantità di luce osservata/misurata aumenta con l'aumentare dell'angolo di osservazione, e quindi dell'angolo di fase, fino ad arrivare al massimo quando l'asse di osservazione è perpendicolare alla normale della superficie, e l'osservatore osserva/misura la stessa quantità di luce che incide sulla superficie.

Ho scritto un programmino (numpy) per testare le formule su di una superficie sferica:

spiego come ho calcolato gli angoli che ci interessano:

con:

il risultato e` questo:



Se ho capito bene, con th_r si tiene conto di una variazione di luminosita` dovuta alla prospettiva? l`effetto aumenta all`aumentare dell`angolo di campo e della distanza dal centro immagine?

theta_r tiene conto della posizione dell'osservatore rispetto alla superficie quindi in un certo senso alla prospettiva. Poniamo per una superficie le seguenti definizioni



N = normale locale della superficie
V = versore di osservazione
L = versore di illuminazione

theta_r = acos( dot(N,V) )
theta_i = acos( dot(N,L) )

Da quel che mi è parso di capire, tu fai correttamente variare la normale locale da punto a punto sulla superficie della sfera, quindi gli angoli theta_i e theta_r cambiano da punto a punto. Ora usando le GLSL e implementando la BRDF di Lommel-Seeliger ottengo, nel caso di una sfera, che la reflactance R è



dove in caso di luna piena la luminosità appare costante su tutto il disco, mentre la BRDF (R/theta_i) è



dove la luminosità cresce verso il contorno; cosa che a prima vista mi pare più simile a quello che hai ottenuto tu nella tua immagine della luna piena, quindi c'è qualcosa che non mi torna, a meno che non sia solo un effetto dovuto al maggior contrasto dello sfondo nero. In aggiunta mostro un confronto con la funzione di Lambert



La cui BRDF è una costante, ma la R sulla sfera mostra una riduzione di brightness verso il contorno.

Nell`immagine che ho allegato non ho applicato la legge di Lambert del coseno; moltiplicando R per m0 ottengo (in scala di grigi e in falsi colori):



Per la prospettiva intendo questo: prendiamo ad esempio tre casi (trascurando eventuali fenomeni di diffrazione):

1) fotografia diretta e centrata del Sole in un ambiente senza atmosfera
2) foto di una superficie lambertiana
3) ripresa di un altro tipo di superficie

nel caso:

1) entrano in camera solo i pochi raggi perpendicolari al piano del sensore (punti centrali=1, altri=0)
2) entrano in camera raggi da tutte le direzioni (punti illuminati=cos(th_i))
3) eventuale variazione di illuminazione dovuta a th_r_uv, intendendo con uv la posizione di ogni elemento del sensore (punti illuminati=f(th_r_uv)*cos(th_i))

voglio dire: non conta solo l`angolo di ripresa (puntamento propriamente detto), ma anche quello di ogni singolo raggio entrante nella camera.

Ho capito cosa intendi. La funzione R serve solo ha calcolare lo scattering della superficie illuminata dal Sole. L'equazione completa (light transport) per un generico punto p è questa



Dove f è la BRDF (R/cos(theta_i)), Li è la radianza incidente sulla superficie, Le è la radianza emessa dalla superficie e Lo è la radianza osservata. Le radianze sono definite in funzione degli angoli sferici di incidenza omega_i e di osservazione omega_o, entrambi sono esprimibili come una funzione di theta e phi. L'integrale è calcolato sulla superficie sferica centrata in p rispetto all'angolo sferico omega_i. Penso sia l'unico modo per ottenere il risultato corretto, che in false color è questo:



Ovvero una distribuzione uniforme di luminosità. Qui però ci stiamo spingendo verso il ray-tracing + radiosity di cui io conosco solo a grandi linee i processi e gli algoritmi. Se sei interessato ho un libro molto corposo sull'argomento che spiega teoria, algoritmi e tecniche, basta che mi mandi un mp e te lo passo.

La mia immagine dovrebbe essere sbagliata anche perche` e` una ripresa relativamente vicina: in questo modo non si fotografa una semisfera completa, ma solo una calotta.



In piu`, negli angoli dell`immagine i raggi sono fortemente angolati (oltre 20 gradi).

Allungando la focale, l`illuminazione della superficie si uniforma senza dover moltiplicare per m0:



Ci devo meditare sopra: bisogna moltiplicare o no per m0?

p.s. il programma mi ha cambiato la corrispondenza colori/valore: nell`immagine del messaggio precedente (R*m0) il centro vale .5 e la periferia .3 circa; in questa (R) i valori sono rispettivamente .5 (centro) e .6 circa (esterno).

Sono passati tre anni credo dal mio ultimo post.
Colgo l'occasione per salutare l'utenza di LC,specialmente utenze da molto svanite.
Detto questo,LC è forse l'unico posto su internet, che mi faccia rendere conto di quanto si possa essere ignoranti su molte tematiche.
Grazie a doktorenko e kamiokade per divulgare e condividere il loro sapere.
Merce rara

La luminosità del disco quando g = 0 deve essere uniforme per qualunque lunghezza focale. In ogni caso la formula corretta è quella che ho postato in precedenza, dove Le è zero perché la sfera non emette luce propria ma diffonde la luce proveniente dalla sorgente, ovvero rimane solo l'integrale. Nel caso in questione abbiamo che la funzione di Lommel-Seeliger è µ0/(µ0 + µ), quindi la BRDF associata che va nella formula è 1/(µ0 + µ), ma che nell'integrale si rimoltiplica per µ0 ritornando la funzione di partenza. Quindi la R non va moltiplicata per µ0, ma rimane così com'è fin tanto che µ0 > 0, se µ0 < 0 la funzione va cambiata di segno. È possibile che nel caso della sfera si ottenga comunque un risultato corretto anche senza integrare l'irradianza ( Li*abs(µ0) ) per la BRDF ( 1/(µ0 + µ) ), ma penso che sia solo un caso.

Nichiren ha scritto: Sono passati tre anni credo dal mio ultimo post.
Colgo l'occasione per salutare l'utenza di LC,specialmente utenze da molto svanite.
Detto questo,LC è forse l'unico posto su internet, che mi faccia rendere conto di quanto si possa essere ignoranti su molte tematiche.
Grazie a doktorenko e kamiokade per divulgare e condividere il loro sapere.
Merce rara

Ti ringrazio, e parlando per me stesso, si fa quel che si può. Rispetto a questi temi io sono un autodidatta, perciò la mia competenza è molto limitata, comunque in generale l'ignoranza è una malattia che si può combattere, anche se non la si sconfigge mai del tutto.

Nel caso di una sfera perfettamente liscia, ogni punto non è illuminato solo direttamente? non vedo come possa essere colpito da raggi di luce rimbalzanti da altri punti della stessa superficie.

Per prospettiva intendo, più che la lunghezza focale, il diametro angolare dell'oggetto ripreso: nel caso della Luna è molto piccolo (mezzo grado) quindi non dovrebbe avere molto effetto sull'illuminazione, ma nell'immagine #15462 la sfera è vicina e occupa quasi tutto il campo (45 gradi).

Perdonami doktorenko penso di essermi espresso male. L'equazione che ho riportato è del tutto generica, Le è la luce emessa dalla superficie se fosse anche una sorgente di luce, mentre Li è la luce incidente sulla superficie, che proviene da qualunque fonte diretta o indiretta, che viene diffusa (verso l'osservatore e le altre superfici circostanti) in accordo alla BRDF propria della superficie. Per la sfera, che è convessa, illuminata da una sola sorgente di luce, il termine Li si riferisce solo alla sorgente di luce poiché, come ha detto giustamente tu, la superficie della sfera non partecipa all'illuminazione ma diffonde la luce verso l'osservatore. Per una semisfera illuminata all'interno, Li sarebbe composto sia dalla luce diretta della sorgente che la luce indiretta della superficie stessa.

Ti consiglio di leggere questo documento Geometrical Considerations and Nomenclature for Reflectance , che spiega nel dettaglio il caso di una superficie generica illuminata da una sorgente generica di luce e con radianza Li, mi ha aiutato parecchio nella comprensione delle BRDF e della terminologia associata.

Riguardo alla sfera da te disegnata sono abbastanza sicuro che debba essere uniforme indipendentemente dalla posizione dell'osservatore purché g sia 0, controllo e ti faccio sapere.

g non è il prodotto vettoriale dei versori r, i? arccos(g)=angolo(r,i)? volevi dire g=1?

Vista dalla Terra, la Luna occupa mezzo grado di campo visivo: quindi g è sempre 1 circa per ogni punto della superficie; se invece dovesse occupare 90 gradi, g andrebbe da cos(0)=1 (centro) a cos(45)=.71 (bordi), con la luna Luna al centro dell'immagine.

Sì quando ho scritto g = 0 intendevo l'angolo di fase, non il suo coseno, normalmente con g si indica proprio l'angolo. Forse ho capito cosa intendi per prospettiva , per capirci, la sorgente di luce e l'osservatore sono quindi a distanze diverse dalla sfera? Così che theta_i rimane invariato e varia theta_r in funzione della distanza dell'osservatore dalla sfera?

Ho preparato uno schema con Geogebra:



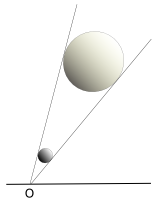
Le rette arancioni rappresentano i raggi solari th_i (paralleli); quelle nere tratteggiate, i raggi th_r che entrano nella camera; C è il foro della camera.

I raggi th_i e th_r necessariamente divergono a mano a mano che la porzione ripresa si allontana dal centro immagine: più l'oggetto è vicino e maggiore sarà quest'angolo (immagine di sx); angolo che diminuisce con la distanza (immagine di dx), arrivando idealmente a zero solo a distanza infinita.

Ottimo, ora ci siamo capiti Io mi stavo riferendo ad un ipotetico fotogoniometro in cui la differenza di posizione è solo una differenza di posizione angolare, e quando cos(g) = 0 theta_i e theta_r coincidono e la funzione di Lommerl-Seeliger vale sempre 0.5 per ogni punto della sfera. Quindi sì, la funzione tiene conto anche della posizione dell'osservatore dalla superficie nella misura in cui cambia theta_r.

Sto cercando di ripetere l`esperimento del messaggio 9077

il mio risultato (preliminare) e` questo:



I falsi colori mappano l`angolo g, ricavato con la formula seguente:

Il modello iniziale e` composto da un piano (suolo lunare) e da un disco riflettente (dovrebbe rappresentare la tuta spaziale, ma per il momento e` semplicemente uno specchio); il cielo e` posto a 1 per convenzione e ho aggiunto l`ombra per far capire la provenienza della luce.

Kamiokande, mi piacerebbe verificare la correttezza del mio modello riproducendolo con Mitsuba: con quest`ultimo programma, e` possibile mappare il valore di g sull`immagine?

Per il momento devo ancora capire bene come applicare la formula di Hapke: pensavo qundi di provare il mio programma con i valori precalcolati da Shevchenko.

La tabella seguente contiene i dati raccolti per l`angolo ph_i= 0; nella prima colonna il valore dell`angolo th_r [0,90,+10]; nelle righe i valori per il corrispondete angolo ph_r [0-180,+10] (sempre uguale quando ph_i= 0).

il grafico (con i dati negativi speculari) ottenuto sommando le righe e normalizzando :

Rispetto al tuo risultato preliminare così a prima vista c'è qualcosa che non mi torna, ma dovrei studiare meglio la questione prima di pronunciarmi. Se ho tempo provo a replicare quanto da te fatto.

Kamiokande, mi piacerebbe verificare la correttezza del mio modello riproducendolo con Mitsuba: con quest`ultimo programma, e` possibile mappare il valore di g sull`immagine?

Dubito che lo possa fare (puoi misurare irradianza, radianza e fluence) ma credo sia possibile scrivere un plug-in per farlo (un integrator ad hoc, oppure più semplicemente un BSDF che invece della riflettanza ritorni g), e non dovrebbe essere nemmeno così complesso da fare ma occorrerebbe comunque del tempo per capire come funziona mitsuba e la sua interfaccia ai plug-in.

Comunque se riesci ad implementare i valori tabulari di Shevchenko possiamo confrontarlo direttamente con un rendering di mitsuba con lo stesso materiale.

Ho fatto una prima simulazione con il Sole a 20 gradi di elevazione e 45 di azimuth (angolo ph_i=70, th_i=45).

La tabella di Sc. corrispondente a i=70:



Luminosita` calcolata (gli angoli non sono interpolati):



Con questa prima prova, la differenza di lum. tra lo specchio e la superficie e` di circa 10 volte: lo scarto e` dovuto al fatto che i raggi riflessi rimbalzano dal terreno con un angolo ph_i piu` vicino a quello della luce solare.

@kamiokande: nell`immagine del messaggio precedente (mappatura angolo g) credo di aver sbagliato i segni dei vettori.

A me, pur avendoci fatto caso moltissime volte, non è mai capitato di vedere le ombre dirigersi in direzioni diverse (anche di molto)
come invece si evincerebbe dalle foto nasa e dal filmato dei due debunkers usa-canaglia....
Giuro che cercherò di riprodurre lo stesso tentativo fatto da loro per appunto verificare se sia vero o meno...
Ma poi cosa dovrei fare?
Dovrei forse mettere online tutte le volte che verifico o che faccio delle prove?
E se non riuscissi a replicare quello che invece i due debunkers avrebbero dimostrato allora che accadrebbe?
Non sarei creduto e sarei tacciato di manipolazioni video o chissà quale altra assurda spiegazione?
Non capisco, non mi è mai capitato di vedere un effetto ombra diverso dal comune...
ps: senza polemica ma personalmente penso che attivissimo sia qui dentro molto più presente e costante di quanto possiamo immaginare.
Che si cloni, che si inventi due o tre personaggi clonati, che li abbia chiamati a svolgere la loro funzione di debunker insiema a lui,
non cambia. Perchè personalmente sono convinto che potrebbe esserlo e questo nessuno potrà mai dimostrarmi del contrario!
Appunto perchè non potranno mai dimostrarlo rimane viva la mia convinzione!
Quindi sarebbe meglio che ti facessi vedere....
....appari o grande illuminato!

Nelle vicinanze del centro immagine, la differenza di angolo ph tra il raggio riflesso dallo specchio (considero il valore dell`angolo prima della riflessione) e il raggio che entra direttamente nella camera dovrebbe essere del doppio del valore dell`angolo tra il piano della camera e il raggio solare: se l`angolo e` 45 gradi, come nella mia simulazione, abbiamo quindi uno scarto di 90 gradi tra ph_i e ph_r (9 posizioni nella tabella di Sc.).

La luminosita riflessa (45 gradi) vale circa 0.4, quella diretta (135 gradi) 0.05.

Ho preparato altri tre grafici:



Le immagini rappresentano una superficie bidimensionale di cento metri di lato sulla quale sono mappati i valori degli angoli th_r (1), ph_r-ph_i (2) e della funzione di Shevchenko (3) f(th_i,th_r,ph_r-ph_i); la camera e` posizionalta al centro (50,50), ad un altezza di 1.2 m; l`angolo th_i e` 70 gradi e quello ph_i 45. I valori degli angoli nelle prime due immagini vanno moltiplicati per 10.

Perdona il ritardo ma non ho avuto molto tempo in questo periodo. Ho scritto un piccolo programma Matlab per fare qualcosa di simile a quanto fatto da te, qui puoi vedere una semisfera appoggiata su un piano con theta_i = 75°, phi_i = 0°, e theta_r = 44°, phi_e = 60°



La telecamera è posizionata correttamente rispetto agli angoli da me scelti. Per il momento la scala dei colori è legata ad una legge di Lambert per entrambi ( L = cos(theta_i ) ). Come vedi se la sfera può sembrare corretta il piano di sicuro non lo è, invece dividendo per cos(theta_i ) il piano risulta corretto, con una colorazione costante, ma la sfera di sicuro è errata. Dopo Pasqua, appena riesco, provo ad implementare l'equazione di trasporto per vedere cosa ottengo.

Rivitalizzo questa discussione :poke:

Ho riscritto il programma usando delle sfere perfettamente riflettenti; in questa immagine la luce è a 45 gradi di elevazione, alle spalle del soggetto inquadrato; la luminosità è calcolata secondo la tabella di Scevchenko.



Questa è una prima prova: per semplicità il materiale è riflettente (la versione "diffusa", più complessa da calcolare, la sto scrivendo in OpenCL) e le geometrie si riducono alla sola sfera; si può comunque notare (salvo errori) come paradossalmente lo sfondo sia meno luminoso del riflesso, nonostante il riflesso sia in controluce.