Analisi anomalie foto Apollo con strumenti matematici

doktorenko ha scritto: Propongo altre ipotesi:

1) dato sbagliato distanza Terra-Luna
2) la luminosita`/atmosfera della Terra la fa apparire leggermente piu` grande
3) variazione di lunghezza focale dovuta alla messa a fuoco

1) La distanza Terra-Luna "corretta" dovrebbe essere 386330 km, come detto nel mio post precedente.
2) Si può verificare analizzando altre foto come l'Earth rise dell'Apollo 8, oppure il blue marble dell'Apollo 17, per vedere se anche in quei casi dove i contorni sono più netti si ha uno scostamento simile.
3) Anche questo è possibile ma non verificabile. Personalmente trovo il discorso della messa a fuoco una bella gatta da pelare per gli astronauti che non avevano il finder sulla Hasselblad, eppure la gran parte delle foto sono praticamente perfette "grazie agli appositi training che gli astronauti avrebbero seguito" (come dicono i debunkers).

Per curiosita` ho provato anche a calcolare lo schiacciamento polare: nell`ipotesi migliore (entrambi i poli visibili dalla Luna) dovrebbe essere di 0.7 pixel circa.

Direi che è fisicamente consistente. La differenza tra il raggio medio della terra ed il raggio polare dovrebbe essere intorno allo 0.2% quindi la Terra è praticamente sferica.

kamiokande ha scritto: 1) La distanza Terra-Luna "corretta" dovrebbe essere 386330 km, come detto nel mio post precedente.

Come e` calcolata? perche` a noi interessa la distanza superficie Luna-centro Terra, e non centro-centro (sono circa 2000km di differenza). Per non equivocare possiamo chiamarla "distanza camera-centro sfera inquadrata".

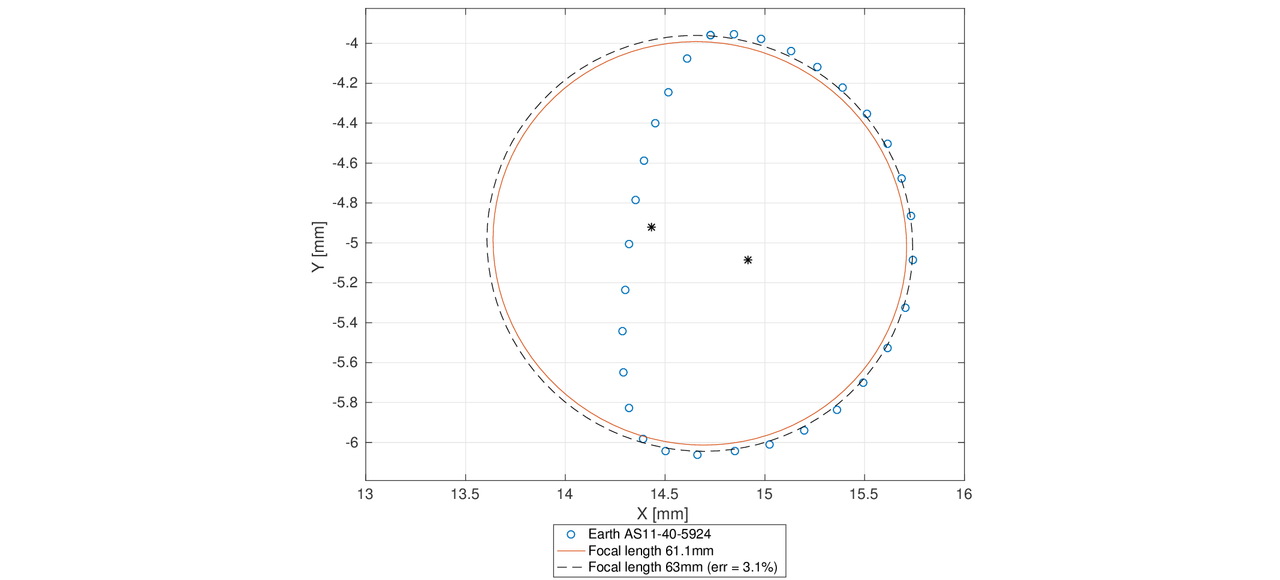
La linea continua rossa è la Terra proiettata sull'immagine con una lunghezza focale di 60mm

Attento perche` la lunghezza focale dovrebbe essere di 61.1 mm e non 60. La tua immagine conferma comunque un leggero scostamento tra i dati e la fotografia, imprecisione che si puo` spiegare forse con pochi mm di messa a fuoco, anche se il soggetto all`infinito dovrebbe essere fotografato usando la lunghezza focale nativa della camera, che e` appunto 61.1 mm; quindi potrebbe essere pure un`immagine fuori fuoco

Per quanto riguarda il contributo dell`atmosfera-luminosita` bisognerebbe scontornare accuratamente la Terra dall`alone circostante; come hai proceduto tu per l`identificazione della sagoma?

Adesso sto cercando di raddrizzare la Terra, proiettando a ritroso la sua immagine su di un piano inclinato di un angolo delta rispetto a quello della pellicola; la Terra cosi` raddrizzata dovrebbe essere perfettamente circolare. Lo scopo dell`operazione e` duplice: verificarne la forma corretta e poter lavorare piu` comodamente sull`immagine, ad esempio per scontornarla piu` accuratamente.

Come e` calcolata?

Non sono sicuro al 100% ma da quel che ho trovato su internet e da quel che si vede usando il programma è la distanza dall'osservatore (in questo caso dalla superficie della Luna nel landing site dell'Apollo 11) al centro dell'oggetto osservato, quindi per questo ho detto che è la distanza corretta.

Per quanto riguarda il contributo dell`atmosfera-luminosita` bisognerebbe scontornare accuratamente la Terra dall`alone circostante; come hai proceduto tu per l`identificazione della sagoma?

Ho usato l'algoritmo automatico di WebPlotDigitizer. Per sicurezza ho definito un contorno manuale dopo aver applicato con Gimp un filtro sharpen alla foto originale per avere un contorno più netto.




La differenza come puoi vedere non è così apprezzabile (c'è un maggiore scostamento dal perimetro ma personalmente mi fido di più della nuvola di punti generati in automatico da WebPlotDgitizer).



Ho corretto la lunghezza focale a 61.1mm ed ora l'errore è del 3%. Ho anche aggiunto i fuochi dell'ellisse proiettato (i marker * neri) per dare una idea dell'eccentricità.

Come ho già detto, considerando tutti i passaggi effettuati , un errore del 3% è più che giustificato (vendendolo ora con una lunghezza focale di 61.1mm mi pare che la differenza sia data solo dall'atmosfera), quindi non vedo il motivo di accanirsi tanto. Credo che abbiamo smentito i Moon Hoaxer che parlano di una Terra troppo piccola nelle foto, questo con somma gioia dei debunkers :baby: .

doktorenko ha scritto:
E io ho pure una formazione classica, ma ho capito il tuo procedimento; con quello speculare (cubo obliquo e piano yz) l`equazione dell`ellisse mi risulta:

Code:

x^2 (cos^2(δ) - sin^2(δ) tan^2(ρ)) - 2 f x tan(δ) tan^2(ρ) + y^2=f^2 sec^2(δ) tan^2(ρ)

Questa sicuramente non è corretta perchè per rho=delta non si annulla il termine a destra, quindi non fornisce una curva passante per l'origine.

Per il momento teniamo per buona l`equazione (2): questa dovrebbe essere la curva parametrica dell`ellisse nella forma Cx+cos(t)*r Cy+sin(r)*r; con Cx,Cy il centro della sfera nell`immagine proiettata, e non il centro dell`ellisse.

Credo che bisognerebbe stabilire un po' di rigore matematico. Il tuo sforzo doktorenko è encomiabile, però i risultati sono approssimazioni, per esempio l'equazione 2) non è un'ellisse, è una quartica, che in effetti per valori non troppo grandi di rho fornisce una buona approssimazione dell'ellisse che cerchiamo. Al crescere dell'angolo rho le cose cambiano:

qui ho usato rho=45°, quindi per una sfera che occupa praticamente tutta l'inquadratura (sempre spostata di 15° dal centro) si nota un certo sfasamento...



...qui invece con rho=65° si vede una specie di campanella di natale. Detto questo, per i valori di rho che ci interessano può anche andare bene, anche se non capisco l'utilità di continuare a usare un'equazione che non fornisce indicazioni dirette nè sul centro nè sugli assi della conica, avendo a disposizione le equazioni parametriche standard, non approssimate per di più.

A dire il vero è tutto il procedimento che non condivido: che senso ha perdere tanto tempo a ricavare delle equazioni il più possibile esatte quando poi le usiamo per un confronto a occhio con degli scorrevoli di geogebra? Per me i procedimenti possibili sono 2:

-quello usato da kamiokande, con l'ausilio di software specifici e senza sbattersi più di tanto a calcolare proiezioni e sezioni;

-quello fai-da-te usando geogebra che vado a illustrare adesso.

Visto che l'equazione implicita della proiezione della sfera ce l'abbiamo, se vogliamo sfruttarla a dovere ecco un metodo. Partiamo dalla foto dimensionata e centrata giusta, cosa di cui io non dispongo (a questo proposito: non vedo più le foto di doktorenko, le mie e quelle di kamiokande invece le vedo), e usiamo lo strumento "conica per 5 punti" di geogebra. Approssimazione per approssimazione, facciamo questa e poi usiamo solo equazioni esatte. Allora il risultato sarà l'equazione implicita di una ellisse, da questa si ricava immediatamente il centro (e quindi R, lo scostamento in mm dal centro dell'immagine) e l'angolo alfa. Ruotiamo l'ellisse in modo da metterci nella comoda situazione alfa=0, e dividiamo tutti i termini per il coefficiente di y^2. Questo serve per fissare l'equazione implicita fra le infinite che differiscono per una costante moltiplicativa.

Ora prendiamo l'equazione implicita 3) del commento #8123 e anche in questa dividiamo tutti i termini per il coefficiente di y^2, cioè (1+R^2/F^2). Adesso uguagliando i coefficienti dei termini x^2, x, 1 (termine noto) delle due equazioni implicite abbiamo a disposizione tre equazioni nelle due incognite r e F e possiamo o cercare di risolverle direttamente, ma non è detto che il sistema abbia soluzioni esatte, ricordiamoci che abbiamo usato delle approssimazioni, oppure tracciare le tre curve corrispondenti e cercare una (o più) intersezioni comuni a tutte e tre, se non ci fossero possiamo facilmente stimare i punti che più ci vanno vicini e leggere nel piano i relativi valori approssimati di r e F. Altrimenti volendo essere ancora più rigorosi si può cercare una soluzione approssimata "esatta" nel senso dei minimi quadrati, ma non mi sembra il caso.

Fatto ciò possiamo controllare se i valori trovati per la focale e il raggio terrestre apparente sono consistenti con i dati reali. Però a questo punto io tenderei a fidarmi del lavoro di kamiokande: se la differenza tra focale teorica e focale calcolata è nell'ordine dei 2 mm direi che è ampiamente dentro la tolleranza e può essere spiegata con la somma di diversi fattori (messa a fuoco, dilatazione termica, ecc.) del tutto normali.

FranZeta ha scritto:

doktorenko ha scritto:
... cubo obliquo e piano yz, l`equazione dell`ellisse mi risulta:

Code:

x^2 (cos^2(δ) - sin^2(δ) tan^2(ρ)) - 2 f x tan(δ) tan^2(ρ) + y^2=f^2 sec^2(δ) tan^2(ρ)

Questa sicuramente non è corretta perchè per rho=delta non si annulla il termine a destra, quindi non fornisce una curva passante per l'origine.

Si` pero` nella mia costruzione (messaggio #8111) l`ellisse risultante e` sempre centrale (anche se non posizionata perfettamente al centro), perche` l`asse del cono obliquo passa per (0,0,0): ho dimenticato di traslarla.

Credo che bisognerebbe stabilire un po' di rigore matematico.

Ti do ragione, anzi, fai bene a bacchettarmi! Ho aperto appositamente questa discussione perche` spesso leggevo delle affermazioni tipo: "si vede benissimo che la Terra e` molto piu` piccola!". E io pensavo allora: "se si vede benissimo ad occhio, sara` anche possibile in qualche modo calcolarlo, e avere cosi` una prova inoppugnabile". Pero` nessuno poi faceva questo benedetto conto...

Nel mesaggio #8127 pero` avevo scritto di aver intenzione di alleggerire per un po` la discussione, postando finalmente delle immagini, per interrompere questi infiniti preliminari matematici (che sono pero` doverosi).

Il tuo sforzo doktorenko è encomiabile, però i risultati sono approssimazioni, per esempio l'equazione 2) non è un'ellisse, è una quartica, che in effetti per valori non troppo grandi di rho fornisce una buona approssimazione dell'ellisse che cerchiamo. Al crescere dell'angolo rho le cose cambiano...

Io ho provato con gli stessi angoli, ma a me l`ellisse rimane "in forma". Io uso questa equazione (copio direttamente da Geogebra):

A dire il vero è tutto il procedimento che non condivido: che senso ha perdere tanto tempo a ricavare delle equazioni il più possibile esatte quando poi le usiamo per un confronto a occhio con degli scorrevoli di geogebra? Per me i procedimenti possibili sono 2:

Come ho detto, le ultime analisi che ho inviato erano da considerarsi piu` leggere.

-quello usato da kamiokande, con l'ausilio di software specifici e senza sbattersi più di tanto a calcolare proiezioni e sezioni;
-quello fai-da-te usando geogebra che vado a illustrare adesso.

Adesso sto procedendo in questo modo:

1) raddrizzo l`immagine (come ho scritto sopra), anche se eventualmente questa rotazione potrebbe degradarne la risoluzione
2) calcolo il raggio della circonferenza ottenuta (che dovrebbe essere quasi perfetta) con metodi digitali, magari impostando una soglia di luminosita` che separa la Terra dall`atmosfera, e uso questo raggio come riferimento.

comunque siamo qui apposta, per discutere e per proporre delle soluzioni.

Scusami, se io volessi controllare la mia equazione con la tua del messaggio #8123, come devo scriverla in geogebra, usando la mia convenzione (angolo delta, raggio rho, focale F, ecc.)? potresti riportarla in formato testo, citandola tra i marcatori code? Anche perche` abbiamo visto che le immagini potrebbero sparire, mentre lo scritto no

EDITATO E CORRETTO

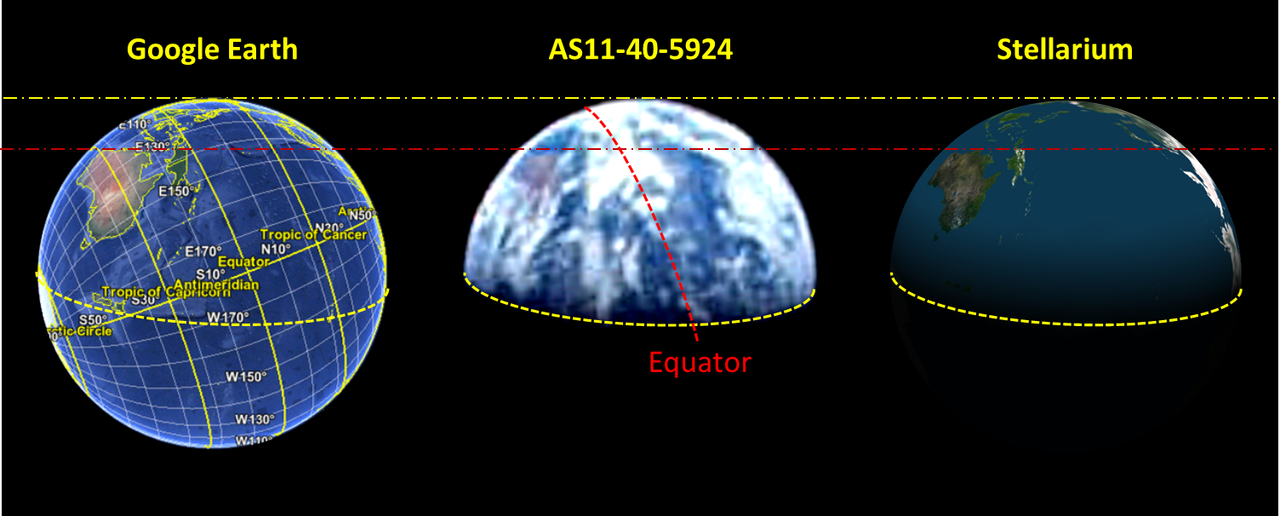
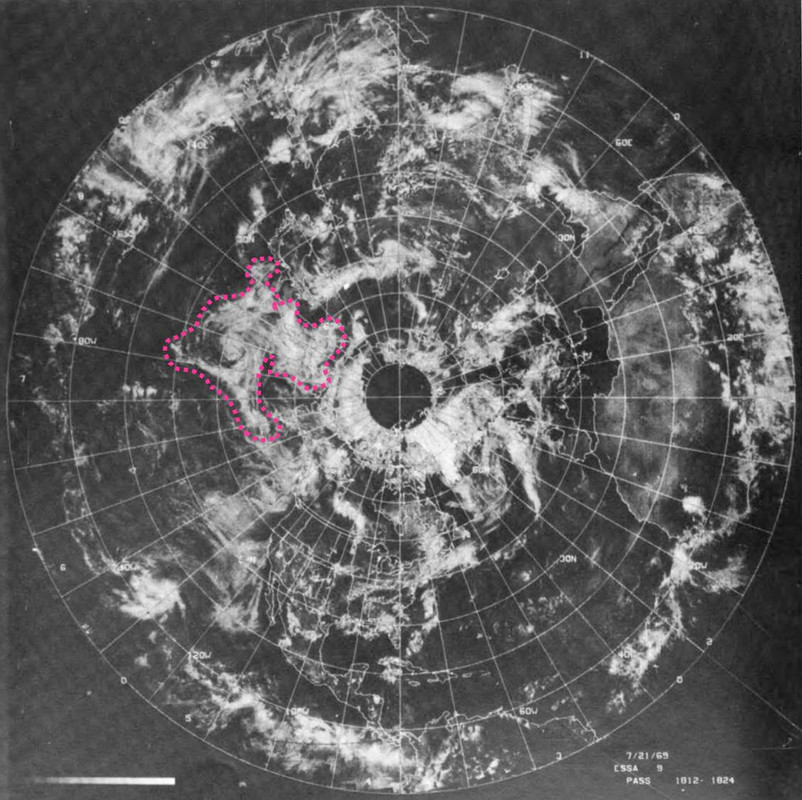
Vado un po' off-topic. Forse ho trovato un'incongruenza riguardo alla foto esaminata AS11-40-5924 che però non riguarda le dimensioni dell'immagine della Terra. Osservando con Stellarium la Terra al 21 luglio del 1969 alle 4:22 UTC (quando sarebbe stata scattata la foto) possiamo verificare la corrispondenza dell'illuminazione tra l'immagine generata dal software e la foto.



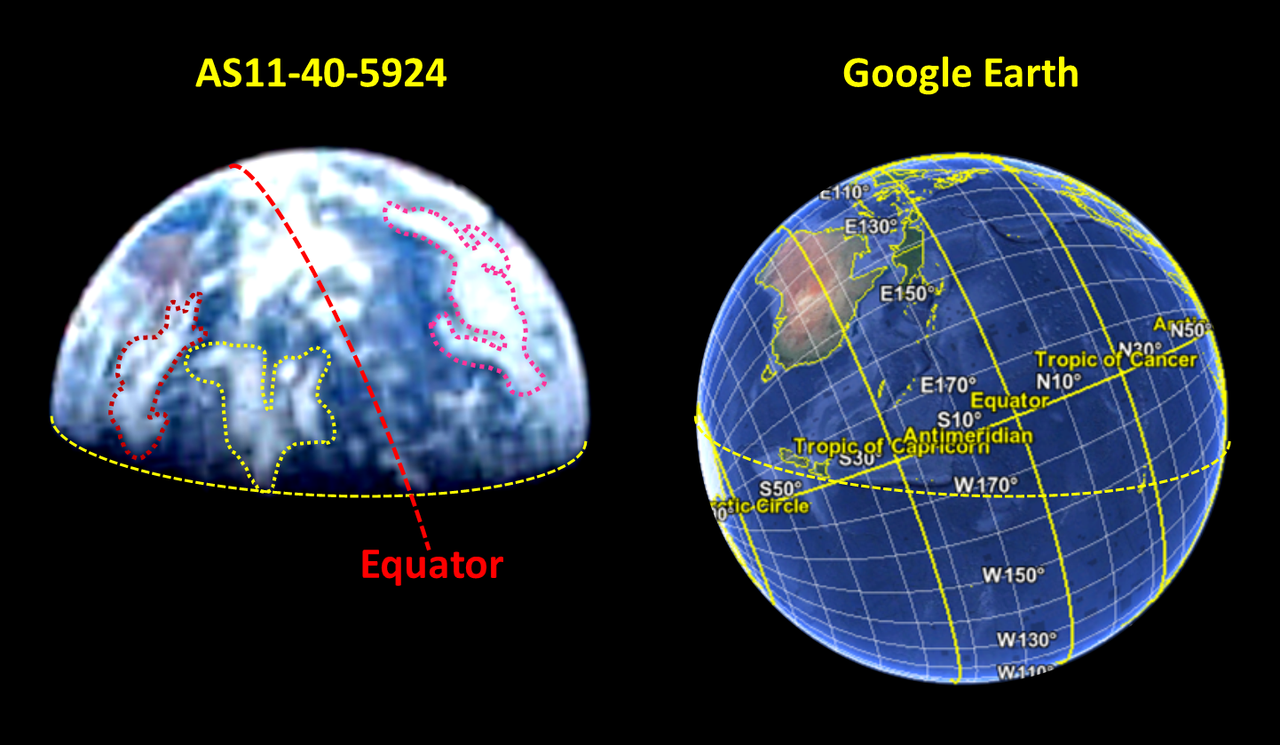
Isolando ed identificando alcune formazioni nuvolose è possibile verificare la data nel quale la foto è stata scattata.



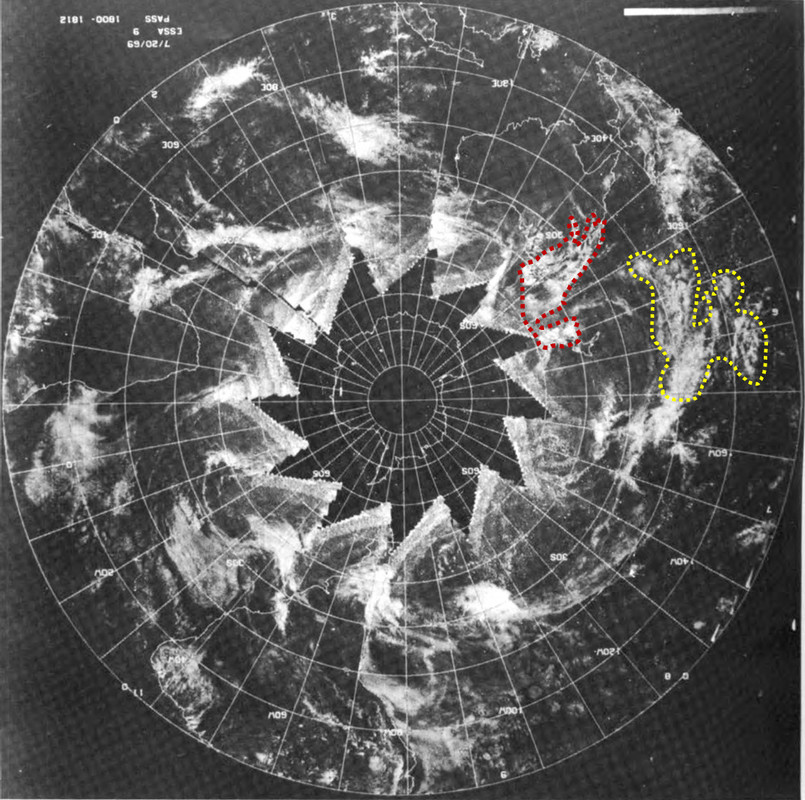
Consultando il documento Key to meteorological records documentation no.5.323 , possiamo vedere, con l'aiuto di Google Earth, che quelle formazioni nuvolose si possono trovare il 20 luglio 1969.

Emisfero Nord - 20 Luglio 1969


Emisfero Sud - 20 Luglio 1969


Emisfero Nord - 21 Luglio 1969


Emisfero Sud - 21 Luglio 1969


Le formazioni nuvolose dell'emisfero Sud non sono presenti il 21 Luglio, mentre la formazione ciclonica nell'emisfero Nord presenta una forma differente. Se la costruzione delle mappe è su base giornaliera è quindi possibile che la foto AS11-40-5924 sia sta scattata non il 21 ma il 20 luglio alle 4:22 UTC, quando la Terra occupava la stessa posizione rispetto al Sole.

Esiste però un incongruenza tra la data riportata sulle mappe ed i passaggi (PASS) che rende l'interpretazione delle mappe non immediata. Ci sono due possibilità:

1) Le mappe sono su base giornaliera dalle 00:00 GMT alle 24:00 GMT di ogni singolo giorno ma i passaggi indicati servono solo a garantire la sovrapposizione tra la fine di una mappa e l'inizio della successiva, nel documento "Key to meteorological records documentation no.5.323" viene specificato che la sovrapposizione viene effettuata nel planisfero tra i 60°E e gli 80°E che il satellite ESSA 9 sorvola intorno alle 10 GMT.

2) Le mappe sono generate dai passaggi indicati ovvero tra le 10:00 GMT del giorno indicato e le 10:00 GMT del giorno successivo, quindi la data indicata sulle mappe perde di significato e metà planisfero è riferito al giorno indicato e metà nel giorno successivo.

Benché io trovi alquanto strano che sia vero il secondo caso, nel caso fosse quello corretto le formazioni nuvolose corrisponderebbero al momento in cui le foto sarebbero state scattate, altrimenti occorrerebbe retrodatare di un giorno tutte le foto in cui compare la Terra con pesanti ripercussioni sui dati riportati dalla NASA. Devo verificare con altre immagini satellitari quale delle due sia corretto. Esistono comunque altre incongruenze legate alla foto analizzata che meritato di essere valutate.

AGGIORNAMENTO

Ho verificato che effettivamente il secondo caso è quello corretto quindi le foto della Terra sono fisicamente coerenti nel momento in cui ufficialmente sono state scattate. Mi scuso per la svista.

doktorenko ha scritto: Nel mesaggio #8127 pero` avevo scritto di aver intenzione di alleggerire per un po` la discussione, postando finalmente delle immagini, per interrompere questi infiniti preliminari matematici (che sono pero` doverosi).

Sono d'accordo, e anche se non lo fossi il thread lo hai aperto tu e sei libero di impostarlo come preferisci, solo che è più forte di me, le imprecisioni matematiche (anche e soprattutto le mie, vedi il mio primo commento) mi causano prurito e altri sintomi fastidiosi finchè non vengono estirpate...

Io ho provato con gli stessi angoli, ma a me l`ellisse rimane "in forma". Io uso questa equazione (copio direttamente da Geogebra):

Code:

F = 61.1 d=tan(δ) F h=F sec(δ) r(t)= h sin(ρ) / sin(ρ - acos(sin(δ) cos(t - α))) Curva[d cos(α) + cos(t) r(t), d sin(α) + sin(t) r(t), t, 0, 2π]

Io mi riferivo alla prima equazione che avevi postato, che in effetti riguardando sarebbe la 1) del commento #8096. Che però non è equivalente a questa qui sopra, come dici alla fine dello stesso commento. Comunque anche quest'ultima equazione è una quartica, solo che la cosa diventa evidente al crescere di delta invece che di rho come in quell'altra:


Qui ho usato delta=65° e rho=15°

Scusami, se io volessi controllare la mia equazione con la tua del messaggio #8123, come devo scriverla in geogebra, usando la mia convenzione (angolo delta, raggio rho, focale F, ecc.)? potresti riportarla in formato testo, citandola tra i marcatori code? Anche perche` abbiamo visto che le immagini potrebbero sparire, mentre lo scritto no

Questa è l'equazione implicita, per controllare che un'equazione parametrica definisca gli stessi punti devi sostituire x(t) e y(t) alle x,y dell'equazione e verificare che risulti 0=0. Nel tuo caso dovresti porre alfa=180° per un'eventuale coincidenza, ma il grafico qui sopra ci dice già che non potrà esserci.

@kamiokande

Interessante la tua analisi delle nuvole, direi che ammettendo che sia corretta dimostrerebbe due cose:
-l'immagine è un fotomontaggio
-l'immagine della terra è una vera immagine di un satellite (speriamo che non mi legga un tarrapiattista), mi sembra troppo complicato realizzare un modello con riproduzione fedele delle nuvole a una data prefissata (inoltre a quel punto potevano scegliere la data giusta...).
Questo significherebbe anche che l'immagine della terra è in realtà in origine digitale, mi sembra improbabile che abbiano fatto foto su pellicola con un satellite e poi recuperato il rullino....

@ Franzeta

Ho seguito il procedimento usato da un certo Paul White, che usa questo metodo per dimostrare che la Terra nelle foto delle missioni Apollo è autentica e di conseguenze che le foto sono autentiche. Ho però sbagliato ad interpretare le foto del satellite, leggendo il documento mi sono reso conto che sono fatte con un unico satellite (ESSA 9) che sorvola la Terra tra le 12 e le 13 volte per fotografare tutta la Terra, quindi quello che io ho creduto essere l'ora di assemblaggio dell'immagine, sono invece i passaggi (PASS), ricontrollo le mie affermazioni e poi edito il mio post con le considerazioni corrette.

Ho effettivamente verificato che la maggior parte delle foto della Terra nelle missioni Apollo 11 sono effettivamente state scattate alla data indicata dalla NASA.
Ho editato il post aggiungendo la suddetta conclusione.

Ci sono però altre possibili incongruenze che voglio verificare, prima però controllerò tre volte i dati prima di postare qualcosa.

@kamiokande
Non ti devi preoccupare di andare fuori tema finche` la discussione rimane sul piano dell`analisi geometrico-matematica, piuttosto che quello dell`impressione soggettiva.
E` interessante lo studio delle formazioni nuvolose, tra le altre cose sto cercando di separare (previo raddrizzamento) i vari elementi dell`immagine (mare, atmosfera, terra, nuvole) e riproiettarli su di una sfera, per analizzarli meglio; magari anche per valutare se l`illuminazione e` corretta.

Ritorniamo ora all`analisi che abbiamo iniziato, vi spiego la procedura di raddrizzamento; indichiamo con:

La teoria e` che tutti i piani perpendicolari alla retta congiungente il centro della sfera reale e il punto O contengono l`immagine bidimensionale non distorta della sfera; una prima procedura allora potrebbe essere questa:

1) centriamo sul piano p l`immagine da elaborare, ponendo la crocetta grande sul punto O_1 2) stimiamo il centro C della sfera da raddrizzare: 3) conduciamo una retta r da C a O: 4) sulla retta r, a distanza 2OC da C (OC da O), sul punto C1, costruiamo un piano p1 perpendicolare a r; 5) trasformiamo i punti 2d I[r,c] dell`immagine in punti 3d: 6) calcoliamo il parametro t per il piano p1: 7) proiettiamo i punti P sul piano p1: la matrice di punti P1, nel piano bidimensionale p1, rappresentano l`immagine della Terra raddrizzata

Il problema adesso e` rendere bidimensionale il pianop1, ma forse sarebbe meglio allora, in maniera speculare, distorcere il piano p, che e` gia` bidimensionale. Si potrebbe semplificare anche orientando l`immagine preventivamente, facendo coincidere il centro della Terra con uno degli assi x y passanti per il centro della foto, ma vorrei evitare le rotazioni, perche` potrebbero portare ad una perdita di informazione.

Seconda procedura:

1)calcolo gli angoli di inclinazione del piano p1, rispetto al piano xz del sensore: 2)calcolo conseguentemente due vettori direzione, che trasformano un movimento bidimensionale in uno corrispondente sul piano p1, relativo ad un punto sullo stesso: 2b)cioe` per scostarmi dal punto C1 di r righe e c colonne, e sapere la coordinata 3d corrispondente sul piano p1, devo moltiplicare r e c per u e v: 3) per conoscere il punto P_r_c corrispondente sul piano p, moltiplico il punto P1_r_c su p1 per il parametro t: 4) disegno l`immagine RGB bidimensionale raddrizzata usando i nuovi indici calcolati come sopra:

Bisogna pero` fare attenzione a questi aspetti:
1) la stima preventiva del centro della Terra sull`immagine
2) differenza tra lunghezza focale dichiarata e effettiva
3) la distorsione introdotta porta ad una perdita/degrado dell`informazione

La 1 e` marginale perche` dovrebbe influire poco sul risultato finale (pochi pixel di differenza corrispondono a frazioni minime di angolo), mentre la 2 e` piu` importante perche` pochi millimetri di lunghezza focale possono variare molto di piu` lo scostamento angolare calcolato, e quindi la deformazione dell`immagine; la 3 e` da valutare

@ doktorenko

Io ho calcolato che la dimensione della Terra non distorta (considerando anche la parte non visibile) con una focale di 61.1mm dovrebbe essere di 2.016mm, considerando che la distanza tra i marker è di 10mm. Il semiasse maggiore della Terra distorta dovrebbe essere di 2.0799mm, quindi la differenza è di circa 3.1% e non so quanto sia apprezzabile e considerando gli errori che si commettono sempre.

Si ha all'incirca la stessa differenza se la lunghezza focale fosse di 63mm.

La deformazione non si nota perche` non c`e` la comparazione, ma l`allungamento nell`originale e` evidente: ovvero la mia, a confronto, e` abbastanza schiacciata. Resta adesso da stabilire in che misura la mezza Terra "raddrizzata" corrisponda ad una porzione di cerchio perfetto.

P.s.
Ho pensato di togliere l`immagine elaborata perche` messa cosi` non e` di molta utilita`.

Ho provato a usare la procedura di "raddrizzamento" su di un`immagine prodotta a partire da un modello tridimensionale:

Poi, con due funzioni del pacchetto scientifico per Python, ho estratto il contorno e stimato il raggio e il centro della circonferenza.

Questo e` il risultato finale:


Metto i passaggi per risalire alle dimensioni reali:
L`imprecisione e` di circa il 6 per mille; la procedura dovrebbe quindi funzionare "teoricamente", cioe` conoscendo con precisione la lunghezza focale dello scatto e avendo dei bordi ben definiti: due dati che nella situazione reale dobbiamo purtroppo stimare in qualche modo.

Tenuto conto di queste difficolta` io direi di passare a trattare altre eventuali anomalie "calcolabili" nelle foto Nasa; ad esempio se e` possibile stimare la curvatura lunare (tentativo che avevo gia` fatto nella discussione precedente).

P.S.

Ho trovato un errore concettuale nel calcolo del diametro reale: non dobbiamo piu` tener conto della distanza della sfera, ma del cerchio di diametro angolare asin(R/D) visibile della stessa; la nuova distanza a cui fare riferimento dovrebbe allora diventare:

E il raggio visibile:

Immagine della Terra presa dalla foto AS11-40-5924, riproiettata su di un piano posto a distanza F1*2 (cioe` raddrizzata e ingrandita x2), centrata manualmente, il raggio indicato corrisponde a quello terrestre (circa 6378 km, 156,5 px):



Per me l`eccedenza potrebbe essere benissimo atmosfera e/o luminosita` "sparata" (1px = 40km).

La procedura per verificare la corretta curvatura del terreno nelle foto Apollo consiste nel costruire un modello tridimensionale partendo dai dati digitali delle sonde (ricostruizione profilo orografico) e dagli scatti da analizzare (orientamento e posizione camera), mappare quindi la superficie risultante su di una sfera/ellissoide/"lunoide", e confrontare le altezze dei rilievi.

Si potrebbe obiettare che la Nasa ha modellato l`ambientazione tenendo conto della curvatura: se l`ha fatto in scala 1:1 per me e` fantascientifico (ma anche senza curvatura); oppure che i dati delle sonde sono stati taroccati successivamente per combaciare con le foto: se e cosi` questi stessi dati sono la prova che cerchiamo -naturalmente potendo confrontarli con quelli di una sonda "neutrale".

Iniziamo ora da un modello "base", successivamente cerchiamo di rifinirlo il piu` possibile, visto che le differenze potrebbero essere i pochi centesimi di millimetro sulla pellicola (1 mm circa 75 px).

In questo caso semplificato, se:

i punti della (Px,Py,Pz) della calotta sferica saranno:

La calotta e` costruita per avere il punto piu` alto = livello 0 = posizione camera.

Fin qua non dovrebbero esserci problemi, se pero` aggiungiamo il dato dell` altezza h, e` sufficiente porre:

e lasciare invariato il resto? si introduce una approsimazione? se si`, e` trascurabile? perche` un altopiano dovrebbe avere una superficie maggiore rispetto allo stesso terreno, , sotteso allo stesso angolo, a livello del mare.

Dovrei capire come eventualmente compensare per le varie altezze, se e` proprio necessario o la differenza, per i rilievi in questione, e` praticamente irrilevante, o se i dati gia` ne tengono conto, o altro.

p.s.

Ho fatto alcuni conti e il risultato mi sembra interessante: un ipotetico altopiano che corresse lungo tutto l`equatore lunare svettando di 1 km ( R + d dal centro; d = 1 km), avrebbe un`estensione maggiore di circa 6.28 km rispetto allo stesso rilievo posto pero` a livello 0 (R dal centro); questo perche`, piuttosto contro-intuitivamente, la differenza non e` correlata con la dimensione iniziale, 2 pi * R, ma semplicemente vale 2 * pi * d: nell`esempio 1 km * 2 pi; questo per un arco di 360 gradi: ma noi trattiamo altezze e estensioni angolari minori -centinaia di metri di dislivello e decimi di grado- quindi potrebbero esserci approssimazioni nell`ordine del metro. Per il momento lascio quindi in sospeso un eventuale aggiustamento dei dati, ma mi piacerebbe comunque approfondire la questione.

doktorenko ha scritto: La procedura per verificare la corretta curvatura del terreno nelle foto Apollo consiste nel costruire un modello tridimensionale partendo dai dati digitali delle sonde (ricostruizione profilo orografico) e dagli scatti da analizzare (orientamento e posizione camera), mappare quindi la superficie risultante su di una sfera/ellissoide/"lunoide", e confrontare le altezze dei rilievi.
...

Code:

1) Luna = sfera di raggio R 2) nessun rilievo 3) corrispondenza esatta (a parte la scala) tra superficie mappata e quella lunare

In questo caso semplificato, se:

Code:

h(dx-cx,dy-cy) = dato altimetrico mappato cx,cy = posizione della camera dx,dy = distanza

i punti della (Px,Py,Pz) della calotta sferica saranno:

Code:

R=raggio x=dx-cx y=dy-cy theta=x/R phi=y/R Px= -sin(theta) * R Py = cos(theta) * sin(phi) * R Pz = cos(theta) * cos(phi) * R - R

La calotta e` costruita per avere il punto piu` alto = livello 0 = posizione camera.

Fin qua non dovrebbero esserci problemi, se pero` aggiungiamo il dato dell` altezza h, e` sufficiente porre:

Code:

h(dx-cx,dy-cy)=altezza terreno R=Raggio+h

e lasciare invariato il resto? si introduce una approsimazione? se si`, e` trascurabile?

Io partirei posizionando la fotocamera nel punto (u,v)=(0,0) (quando si usano coordinate sulla sfera è meglio usare un altro nome, tenendo x,y,z per le coordinate della sfera, cioè le coordinate ortogonali dello spazio tridimensionale), a questo punto (u,v) sono precisamente le due distanze di un generico punto e si può costruire la calotta ponendo:
u è orientata nella direzione dei meridiani e v in quella dei paralleli, in sostanza u è la direzione verso cui è puntata la fotocamera e v la direzione ortogonale destra-sinistra. In questo modo la fotocamera si trova nel punto Eviterei anche con la massima cura di usare dx e dy come variabili dato che in geometria differenziale (e questa vorrebbe essere geometria differenziale) hanno un preciso significato e usarle in una accezione diversa può generare non poca confusione.

MA, detto questo, usare le foto lunari per un lavoro del genere mi sembra del tutto fuori luogo, valutare la curvatura lunare sulla base delle foto nel modo sopra esposto è impossibile, l'unica possibilità è cercare di stimare la distanza o la leggerissima curvatura dell'orizzonte, ma anche in questo caso dubito che si riesca ad arrivare in pratica a qualcosa di significativo. Cercare di stabilire l'eventuale maggiore area di un altopiano lunare rispetto al livello "0" sulla base delle foto è però certamente impossibile.

piuttosto contro-intuitivamente, la differenza non e` correlata con la dimensione iniziale, 2 pi * R, ma semplicemente vale 2 * pi * d: nell`esempio 1 km * 2 pi

La differenza è ovviamente 2*pi*(R+d)-2*pi*R=2*pi*d quindi, come suggerisce il termine stesso, è correlata alla differenza fra i due raggi e non solo al raggio iniziale, non mi pare sia controintuitivo. Ma la differenza nel caso delle foto lunari è sicuramente del tutto impossibile da valutare nemmeno con mezzi molto più sofisticati di quelli usati qui, anche in caso di superficie perfettamente liscia sarebbe di circa un metro sui 2 km di distanza dell'orizzonte (con la fotocamera a 1,20 m di altezza), figuriamoci cosa possiamo concludere nel caso reale in cui sono presenti rilievi di ogni forma e dimensione.

Credo che l'unica possibilità sarebbe stata, nel caso di foto scattate in una zona particolarmente piana, cercare di stimare se l'orizzonte si trovasse ai 2 km della superficie lunare o ai 4 km della superficie terrestre, ma per i motivi già detti non credo che questa verifica sia fattibile in pratica.

FranZeta ha scritto:
La differenza è ovviamente 2*pi*(R+d)-2*pi*R=2*pi*d quindi, come suggerisce il termine stesso, è correlata alla differenza fra i due raggi e non solo al raggio iniziale, non mi pare sia controintuitivo. Ma la differenza nel caso delle foto lunari è sicuramente del tutto impossibile da valutare nemmeno con mezzi molto più sofisticati di quelli usati qui, anche in caso di superficie perfettamente liscia sarebbe di circa un metro sui 2 km di distanza dell'orizzonte (con la fotocamera a 1,20 m di altezza), figuriamoci cosa possiamo concludere nel caso reale in cui sono presenti rilievi di ogni forma e dimensione.

Anch`io sono arrivato a concludere che comunque si tratta di una differenza di estensione nell`ordine del metro, e quindi praticamente impercettibile, ma non pensavo di usare questa eventuale discrepanza come prova; piuttosto il mio dubbio su come trattare i dati altimetrici era questo:

D) due pianure, aventi la stessa estensione angolare (longitudinale e latitudinale), poste pero` ad altezze diverse, sono mappate con lo stesso numero di righe e colonne di dati?

Io direi di si`: quindi, per la trasformazione delle coordinateu,v -> theta, phi bisogna dividere per il raggio standard R; per calcolare invece il punto x,y,z, si deve moltiplicare per il raggio effettivo (in quel determinato luogo) R+h. (come risulta anche dalle tue formule)

Cioe`: stessa estensione angolare in unita`/pixel , ma diversa estensione finale proiettata in metri.

Credo che l'unica possibilità sarebbe stata, nel caso di foto scattate in una zona particolarmente piana, cercare di stimare se l'orizzonte si trovasse ai 2 km della superficie lunare o ai 4 km della superficie terrestre, ma per i motivi già detti non credo che questa verifica sia fattibile in pratica.

Qui non siamo piu` d`accordo: perche` per valutare se una zona e` particolarmente piana dobbiamo necessariamente affidarci ai dati altimetrici; ma non basta: anche ricostruire la linea di orizzonte dalle sole fotografie mi sembra impossibile, non conoscendo con precisione l`orientamento della camera, che invece credo possa essere calcolato incrociando i dati altimetrici e fotografici.

Alcuni conti:

Quindi in una fotografia Apollo 61mm di una zona pianeggiante lunare, con la macchina posta a 1.7m di altezza, l`orizzonte reale dovrebbe giacere 0.08 gradi sotto quello astronomico; ossia, se la camera e` posta a piombo su di un cavalletto: 6 px sotto il centro dell`immagine.

In un ambiente terrestre i conti diventano:

La differenza dovrebbe essere di circa 3 px; pero` potendo fare gli stessi conti con rilievi piu` distanti si dovrebbero trovare differenze maggiori.

doktorenko ha scritto:
D) due pianure, aventi la stessa estensione angolare (longitudinale e latitudinale), poste pero` ad altezze diverse, sono mappate con lo stesso numero di righe e colonne di dati?

E chi lo sa, dipende da come sono stati rilevati i dati dalle sonde, se a intervalli regolari di tempo (quindi di angoli) o di spazio (di metri sulla superficie). Le differenze sarebbero in ogni caso minime. Quello che però è certo è che tutti questi dati provengono da agenzie spaziali, quindi potrebbero essere manipolati in partenza, mi sembra inutile domandarsi se sono organizzati in una matrice 4000x4000 o 4002x4002.

La differenza dovrebbe essere di circa 3 px; pero` potendo fare gli stessi conti con rilievi piu` distanti si dovrebbero trovare differenze maggiori.

Direi che 3 pixel su 4000 sono una precisione che nemmeno se avessero fatto rilevazioni con teodolite e asta graduata potrebbe essere raggiunta. In ogni caso prima di fare ogni tipo di valutazione in questo senso bisognerebbe scegliere le foto da cui si vuole partire, in modo da poter stabilire subito se ha senso o no imbarcarsi in queste considerazioni. In sostanza, secondo me prima di imbastire modelli matematici e relative formule sarebbe opportuno chiarire bene quale dovrebbe essere il loro scopo in relazione al materiale a disposizione.

FranZeta ha scritto:
Direi che 3 pixel su 4000 sono una precisione che nemmeno se avessero fatto rilevazioni con teodolite e asta graduata potrebbe essere raggiunta. In ogni caso prima di fare ogni tipo di valutazione in questo senso bisognerebbe scegliere le foto da cui si vuole partire, in modo da poter stabilire subito se ha senso o no imbarcarsi in queste considerazioni.

Proviamo a fare qualche conto, vienimi in aiuto perche` non mi intendo molto di ottica: con un obiettivo da 60 mm di diametro ( www.hq.nasa.gov/alsj/Biogon5.6_60mm_ZEISS.pdf ), Il potere risolutivo angolare, espresso in secondi di arco, dovrebbe essere:

Un pixel invece sottende un angolo di:

Che e` circa un terzo. L`immagine quindi dovrebbe essere sovra-campionata rispetto alla proporzione canonica 2 a 1; anche se forse i conti bisognerebbe farli sulle caratteristiche della pellicola, e non sulla successiva digitalizzazione. Non so allora se in questo caso (campionamento di un campionamento) la proporzione giusta dovrebbe essere 4 a 1, o comunque superiore a quella consueta.

A parte queste considerazioni, la minima differenza in pixel discernibile dovrebbe quindi essere non inferiore a 3 ?

In sostanza, secondo me prima di imbastire modelli matematici e relative formule sarebbe opportuno chiarire bene quale dovrebbe essere il loro scopo in relazione al materiale a disposizione.

Io intendevo partire analizzando la foto che gia` avevo ricostruito nella discussione precedente (A14-9486). Facciamo altri conti veloci:

Devo pero` ricontrollarli perche` non sono sicuro della loro correttezza.

Io penso poi che non si debba confrontare la caduta lunare con quella terrestre, ma con la curvatura nulla: perche` l`ipotesi di una ricostruzione 1:1 di decine di km quadrati di paesaggio lunare sulla Terra la scarto.

Allego un`immagine di una mia ricostruzione tridimensionale ottenuta dai dati della sonda LRO, con la linea di orizzonte teorica terrestre (piu` alta):



Inizio da questa immagine perche` ho gia` i dati della posizione/orientamento della camera, ma ci sono foto con rilievi molto piu` lontani, ad esempio quelle di Apollo 15:



(distanza rilievo 16 km; questa ambientazione fotografica e` interessante perche` e` stata analizzata da un russo, che vi riscontra anomalie nella parallasse- vedi discussione precedente)

Io procederei in due fasi (accenno solo, dopo possiamo approfondire):

1) orientamento/posizionamento della camera usando oggetti/rilievi vicini
2) calcolo della caduta dei rilievi lontani

doktorenko ha scritto:
Proviamo a fare qualche conto, vienimi in aiuto perche` non mi intendo molto di ottica: con un obiettivo da 60 mm di diametro ( www.hq.nasa.gov/alsj/Biogon5.6_60mm_ZEISS.pdf ), Il potere risolutivo angolare, espresso in secondi di arco, dovrebbe essere:

Code:

a = (135/D) = (135/60) = 2.25"

Un pixel invece sottende un angolo di:

Code:

f = 61.1 mm, 4600 px a = 1/4600 * 3600 = 0.78"

Che e` circa un terzo. L`immagine quindi dovrebbe essere sovra-campionata rispetto alla proporzione canonica 2 a 1; anche se forse i conti bisognerebbe farli sulle caratteristiche della pellicola, e non sulla successiva digitalizzazione. Non so allora se in questo caso (campionamento di un campionamento) la proporzione giusta dovrebbe essere 4 a 1, o comunque superiore a quella consueta.

A me risulta che un pixel, nella zona centrale dell'immagine, corrisponda a Ho usato la risoluzione verticale (o orizzontale, è uguale) perchè è più appropriata di quella diagonale trattandosi di pixel, inoltre è proprio quella che ti interessa. Sulla risoluzione dell'ottica analogica non so dirti, sono un matematico non un fotografo, di sicuro però è almeno un ordine di grandezza superiore a un'ottima campionatura digitale, direi quindi che i conti tornano (tenendo per buona la risoluzione di 2.25" questa corrisponderebbe a un'immagine digitale da 20 GB!). Non capisco cosa intendi con sovracampionamento, ha senso solo fra immagini digitali, fra analogico e digitale il sovracampionamento direi che è impossibile a livello pratico, bisogna anche tenere presente che il campionamento è fatto su una stampa fotografica, non sul negativo, quindi siamo sempre ben lontani dal limite della risoluzione analogica.

Aggiungo anche che per me questa della risoluzione è un'ulteriore complicazione inessenziale: prendiamo per buona la risoluzione digitale delle foto a disposizione dato che i negativi originali non ce li abbiamo, e se non ricordo male alcuni se li sono pure persi.

Io penso poi che non si debba confrontare la caduta lunare con quella terrestre, ma con la curvatura nulla: perche` l`ipotesi di una ricostruzione 1:1 di decine di km quadrati di paesaggio lunare sulla Terra la scarto.

Quella che chiami curvatura nulla in realtà è un'altra cosa, l'orizzonte astronomico è una linea immaginaria, in caso di curvatura nulla l'orizzonte esisterebbe e si troverebbe comunque sotto all'orizzonte astronomico. Se l'orizzonte fosse un fondale di scena avrebbero potuto farlo simulando un qualsiasi orizzonte desiderato, se mai possiamo discutere della bontà della simulazione ma confrontarlo con un inesistente orizzonte astronomico non ha senso. Non solo, come si vede dalla linea rossa che hai aggiunto alla tua immagine basta che la fotocamera sia leggermente fuori bolla, cosa che è praticamente certa nelle foto reali, per annullare ogni considerazione, dato che non c'è modo per risalire al reale orientamento della camera rispetto alla verticale con la precisione necessaria (se ci fosse non esisterebbero i teodoliti per i rilevamenti di precisione, basterebbe una normale macchina fotografica e un software).

C'è anche da aggiungere che esisterebbe pure l'ipotesi inversa di quella che scarti tu: cioè che abbiano ricostruito sulla luna decine di km di paesaggio terrestre, ovviamente non materialmente ma modificando ad arte i dati delle sonde.

Per quanto riguarda la foto A14-9486 che intendi usare nell'analisi mi aspettavo di meglio, è controluce e di qualità molto più scarsa rispetto a quelle di A11 che avevi linkato all'inizio del thread. Nutro anche forti dubbi che il rilievo che si vede sia a 3200 m, si vede una roccia sopra l'angolo in alto a destra del LEM che, se queste fossero le distanze, dovrebbe avere dimensioni colossali, giusto per fare un esempio. L'unica cosa degna di approfondimento che noto nell'immagine è l'ombra del LEM, incoerente con le altre, per giustificarla si dovrebbe ipotizzare una forte inclinazione del terreno alla sua destra. Questa verifica mi sembra fattibile, se si dispone di una buona ricostruzione tridimensionale del sito, mentre sicuramente quella della "caduta dell'orizzonte" non lo può essere.

FranZeta ha scritto: A me risulta che un pixel, nella zona centrale dell'immagine, corrisponda a

Code:

atan(tan(47°)/2000)=1'50.6"

Scusa, ma non dovrebbe esserci 47°/2 tra parentesi? Il mio conto e sbagliato clamorosamente perche` il risultato e` in radianti e non in gradi, quello giusto dovrebbe essere quindi:

Ho usato la risoluzione verticale (o orizzontale, è uguale) perchè è più appropriata di quella diagonale trattandosi di pixel, inoltre è proprio quella che ti interessa.

Anch`io uso la risoluzione orizzontale e la lunghezza focale in px:

Non capisco cosa intendi con sovracampionamento, ha senso solo fra immagini digitali, fra analogico e digitale il sovracampionamento direi che è impossibile a livello pratico, bisogna anche tenere presente che il campionamento è fatto su una stampa fotografica, non sul negativo, quindi siamo sempre ben lontani dal limite della risoluzione analogica.

Credo che le scansioni siano delle diapositive originali, e non di stampe.

Quella che chiami curvatura nulla in realtà è un'altra cosa, l'orizzonte astronomico è una linea immaginaria, in caso di curvatura nulla l'orizzonte esisterebbe e si troverebbe comunque sotto all'orizzonte astronomico. Se l'orizzonte fosse un fondale di scena avrebbero potuto farlo simulando un qualsiasi orizzonte desiderato, se mai possiamo discutere della bontà della simulazione ma confrontarlo con un inesistente orizzonte astronomico non ha senso.

Non volevo fare il confronto con l`orizzonte astronomico: intendevo solo dire che se la caduta in metri dei rilievi in lontananza dovesse essere inferiore a quella attesa, non vado ad immaginare che queste montagne (alcune alte anche km) siano state riscostruite in qualche deserto americano in scala 1:1! Per questo dicevo che non ha senso confrontare le altezze dei rilievi lunari con gli stessi presenti eventualmente sulla Terra e curvati di conseguenza, ma solo controllare che l`altezza cali opportunamente al variare della distanza.

Non solo, come si vede dalla linea rossa che hai aggiunto alla tua immagine basta che la fotocamera sia leggermente fuori bolla, cosa che è praticamente certa nelle foto reali, per annullare ogni considerazione, dato che non c'è modo per risalire al reale orientamento della camera rispetto alla verticale con la precisione necessaria (se ci fosse non esisterebbero i teodoliti per i rilevamenti di precisione, basterebbe una normale macchina fotografica e un software).

Ma infatti avevo scritto subito che e` importante conoscere con grande precisione l`orientamento della camera; ma per far questo non intendevo usare il profilo d`orizzonte piu` lontano.

Per la precisione se ne puo` parlare -e magari fare anche dei conti- perche` trovando una sagoma abbastanza nitida di un rilievo/oggetto vicino la collimazione potrebbe essere abbastanza accurata. Rimane sempre l`incognita dell`altezza del fotografo, pero` non credo sia cosi` importante come l`orientamento, anche qui bisognerebbe fae qualche conticino.

C'è anche da aggiungere che esisterebbe pure l'ipotesi inversa di quella che scarti tu: cioè che abbiano ricostruito sulla luna decine di km di paesaggio terrestre, ovviamente non materialmente ma modificando ad arte i dati delle sonde.

Questo mi sembra certamente piu` fattibilie.

Per quanto riguarda la foto A14-9486 che intendi usare nell'analisi mi aspettavo di meglio, è controluce e di qualità molto più scarsa rispetto a quelle di A11 che avevi linkato all'inizio del thread. Nutro anche forti dubbi che il rilievo che si vede sia a 3200 m, si vede una roccia sopra l'angolo in alto a destra del LEM che, se queste fossero le distanze, dovrebbe avere dimensioni colossali, giusto per fare un esempio.

Hai ragione sulla qualita`, ma avevo intenzione di iniziare da questa perche` conoscevo gia la posizione della camera. Ci sono altre immagini con rilievi piu` lontani, e per questo piu` adatte (Apollo 15).

L'unica cosa degna di approfondimento che noto nell'immagine è l'ombra del LEM, incoerente con le altre, per giustificarla si dovrebbe ipotizzare una forte inclinazione del terreno alla sua destra. Questa verifica mi sembra fattibile, se si dispone di una buona ricostruzione tridimensionale del sito, mentre sicuramente quella della "caduta dell'orizzonte" non lo può essere.

Si`, infatti era tra le cose che volevo approfondire nella discussione precedente.

doktorenko ha scritto: Scusa, ma non dovrebbe esserci 47°/2 tra parentesi? Il mio conto e sbagliato clamorosamente perche` il risultato e` in radianti e non in gradi, quello giusto dovrebbe essere quindi:

Code:

atan(1/4600)/pi*180= 0.0124 gradi = 45"

Sì, pensavo che 47° fosse già la distanza angolare fra centro e margine, invece se la pellicola è da 53 mm è la distanza tra margine e margine e va divisa per 2, il risultato qui sopra è giusto. Però non è giusto questo:

Anch`io uso la risoluzione orizzontale e la lunghezza focale in px:

Code:

lato diapositiva: 53 mm = 4000 px; focale: 61.1 mm = 4611 px

La risoluzione è angolare e quindi non dipende dalla focale (la focale serve solo a trovare l'ampiezza angolare dell'immagine, una volta stabilita questa ingrandendo/rimpicciolendo l'immagine la risoluzione angolare non varia, varia la risoluzione lineare, misurata in mm per esempio). I pixel sono quelli della foto, io ho preso 4000 come cifra tonda, ma non capisco perchè li rapporti alla focale.

Ma infatti avevo scritto subito che e` importante conoscere con grande precisione l`orientamento della camera; ma per far questo non intendevo usare il profilo d`orizzonte piu` lontano.

Per la precisione se ne puo` parlare -e magari fare anche dei conti- perche` trovando una sagoma abbastanza nitida di un rilievo/oggetto vicino la collimazione potrebbe essere abbastanza accurata. Rimane sempre l`incognita dell`altezza del fotografo, pero` non credo sia cosi` importante come l`orientamento, anche qui bisognerebbe fae qualche conticino.

Sposteresti soltanto il problema della messa a bolla dalla macchina fotografica ai rilievi/oggetti che vuoi usare per la collimazione. Chi ti dice qual è il loro orientamento con precisione inferiore al decimo di grado? Nemmeno se fossi sul posto con la livella in mano potresti accertartene, anzi, avresti enormi problemi anche col già menzionato teodolite. Tanto per capirci, alle nostre latitudini 0.1° è la deviazione della verticale gravitazionale rispetto alla verticale geometrica, cioè il filo a piombo, o la bolla, hanno una deviazione intrinseca di 0.1° rispetto alla direzione del centro della terra, per quanto possano essere precisi. Eppure questo non è essenziale in quasi nessuna applicazione pratica e non se ne accorge nessuno. Quello che vorresti fare tu è come verificare questa deviazione della forza di gravità usando le fotografie scattate in una scampagnata, mi sembra ben oltre i limiti del possibile.

Prendo spunto dal metodo della parallasse di OLEG OLEYNIK ; riporto i passaggi per come li ho capiti:

teoria:

1) date due fotografie I_1 e I_2, che variano solo per la rotazione della camera R_1 e R_2
2) I_1 puo` essere trasformata in I_2 e viceversa (naturalmente nei punti inquadrati da entrambe) mediante una deformazione omografica (8 gradi di liberta`)
3) aggiungendo anche la traslazione della camera, la 1) vale solo solo per i punti giacenti sullo stesso piano

metodo Oleynik:

a) date due pose I_1 e I_2, due rotazioni della camera R_1 e R_2 (incognite), e due posizioni P_1 e P_2 (incognite)
b) i punti che compongono lo sfondo (+3km) possono essere considerati appartenenti allo stesso piano

procedura:

1) dalle immagini tolgo tutto cio` che non e` sfondo, ottenendo S_1 e S_2
2) calcolo la matrice H di trasformazione omografica di S_1 in S_2
3) applico la deformazione H all`immagine I_2, ottenendo l`immagine I_h
4) I_h e` l`immagine corrispondente ad una posa fotografica ripresa da una camera ruotata secondo R_1 e traslata di T=P_2-P_1 rispetto a I_1
5) I_1 e I_h sono quindi due scene inquadrate dallo stesso angolo e traslate di T; posso percio` calcolare la distanza degli oggetti in comune nelle due scene mediante la parallasse

Sfruttando questo metodo pensavo di:

Dopo allego i calcoli e le prove con i modelli 3d.

Avevo già incontrato il metodo di Oleynik in un'altra discussione, sia l'idea che i risultati sono molto interessanti. Aspettavo di vedere i tuoi risultati per rispondere, ma credo che per come hai impostato le cose non potranno arrivare.

doktorenko ha scritto: Prendo spunto dal metodo della parallasse di OLEG OLEYNIK ; riporto i passaggi per come li ho capiti:

teoria:

1) date due fotografie I_1 e I_2, che variano solo per la rotazione della camera R_1 e R_2
2) I_1 puo` essere trasformata in I_2 e viceversa (naturalmente nei punti inquadrati da entrambe) mediante una deformazione omografica (8 gradi di liberta`)
3) aggiungendo anche la traslazione della camera, la 1) vale solo solo per i punti giacenti sullo stesso piano

Iniziamo a chiarire la teoria. Quello che conta nelle due fotografie è che siano scattate dalla stessa posizione, angolazione e focale possono essere diverse. A questo punto basta stabilire una corrispondenza fra quattro punti delle due immagini, a tre a tre non allineati, per poter ricavare la proiettività, o omografia, fra le due immagini (matematicamente si trova di una funzione fra due piani proiettivi). Cioè ricavata la matrice H possiamo ricostruire la seconda immagine semplicemente applicando H a tutti i punti della prima. Particolare non insignificante: per riuscire a trovare H bisogna conoscere un poco di teoria degli spazi proiettivi, partendo dall'impostazione per ricavare un'omografia riportata su wikipedia H si ricava in modo assai diverso da come si farebbe per un normale sistema. Questo perchè non è una funzione tra punti dello spazio tridimensionale, ma fra piani proiettivi, magari in un altro commento spiegherò un po' più in dettaglio.

Aggiungendo una traslazione della camera non esiste più nessuna omografia, però i punti all'infinito non risentono della traslazione ed è su questo fatto che si basa il metodo di Oleynik. Quello che fa è ricavare la proiettività H scegliendo i quattro punti fra quelli "all'infinito", per i suoi scopi basta che siano ad almeno un paio di km di distanza, quindi applicandola alla prima immagine ottiene una nuova immagine il cui sfondo coincide con quello della seconda. Tutti i punti che non sono all'infinito (nel senso già chiarito) non verranno a coincidere per via dello spostamento della fotocamera, ci sarà quindi una parallasse. Misurando questa, e conoscendo già la differenza nella posizione fra i due scatti, più la distanza di qualche oggetto vicino (per esempio del margine inferiore dell'immagine, che può essere ricavata dalla focale e dall'altezza del cavalletto), può ricavare tutte le altre distanze degli oggetti che non si trovano sullo sfondo.


Veniamo ora ai tuoi propositi.

Sfruttando questo metodo pensavo di:

Code:

1) ricostruire lo sfondo S_2 (+3km) mediante modellazione 3d dei dati altimetrici, con posizione e rotazione approssimativa R_2 e P_2 2) estrarre lo sfondo S_1 dalla foto Apollo 3) calcolare la matrice H S_1=S_2 4) decomporre la matrice H per ottenere R e T 5) sapendo che R = R_2-R_1 e T = P_2-P_1, risalire a R_1 e P_1

Al punto 1) si presenta già il problema fondamentale di cui parlavo nei commenti sopra, e cioè l'aggettivo "approssimativa". Se vuoi misurare una grandezza di circa 0,1° va da sè che la precisione iniziale deve essere molto maggiore, diciamo almeno un ordine di grandezza, cioè 1/100 di grado. Questo perchè l'errore dei dati iniziali si amplifica durante i calcoli (propagazione dell'errore). Quindi se non hai una ricostruzione 3D esatta al cm, con uguale precisione nella posizione della fotocamera -compresa la sua altezza dal suolo, determinante- e soprattutto una precisione di almeno 0,01° nella sua rotazione, tutto quello che segue è inutile perchè il risultato finale sarà affetto da un'imprecisione non inferiore al valore che vuoi misurare.

Facciamo però finta che al punto precedente hai una precisione assoluta, tanto nella ricostruzione 3D quanto nei dati relativi alla fotocamera. A questo punto ti converrebbe nella tua ricostruzione orientare la camera perfettamente in verticale, in questo modo puoi scegliere i 4 punti sullo sfondo dell'immagine Apollo, trovare i corrispondenti nella tua ricostruzione, calcolare la matrice H e applicarla alla foto Apollo, ottenendo così una immagine perfettamente a bolla.

Fatto ciò non dovresti far altro che verificare la distanza fra la linea orizzontale a metà immagine (orizzonte astronomico) e lo sfondo. I punti del tuo elenco 4) e 5) non hanno senso perchè la matrice non contiene nessuna informazione sullo spostamento della fotocamera, essendo stata ottenuta ipotizzando che non ci sia nessuno spostamento. Per trovare lo spostamento dovresti se mai usare il metodo Oleynik all'inverso, ma come abbiamo visto non ce n'è nessun bisogno perchè abbiamo già l'immagine che ci interessava.

Resta da capire quale sarebbe la precisione dell'immagine finale, ricavata per ipotesi -assai irrealistica- da una ricostruzione infinitamente precisa. Innanzitutto c'è l'errore nella posizione della macchina fotografica, che non possiamo conoscere esattamente. Un errore di un metro comporterebbe già un errore iniziale del 20% circa della grandezza che vuoi ricavare alla fine. Poi c'è l'errore nell'identificare i 4 punti, che potrebbe anche dipendere semplicemente da un piccolo errore nella scansione digitale della foto, potrebbe anche essere inferiore al pixel, quindi non misurabile. Tutti questi errori comportano che la matrice H sia in realtà H+e_H, dove e_H è il suo errore, e una stima prudente dice che questo errore sia almeno 4-5 volte l'errore iniziale nei dati.

Questi sono i motivi per cui ritengo impossibile fare la tua verifica. Ci sarebbe una ulteriore obiezione: se il lavoro di Oleynik è corretto lo sfondo non si trova affatto a 3 km ma a poche centinaia di metri. Dato che questa è la premessa del tuo ragionamento, se fosse falsa risulterebbe automaticamente inutile tutto ciò che segue, da premesse false può seguire tutto e il contrario di tutto: l'implicazione (formale) A=>B è sempre vera se A è falsa.

Intanto ti rispondo brevemente su questi punti; in seguito approfondiremo quando, se Dio vuole, avro` preparato i modelli 3d per le prove: cerca di avere pazienza :popcorn:

FranZeta ha scritto: Ci sarebbe una ulteriore obiezione: se il lavoro di Oleynik è corretto lo sfondo non si trova affatto a 3 km ma a poche centinaia di metri. Dato che questa è la premessa del tuo ragionamento, se fosse falsa risulterebbe automaticamente inutile tutto ciò che segue, da premesse false può seguire tutto e il contrario di tutto: l'implicazione (formale) A=>B è sempre vera se A è falsa.

Quest`obiezione l`avevo sollevata anch`io, nella discussione precedente, in merito al lavoro di Oleynik: cioe` se lo sfondo non e` virtualmente all`infinito -ovvero i punti presi come riferimento non giacciono sullo stesso piano- non e` possibile usarli per ottenere la matrice H che trasforma una posa nell`altra, e quindi poter calcolare la parallasse; ma e` pur vero che se lo sfondo non e` veramente "sfondo", ma abbastanza vicino, la parallasse sara` evidente sullo (pseudo)sfondo stesso: quindi di riffa o di raffa il sistema dovrebbe funzionare.

Nel mio caso, invece, confronterei le altezze angolari di due rilievi: uno supposto sullo sfondo e uno piu` vicino; il mio sistema pero` dovrebbe essere piu` sensibile all`accuratezza del posizionamento delle camera.

Facciamo però finta che al punto precedente hai una precisione assoluta, tanto nella ricostruzione 3D quanto nei dati relativi alla fotocamera. A questo punto ti converrebbe nella tua ricostruzione orientare la camera perfettamente in verticale, in questo modo puoi scegliere i 4 punti sullo sfondo dell'immagine Apollo, trovare i corrispondenti nella tua ricostruzione, calcolare la matrice H e applicarla alla foto Apollo, ottenendo così una immagine perfettamente a bolla.

Questo e` proprio quello che intendevo fare: la mia inquadratura prevede proprio la camera a piombo; cosi` avevo scritto nel messaggio originale, poi nella modifica successiva ho riscritto "camera ruotata approssimativamente".

Adesso passo a illustrare la procedura di estrazione delle linee dei rilievi nella ricostruzione tridimensionale; prendiamo un caso semplificato:

1) la camera e` in bolla (comunque questo vale sempre, visto che nell`originale si discosta di pochi gradi da questa condizione, e la porzione di inquadratura che viene tagliata e` quella, poco interessante, ai piedi del fotografo)
2) la camera e` orientata convenzionalmente in direzione Sud (verso positivo dell` asse V dei dati altimetrici, questo per trattare il caso piu` semplice)
3) apertura del campo visivo inferiore ai 45 gradi

Procedura:

a) per prima cosa applico la curvatura ai nostri dati altimetrici:

Se la calotta sferica e` poco estesa, possiamo prendere:

Nella posizione della camera la caduta e` zero: e` cioe` la sommita` della nostra calotta sferica
(successivamente possiamo discutere anche sull`eventuale interpolazione del dato altimetrico)

z(u,v) e` quindi una matrice delle stesse dimensioni di h(u,v), con i dati abbassati in proporzione alla distanza dalla camera.

b) rimappatura dei dati, secondo angolo e distanza da una camera oscura di queste caratteristiche:

(metto una dimensione della diapositiva/scansione intera per semplificare):

Immaginiamo ora che z(u,v) sia una griglia di punti su di un piano cartesiano, e una riga di pixel siano punti allineati di coordinate px_i(-2000 ... 2000,-F), con i l`indice del pixel da -2000 a 2000.

Da ogni px_i faccio partire una retta r_i passante per O(0,0), e calcolo i punti di intersezione tra queste rette con le rette sulle quali giacciono i punti z(u,v) allineati per righe v.

Ho ottenuto quindi, mediante una scansione di raggi partenti da una riga di pixel e passanti per O, una nuova griglia di altezze z(u,v) -> h_a(i,v), con i lo scostamento angolare a = atan(i/F) e v la distanza dalla camera.

Se avete notato, la trasformazione non cambia v: questo perche` possiamo considerare i punti di una stessa retta parallela al piano di proiezione tutti alla stessa distanza; ossia lo scostamento angolare dal centro avvicina i punti in rapporto al cos(a).

c) proiezione

Indichiamo ora con x e y i pixel dell`immagine da ottenere mediante proiezione attraverso il foro stenopeico O sul piano a distanza focale |F|
Trattiamo una colonna c di dati h_c = h_a(c,1...profondita` di campo) alla volta:

Ho quindi due triangoli rettangoli simili con i cateti corrispondenti:

Ogni colonna y_c alla fine conterra` i dati delle altezze dei rilievi di maggior altezza relativa proiettate sul sensore, ordinate secondo la distanza d dall`operatore: i massimi locali di ogni colonna formeranno le linee dei rilievi. (non so se ho considerato il ribaltamento dell`immagine proiettata, ma il concetto non cambia)