- Messaggi: 109
- Ringraziamenti ricevuti 52
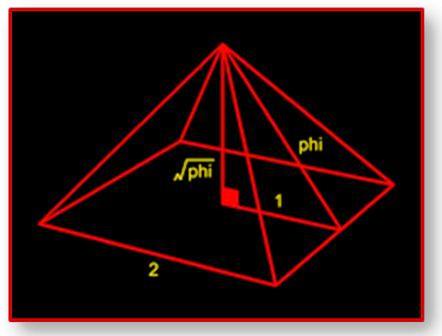
Il soffitto di Micerino
- il primo è del tardo 1700, in Inghilterra:
- il secondo è di fine 1800, in Italia:
Ho scelto due foto con il riflesso sull'acqua, perché forse qualcuno capirà a colpo d'occhio dove voglio arrivare.
Il primo ponte è sorretto da una struttura a semicerchio, mentre il secondo dispone di un sostegno a parabola.
Durante la prima metà dell'800, nel periodo tra i due ponti, si sono evoluti nuovi modelli matematici, che hanno accertato quello che già sospettava Galileo due secoli prima: in una struttura orizzontale, appoggiata sulle due estremità, lo sforzo si distribuisce seguendo un andamento parabolico.
Pertanto, tra le numerose proprietà della parabola, c'è anche questa: è la migliore struttura possibile per sostenere un carico.
Prima di andare avanti, voglio ricordare che il primo a tentare uno studio sulle coniche (tra cui la parabola) fu Apollonio di Perga, nel III secolo a.C.
Ora diamo un occhiata a questa stanza:
E' quella che chiamano "camera sepolcrale" di Micerino, Faraone d'Egitto del 2600 a.C.
Si trova sotto una quindicina di metri di roccia compatta, nel sottosuolo della relativa piramide, ed è protetta da 18 blocchi di granito che formano il soffitto; ognuno di essi è stato tagliato con quella curvatura che vedete.
Vi chiedo di concentrarvi su quella curva, che di sicuro non è un arco di circonferenza.
Secondo voi, è una parabola?...
Siamo 2300 anni prima di Apollonio, 4300 prima di Galileo e 4500 prima del Ponte di S. Michele.
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Si prega Accesso a partecipare alla conversazione.
- horselover
-

- Offline
- Utente
-

- Messaggi: 254
- Ringraziamenti ricevuti 14
Si prega Accesso a partecipare alla conversazione.
Come può l'acqua memoria serbare se dalle nuvole cade? (poeta del dugento)
Ci sposiamo sessiamo insieme sessista bene perché no (progetto anti gender 2016)
Si prega Accesso a partecipare alla conversazione.
horselover ha scritto: è chiaro che gli antichi avevano conoscenze superiori alle attuali.
Ovviamente... altrimenti non esisterebbe questa sezione dedicata agli OOPART.
Tuttavia, appena ci ho messo piede ho trovato un topic che li mescola tutti insieme, probabilmente con l'intenzione (del tutto legittima) di creare un elenco.
Avendo fatto il moderatore per 6 anni, in tutt'altro forum, trovo più produttivo discutere un OOPART in ogni topic; ognuno con il suo titolo, a beneficio di chi ci legge.
Questo è il primo che propongo. Secondo l'interesse che raccoglierà, vedremo se andare avanti.
Ripropongo la mia domanda con un'estensione.
Oltre a quelli che valuteranno "a occhio", come ho fatto io, c'è nessuno che dispone di un qualche software per verificare se è una parabola?
Chessò... un ingegnere edile, un matematico, un progettista CAD...
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Si prega Accesso a partecipare alla conversazione.
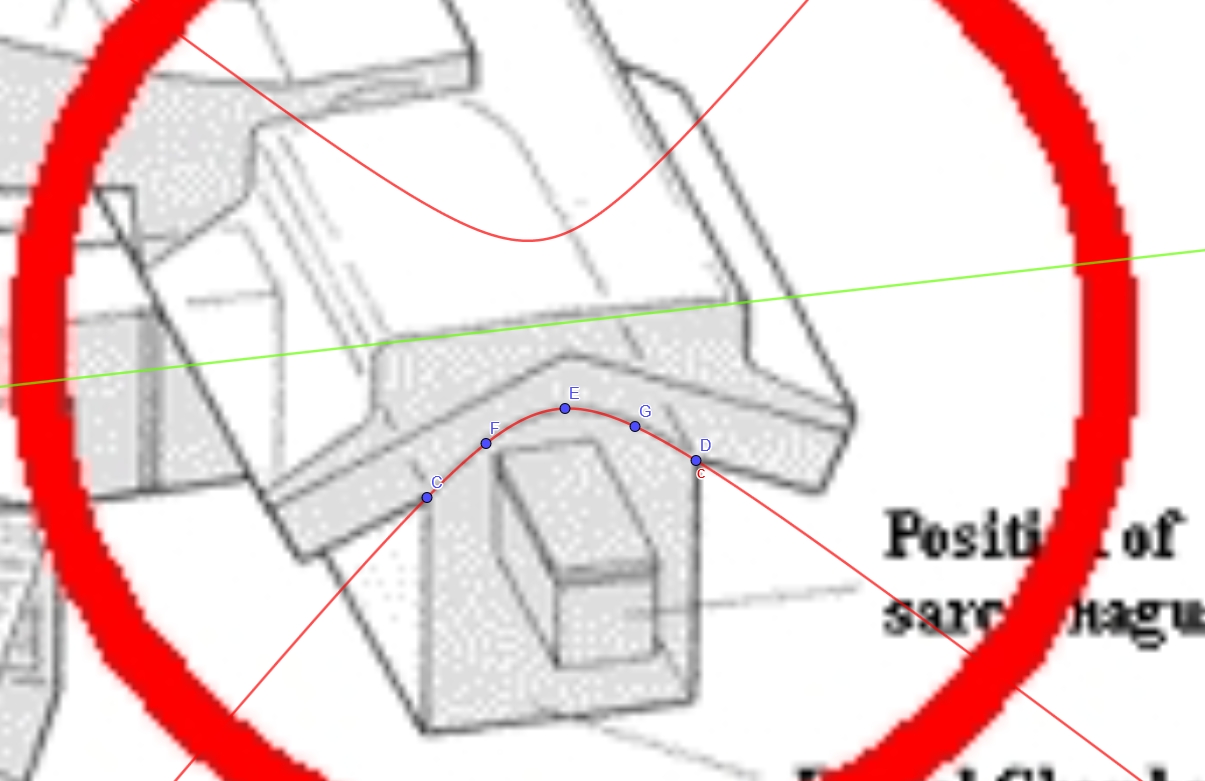
Si può fare una verifica in modo molto semplice usando il programma Geogebra che è gratuito e disponibile anche in versione online, senza bisogno di scaricarlo. Si incolla l'immagine direttamente sul piano cartesiano, poi si utilizza lo strumento "conica per cinque punti" e questo è il (mio) risultato:
Come vedete la curva rossa, conica passante per C-D-E-F-G, segue bene il profilo dell'arco, solo che si tratta di un'iperbole, quindi l'arco non è parabolico. Per confronto ho tracciato in arancione la parabola che ha stesso fuoco e vertice, rispettivamente H ed E. Ovviamente il procedimento ha la precisione che si può ottenere marcando i cinque punti sulla foto, però bisogna considerare che se c'è un'iperbole che approssima bene una curva non può esserci una parabola che la approssima altrettanto bene. Più precisamente: se per cinque punti passa un'iperbole non c'è nessuna parabola che passa per gli stessi cinque punti. Inoltre che l'immagine non sia esattamente frontale non fa differenza, dato che una rotazione della fotocamera non modifica il tipo affine della conica* (ellisse, iperbole o parabola).
Resta il fatto che ufficialmente le sezioni coniche sono curve note a partire da solo un paio di secoli prima di Apollonio, quindi ciò fa effettivamente di quel soffitto un OOPART.
*Qui serve una precisazione: in effetti una proiezione può modificare il tipo affine della conica, anzi, può trasformare indifferentemente una conica in un'altra e ogni conica in una circonferenza. Ma parlando di proiezioni fotografiche non si raggiungono mai i casi limite che comportano la trasformazione, e comunque non è certo la situazione della nostra immagine.
FranZη
Si prega Accesso a partecipare alla conversazione.
Non conoscevo Geogebra, ma ero quasi certo che esistesse qualcosa di simile.
Adesso, la tua risposta produce un'altra domanda.
L'iperbole, come la parabola, non è una curva che si intuisce così, a fantasia, come la circonferenza.
Ci servirebbe pertanto un ingegnere o un architetto, qualcuno specializzato in Scienza delle costruzioni, per sapere qualcosa sulle caratteristiche dell'iperbole.
È possibile che su una struttura in pietra sia più efficace della parabola?
Anche se non lo fosse, è possibile che sia comunque più efficace della banale circonferenza?
Speriamo ci sia qualcuno in grado di rispondere...
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Si prega Accesso a partecipare alla conversazione.
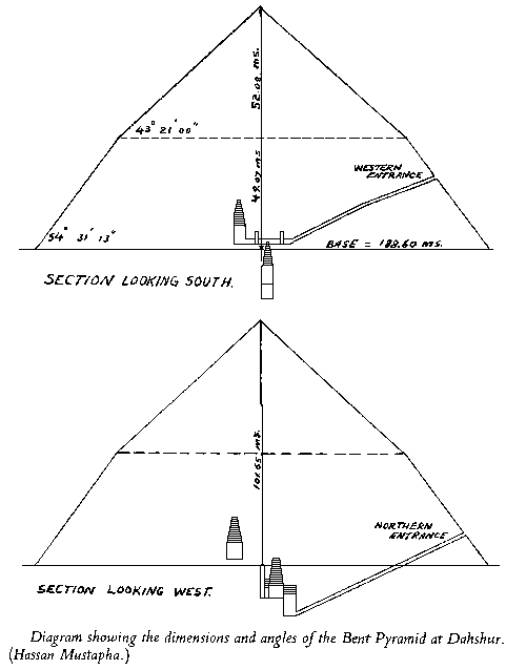
che regge comunque senza problemi la struttura sovrastante. Non solo: ad occhio sembrerebbe una struttura scavata nella roccia al di sotto della piramide, questo escluderebbe ogni utilità del profilo della volta, dato che prima di mettere in posa i blocchi del soffitto avrebbero dovuto scavare un vano più ampio in grado di reggere da solo il peso della piramide. Infine avevano già delle soluzioni molto valide, tipo questa:
che si trova nelle camere della Piramide Romboidale di Dahshur, soluzione molto simile a quella della grande galleria nella Piramide di Cheope. Tornando alle coniche, scoprirle non è una cosa che richieda molta genialità, basta una torcia elettrica e le trovate tutte proiettate su un muro. Si potrebbe obiettare che 25 secoli prima di Cristo non esistevano torce elettriche (forse...), ma un qualche tipo di lampada che emettesse un fascio di luce conico l'avranno sicuramente avuto. Certo che dal dire "toh, che strana curva" guardando un ombra sul muro ad indagarne le proprietà matematiche, come fece Apollonio, di strada ce ne passa parecchia.
In particolare solo uno studio matematico dell'iperbole porta alla scoperta del secondo ramo, visto che l'ombra della torcia proietta solo un ramo della curva; ecco allora che un soffitto con profilo iperbolico potrebbe suggerire, a chi ha sufficienti conoscenze teoriche, che al di sopra della camera si trovi qualcos'altro, in corrispondenza di quello che sarebbe il secondo ramo dell'iperbole. La butto lì senza nessuna pretesa che possa essere una spiegazione efficace , solo a mo' di esempio.
**********************
Già che è stata nominata, anche la Piramide Romboidale secondo me potrebbe meritare una sezione sua in queste discussioni. E' la famosa piramide a doppia inclinazione, attribuita al faraone Snefru (che oltre a questa avrebbe fatto costruire altre due enormi piramidi, di 92 e 105 metri d'altezza!):
La piramide è alta quasi esattamente quanto la Piramide Rossa, di 105 metri, che le sta di fronte; la parte superiore della piramide è inoltre una copia in scala 1:2 di quest'ultima. Qualcuno ha ipotizzato che si trattasse di un impianto di produzione di energia, funzionante secondo modalità sconosciute, certamente il fatto che le due piramidi siano in scala suggerisce fenomeni di risonanza. La spiegazione ufficiale invece è una autentica barzelletta: arrivati a metà costruzione i progettisti si sarebbero accorti che sarebbe venuta fuori troppo alta e sarebbe crollato tutto, avrebbero allora deciso di ridurre l'angolo e farla più bassa. Una volta verificato che il tutto stava in piedi, siccome al faraone non gli garbava la piramide storta, ne avrebbe fatta costruire un'altra lì vicino, alta sempre più di 100 metri, usando l'inclinazione della parte sommitale della Piramide Romboidale, che si era dimostrata stabile. Anche il più ignorante dei manovali saprebbe formulare un'ipotesi più seria di questa dell'egittologia ufficiale...
FranZη
Si prega Accesso a partecipare alla conversazione.
Un'idea interessante... ma non sono convinto per altri motivi.FranZeta ha scritto: che il profilo di quel soffitto abbia un significato simbolico piuttosto che ingegneristico
Io ci sono stato, lì dentro, e ti posso garantire che non è affatto agevole.
Prima devi passare 30 metri di cunicolo in discesa, con una pendenza che la macchina farebbe in prima.
Per passarci ti devi abbassare, perché in sezione fa circa un metro e mezzo.
Poi hai una ventina di metri "tranquilli", in pianura e con buona ampiezza, ma quando arrivi all'anticamera c'è un altro cunicolo discendente: saranno 10-12 metri, però è decisamente più ripido del primo.
Ogni blocco del soffitto pesa circa 800 kg. Stanno a oltre 3 metri di altezza, in una stanza larga poco più di due metri.
Anche senza contare la lavorazione meticolosa, con la curvatura iperbolica e la squadratura perfetta, il solo trasportarli fin lì era quasi impossibile.
Trovo strano che tutto 'sto sudore sia servito a rispettare un simbolismo.
Cioè... vuoi un'ipebole "simbolica"?... Va bene, vorrà dire che scolpiremo il soffitto con quella forma, direttamente sulla roccia calcarea.
Tanto è simbolico... chissenefrega di portare laggiù 18 blocchi da 800 kg?
Inoltre, non s'è mai vista una conica in tutto l'Egitto dinastico, da Narmer fino a Cleopatra (tranne la banale circonferenza).
Anche nel caso di Micerino, quell'iperbole l'hai scoperta tu con Geogebra; nessuno se n'era mai accorto.
In tutte.nella camera adiacente è usata una soluzione molto più primitiva
Quella che mostri è la "camera delle 5 nicchie", ma è così anche l'anticamera, il vestibolo ed i corridoi.
Solo la camera sepolcrale, o presunta tale, ha quel particolare soffitto.
Lo è, come anche quella di Chefren.ad occhio sembrerebbe una struttura scavata nella roccia al di sotto della piramide
Fra quelle tre, solo quella di Cheope ha delle stanze interne, le altre due le hanno nel sottosuolo.
C'è una decina di metri di roccia calcarea, tra il soffitto iperbolico e la base della piramide.avrebbero dovuto scavare un vano più ampio in grado di reggere da solo il peso della piramide.
Esiste anche un'apertura, visibile dall'anticamera, dove i blocchi sono accessibili dall'alto. Tra il soffitto e la roccia calcarea c'è un vuoto di 10-15 cm; una mano aperta in verticale non ci passa (ho provato).
Questo escluderebbe anche la tua supposizione (comunque interessante) sul secondo ramo dell'iperbole.
L'aggetto è una soluzione validissima, ma puoi usarla nelle piramidi con stanze interne, non sotterranee.Infine avevano già delle soluzioni molto valide
A Dashur, il soffitto aggettato è stato adottato anche nella Piramide Rossa, ma in quel caso è normale: durante la costruzione, piazzi quei lastroni leggermente spostati all'interno, mentre sali verso l'alto.
Altra cosa è scavare un aggetto sotterraneo, a colpi di piccone.
Se ci apri un topic, io ci sono. Ho diverse battute divertenti, sulla spiegazione ufficiale.Già che è stata nominata, anche la Piramide Romboidale secondo me potrebbe meritare una sezione sua in queste discussioni.
Trovo che la tua sia un po' troppo creativa, ma qualsiasi ipotesi è più credibile di Zahi Hawass (per fortuna l'hanno cacciato via).
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Si prega Accesso a partecipare alla conversazione.
Rox2 ha scritto: Trovo strano che tutto 'sto sudore sia servito a rispettare un simbolismo.
Cioè... vuoi un'ipebole "simbolica"?... Va bene, vorrà dire che scolpiremo il soffitto con quella forma, direttamente sulla roccia calcarea.
Tanto è simbolico... chissenefrega di portare laggiù 18 blocchi da 800 kg?
Beh con "simbolico" intendevo qualunque scopo che non sia prettamente pratico, anche perchè appurato che si tratta di un controsoffitto viene a mancare qualsiasi funzionalità strutturale. Poi vai a sapere che cosa gli passava per la testa a chi ha scavato quelle stanze, tra parentesi ho qualche dubbio che abbiano usato solo picconi, i quali in teoria avrebbero dovuto essere di rame o al massimo bronzo, dato che ufficialmente non disponevano di materiali più adatti.
Comunque la faccenda del controsoffitto mi ha incuriosito, così ho ritracciato l'iperbole e stavolta ho incluso anche il secondo ramo:
...poi ho trovato, purtroppo con una risoluzione pessima, uno spaccato dell'interno della tomba, e il risultato (al netto delle approssimazioni di tutto il procedimento) è interessante:
...cioè il soffitto della camera si può situare con precisione nell'asse dell'iperbole. Cosa possa significare tutto ciò non saprei proprio immaginarmelo.
FranZη
Si prega Accesso a partecipare alla conversazione.
Franz, non siamo tu ed io che dobbiamo immaginarcelo.FranZeta ha scritto: Cosa possa significare tutto ciò non saprei proprio immaginarmelo.
E' ora di buttare dentro un po' di sana dietrologia.
Quella stanza è stata scoperta nel 1837. Da allora, orde di studiosi sono andati lì dentro da tutto il mondo: musei, università, istituti di ricerca, case editrici...
Volendo, ci sarebbe da discutere sul fatto che "era vuota, perché depredata dai tombaroli". (Come al solito, con i tombaroli si spiega sempre tutto.)
Il colonnello Vyse ricorse alla dinamite per entrarci dentro, altri passaggi non ce ne sono... Da dove sarebbero passati i tombaroli, non l'ha mai spiegato nessuno. Vabbè...
Io ho un po' di libri sull'argomento, ma non ho nessuna laurea in Egittologia. In quella stanza ero un semplice turista, eppure il mio occhio fu attratto dalla curvatura di quel soffitto, così simmetrica ma evidentemente non circolare.
D'accordo, ho preso una cantonata pensando alla parabola; ma senza Geogebra, nemmeno tu avresti individuato la conica a occhio nudo.
Ciò che appare inquietante è il risultato: dopo 181 anni di presunti fuoriclasse, archeologi di fama mondiale, provenienti dalle massime istituzioni del settore...
(tieniti forte)
...quell'iperbole la scopri tu in una chiacchierata su un forum, usando un software on-line accessibile a chiunque, in seguito alla segnalazione di un turista che ti ha mostrato una foto.
Che fine hanno fatto tutti gli esperti plurilaureati?
Ci sono due alternative, per spiegarlo:
1) L'archeologo professionista non è tenuto ad avere competenze matematiche; anche se lì dentro ci campa, non è detto che si accorga di un'evidenza colossale, notata in pochi secondi da un banale turista.
Ma allora... mandiamolo a zappare l'orto, non a cercare reperti.
2) Quell'archeologo ha visto benissimo quello che ho visto io, quindi l'ha anche studiato e si è accorto dell'iperbole molto prima di noi due. Ma siccome va contro le teorie consolidate, ha capito che divulgando la notizia si giocava la carriera.
Quindi ha taciuto... per non andare a zappare l'orto.
Se qualcuno ha un'altra spiegazione, sono tutto orecchi.
Ah... No... Aspettate... Ce l'ho io!
3) Gli operai hanno lavorato quei blocchi per dargli una curvatura qualsiasi, perché il solito triangolo isoscele non piaceva al faraone.
Per uno scherzo del destino gli è venuta fuori un'iperbole perfetta, il cui asse concide, del tutto casualmente, con il soffitto superiore.
Pertanto, gli archeologi professionisti la ignorano, perché le coincidenze casuali non hanno rilevanza scientifica.
Sono sicuro che Piero Angela sceglierebbe la n° 3.
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Si prega Accesso a partecipare alla conversazione.
Rox2 ha scritto: 1) L'archeologo professionista non è tenuto ad avere competenze matematiche; anche se lì dentro ci campa, non è detto che si accorga di un'evidenza colossale, notata in pochi secondi da un banale turista.
Ma allora... mandiamolo a zappare l'orto, non a cercare reperti.
2) Quell'archeologo ha visto benissimo quello che ho visto io, quindi l'ha anche studiato e si è accorto dell'iperbole molto prima di noi due. Ma siccome va contro le teorie consolidate, ha capito che divulgando la notizia si giocava la carriera.
Quindi ha taciuto... per non andare a zappare l'orto.
Direi che le alternative non si escludono a vicenda. Certamente molti egittologi hanno una formazione prettamente ed esclusivamente umanistica, per cui si fanno un mazzo tanto sui cartigli e iscrizioni varie (alcune delle quali si sono dimostrate essere falsi ottocenteschi, tipo l'iscrizione che attribuisce la paternità della Grande Piramide a Cheope), ma proprio non ci arrivano a fare considerazioni a livello tecnico-scientifico. Però in questi due-tre secoli di egittologia qualcuno con competenze sufficientemente eterogenee per fare i giusti collegamenti c'è sicuramente stato, in buona parte magari si tratta degli autori dei libri "alternativi" che sono certo anche tu avrai letto, ma ci sarà anche qualche egittologo "serio" che tace per i motivi che già hai detto, e forse anche per altre ragioni più sottili ma non meno compromettenti.
Per esempio l'autore dello spaccato che ho riportato sopra, di cui ignoro l'identità, anche se si fosse limitato a riportare planimetrie e quote, qualche dubbio su quello che stava disegnando immagino che l'abbia avuto. Non c'è nemmeno bisogno di usare Geogebra o simili, basta avere le coordinate dei punti e con qualche conto e un po' di pazienza si può arrivare alle stesse conclusioni utilizzando carta e matita. Ma d'altronde questa del soffitto della "tomba" di Micerino è una quisquilia in confronto alle evidenze che riescono a negare, tipo i particolari rapporti matematici della Grande Piramide. Questa discussione mi ha fatto ricordare qualcosa che mi ero appuntato tempo fa, se ti interessa ne ho appena scritto qui .
FranZη
Si prega Accesso a partecipare alla conversazione.
Io posso pure essere d'accordo, ma sui valori numerici hanno una risposta contro la quale non ci possiamo difendere.FranZeta ha scritto: questa del soffitto della "tomba" di Micerino è una quisquilia in confronto alle evidenze che riescono a negare, tipo i particolari rapporti matematici della Grande Piramide.
Ti dicono così:
- Prendo una qualunque cabina telefonica e mi metto a misurarla; le porte, le vetrate, i lati, il telefono...
Tra i valori che ottengo comincio a fare rapporti, moltiplicazioni, proporzioni, radici, percentuali, ecc.
Puoi essere certo che prima o poi troverò, tra i risultati, qualcosa che potrebbe apparire strano, chessò... la successione di Fibonacci, la radice di 2, le proporzioni dell'arca di Noè secondo la Genesi, la latitudine di Babilonia...
Coincidenze che voi dietrologi interpretereste a modo vostro, caricando di misteri affascinanti una banalissima cabina telefonica!
Potrei fare lo stesso con la tua automobile, la tua lavatrice o lo sgabuzzino di casa tua.
Quella risposta è un muro di cemento, non abbiamo armi per demolirla.
L'iperbole che hai (o abbiamo) scoperto, invece, sarà una quisquilia ma è incontrovertibile.
Sono loro a cadere nel ridicolo se provano a negarla.
Devo ricordarti che quello è granito, non la solita roccia calcarea. Immagina le bestemmie, per ottenere quella curvatura precisissima, su una pietra di tale durezza. E l'hanno ripetuto su 18 monoliti tutti uguali!
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Si prega Accesso a partecipare alla conversazione.
No guarda, questo tipo di risposta la conosco piuttosto bene ma non si applica alle proporzioni delle piramidi. E infatti in genere manco ci provano. Se uno mi dice che dalle pietre di Stonehenge si possono ricavare tutti gli allineamenti celesti che vuoi sarei il primo a dover concordare, dato che il calcolo combinatorio lo conosco abbastanza. Ma nel caso delle piramidi c'è un unico parametro che determina tutte le proporzioni: l'angolo alla base. Se quell'angolo ti comporta non solo dei lati in proporzione aurea, ma pure una relazione fra π e Φ, che sono due delle 3-4 costanti matematiche fondamentali, l'inferenza probabilistica è rovesciata e sei tu (tu Piero Angela) a dovermi dimostrare che è assolutamente casuale.Rox2 ha scritto: Io posso pure essere d'accordo, ma sui valori numerici hanno una risposta contro la quale non ci possiamo difendere.
PS Se misurando una cabina del telefono scopri che, per dire, l'altezza misura π volte la base, cosa ne deduci:
a) E' un rapporto puramente casuale;
b) Chi ha progettato la cabina (presumibilmente un ingegnere) conosce il valore di π e l'ha voluto inglobare nel suo pur modesto progetto?
FranZη
Si prega Accesso a partecipare alla conversazione.
- giuseppedifalco
-

- Offline
- Utente
-

- Messaggi: 4
- Ringraziamenti ricevuti 0
Se qualcuno ha un'altra spiegazione, sono tutto orecchi.
Ah... No... Aspettate... Ce l'ho io!
mi dispiace, io non ne ho di spiegazioni perché sono un profano
condivido con voi una riflessione personale che mi viene in mente ogni volta che vedo un manufatto antico che mi piace
secondo me si dà troppa poca importanza alla naturale ricerca della bellezza di un qualunque artigiano/costruttore/artista
l'uomo può talvolta anche avere emulato, o avere provato a farlo, la natura nella sua bellezza, ordine, musicalità, simmetria
Fibonacci è stato un genio che è riuscito a codificare una cosa che già esisteva nei fiori o nelle conchiglie
ma probabilmente non è stato il primo a riconoscerne la bellezza; magari non così in profondità come ha fatto lui, ma di certo non è stato il primo
magari, questa è la spiegazione che mi son dato talvolta, dietro a una scelta costruttiva, artistica, c'è soltanto il desiderio di creare qualcosa che mi piaccia e che piaccia; senza calcoli, senza ragioni, senza secondi fini, senza messaggi nascosti
mio nonno faceva il fabbro ed era molto bravo poiché aveva cominciato da bambino; da un banale pezzo di ferro, a forza di martellate, parolacce e qualche dito rotto tirava fuori fioriere, serrature, chiavi o ferri di cavallo
perfettamente funzionanti; ma molto belle e piene di "inutili" archi, iperboli, parabole, spirali
Si prega Accesso a partecipare alla conversazione.
Veramente, mi è capitato varie volte di sentirglielo dire... Ho riportato l'esempio con parole mie, ma quella cabina telefonica non è una mia idea.FranZeta ha scritto: ...E infatti in genere manco ci provano.
E' passato del tempo, ma forse l'ho sentito proprio da Zahi Hawass, la prima volta.
Ora, visto che ce la stiamo suonando e cantando, permettimi di interpretare il ruolo del "cattivo"... provo a risponderti come farebbe un Angela, se fosse qui.
Quelle non sono due coincidenze, ma una soltanto. La seconda è conseguenza obbligata....non solo dei lati in proporzione aurea, ma pure una relazione fra π e Φ...
Ovvero... Disegnando un triangolo isoscele, che abbia π/2 come rapporto tra base e altezza, è inevitabile ottenere la sezione aurea sul lato obliquo.
...E viceversa.
Lasciando i panni degli Angela e tornando Rox, trovo strano che abbiano applicato anche solo uno dei due rapporti, qualunque sia quello di partenza.
Entrambi i valori sono stati scoperti millenni dopo, quindi ne basta uno soltano per definirlo come OOPArt. Ma se tu li citi entrambi, come fossero indipendenti, quelli ne approfittano: ti fanno passare per "dietrologo che vuole forzare coincidenze inesistenti".
Torno a fare l'avvocato del diavolo, perché anche questa l'ho già sentita.l'altezza misura π volte la base
Non devi dimenticare che un Angela cerca sempre di dimostrare che siamo noi, quelli in malafede.
La loro risposta potrebbe essere questa:
- D'accordo, qui ti è andata bene... Hai trovato il π/2 quasi subito, con la base e l'altezza del triangolo in sezione.
Ma se ti fosse andata male, avresti provato con la proiezione, con la diagonale, con lo spigolo... Qualora non ci fossi riuscito, avresti valutato l'altezza della camera del Re, prima con il pavimento e poi con il soffito, poi avreti preso le misure della grande galleria, l'angolo al vertice, ecc. ecc., continuando all'infinito pur di ottenere qualche dato particolare, da associare ad un "mistero affascinante", allo scopo di chiamare in causa i giganti, gli alieni, gli atlantidei, i viaggi nel tempo, i rettiliani... le vostre solite cazzate.
In sostanza, più cerchi di insistere, più ti fanno passare per "il solito complottista ciarlatano".
Bisogna agire al contrario.
Prima dobbiamo indebolire la diga, accumulando una serie di fatti davvero inspiegabili come l'iperbole di Micerino.
Ce ne sono parecchi altri contro i quali si difendono male, cercando sempre di isolarli per estrapolarli dal contesto. Quando glieli spari in faccia tutti insieme, è possibile che si riesca ad incrinare quel cemento.
Allora sì, che puoi anche snocciolare i tuoi π ed i tuoi Φ, perché a quel punto non ce la fanno più a spacciarli per coincidenze forzate.
P.S.
Rileggendo il tuo post precedente, ho visto che hai citato i "falsi ottocenteschi"; ho intuito il palese riferimento alle iscrizioni "scoperte" da Howard Vyse sopra la camera del re.
Sai perché quel falso, così evidente, viene ancora oggi citato come prova?
Perché il primo a scoprirlo fu Zecharia Sitchin, esperto di lingue antiche, traduttore dal geroglifico, dallo ieratico, dal sanscrito e addirittura dal sumero, ma notoriamente etichettato come "scrittore di fantascienza".
E' senz'altro il più fulgido esempio di Argomentum ad hominem.
Capisci con che gente abbiamo a che fare? ...E tu pensi di affrontarli buttando là un π/2?
Quando ci provai io, l'egittologo che ci faceva da guida mi prese per il culo tutto il pomeriggio.
Riuscì a farlo smettere dicendogli, davanti a tutti: "Provaci tu, a scavare due metri cubi con attrezzi di rame, da un parallelepipedo di granito; quando hai finito chiamami, che ti offro da bere."
Solo a quel punto cessarono le sue battute, sulle proporzioni matematiche.
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Si prega Accesso a partecipare alla conversazione.
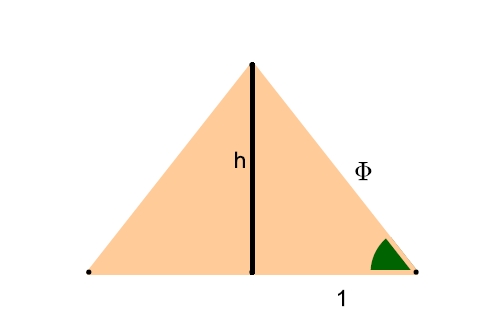
Rox, scusa ma la questione non è come l'hai capita tu. Le proporzioni della Grande Piramide non coinvolgono direttamente π, ma la sezione aurea:Rox2 ha scritto: Quelle non sono due coincidenze, ma una soltanto. La seconda è conseguenza obbligata.
Ovvero... Disegnando un triangolo isoscele, che abbia π/2 come rapporto tra base e altezza, è inevitabile ottenere la sezione aurea sul lato obliquo.
...E viceversa.
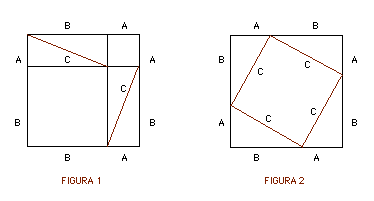
L'altezza risulta essere la radice di Φ, non π, e l'altezza della faccia (l'ipotenusa del triangolo rettangolo) è Φ. Questo è un fatto, nè più e nè meno come il fatto che le piramidi siano allineate ai punti cardinali. Sostenere che sia casuale una è come sostenere che sia casuale l'altra. Poi, oltre a questo dato di fatto, c'è anche l'ulteriore legame alla costante π, che conduce alla relazione fra altezza e perimetro della Grande Piramide. Normalmente è quest'ultimo rapporto che viene segnalato, sia dai ricercatori alternativi che da quelli ortodossi (con fini opposti), ma questo rapporto è secondo me una semplice conseguenza del primo, quello dell'immagine sopra, che non può essere negato senza scadere nel ridicolo, sarebbe come dire che questa figura non rappresenta il Teorema di Pitagora:
Beh, la mia risposta sarebbe questa: se mio nonno aveva il trolley era un tram. Non è che qui mi è andata bene ma poteva andarmi peggio, perchè io in quanto matematico non andrei mai a cercare rapporti strani pensando che abbiano qualche valenza dimostrativa. Ti ho fatto sopra l'esempio di Stonehenge: prendo, che so, 20 pietre, ottengo 190 possibili allineamenti (scegliendo le diverse coppie di pietre), quindi statisticamente posso individuare ogni direzione con la precisione di meno di un grado. Qui si applica l'obiezione di Hawass. Ma alla Grande Piramide direi proprio di no: faccio una sezione della piramide, trovo un triangolo in proporzione aurea, ergo la piramide è stata costruita (e dunque progettata) secondo questa proporzione. C'è poco da controbattere, se non invocando il "caso", qualcuno invece dice "perchè è bello" (un triangolo con quelle proporzioni). Io ricordo la precisione della costruzione: 0,025% di errore rispetto al triangolo ideale.La loro risposta potrebbe essere questa:
D'accordo, qui ti è andata bene... Hai trovato il π/2 quasi subito, con la base e l'altezza del triangolo in sezione.
Ma se ti fosse andata male, avresti provato con la proiezione, con la diagonale, con lo spigolo...
Ti faccio un altro esempio, sempre affine al discorso che stiamo facendo. Non so se hai mai sentito parlare di iarda megalitica, sarebbe un'unità di misura comune a molti siti megalitici, della misura di circa 80 cm. Bene, quando lessi la prima volta di questa unità di misura mi venne subito in mente la Commissione dei Pesi e delle Misure istituita da Napoleone che portò al nostro sistema metrico decimale. Come è noto si partì dalla definizione di metro come decimilionesima parte de semimeridiano terrestre, e da lì vennero definite di conseguenza le altre misure. Immaginiamoci un'analoga commissione in epoca preistorica, messa insieme non da un gruppetto di trogloditi con la clava, ma da una civiltà evoluta, globale e che consce forma e misura del nostro pianeta. Scegliere quel "metro" di ottanta centimetri avrebbe una motivazione piuttosto semplice. Espresse in quell'unità di misura il raggio (equatoriale) e la superficie terrestre risultano essere rispettivamente:
R=8*106 M
S=8*1014 M2
dove con M ho indicato questo particolare "metro" di 80 cm, ossia la iarda megalitica. Con il nostro metro questi due valori sono R=6.378*106 m e S=5.101*1014 m2. Quindi potremmo immaginare che questa antica commissione abbia scelto invece della quarantamilionesima parte della circonferenza terrestre, come quella napoleonica, la cinquantamilionesima parte, che conduce a una misura del raggio e della superficie terrestre espresse dalla stessa cifra - 8 - con diverso esponente (per la verità sarebbe 7.97, ma è un errore simile a quello commesso dalla commissione napoleonica, inoltre non è possibile ottenere un valore intero). Con quest'unità di misura tutti quelli che sono andati a scuola si ricorderebbero le misure della terra per tutta la vita! Mi sembra un'ipotesi suggestiva, ma non ho nessuna difficoltà ad ammettere che potrebbe essere una semplice coincidenza, d'altronde in questo caso sì che ci sarebbero decine di parametri diversi che si potrebbero prendere in considerazione per far quadrare i conti. Ma anche qui, siamo in una situazione completamente diversa da quella delle misure della Grande Piramide.
Per concludere, capisco che questa cosa della curvatura del soffitto ti intrighi, ma il nostro ineffabile Hawass avrebbe una spiegazione delle sue pure per questo: si metterebbe lì nella piana con quattro beduini e un bel pietrone di quelli lì sparsi, poi ci farebbe vedere come con una lampada ad olio si riesce a proiettare un'iperbole sulla pietra, e quelli con lo scalpellino che vanno dietro al profilo fra una martellata sulle dita e una bestemmia in egiziano. Et voilà, lo spettatore sonnecchioso di superquark è più che soddisfatto, e non hanno nemmeno dovuto sbattersi a spiegargli cosa sono π e Φ. Per il resto credo che non abbiamo scoperto nulla, basta un geometra che va lì a prendere le quote del soffitto ed ecco che scopre l'iperbole.
FranZη
Si prega Accesso a partecipare alla conversazione.
giuseppedifalco ha scritto: mio nonno faceva il fabbro ed era molto bravo poiché aveva cominciato da bambino; da un banale pezzo di ferro, a forza di martellate, parolacce e qualche dito rotto tirava fuori fioriere, serrature, chiavi o ferri di cavallo
perfettamente funzionanti; ma molto belle e piene di "inutili" archi, iperboli, parabole, spirali
Capisco quello che intendi, in effetti è vero che certe forme sono ricorrenti in natura, per esempio le coniche vengono fuori da sole in molti contesti diversi. Però un conto è costruire qualcosa che sembra un'iperbole, altro conto è costruire un oggetto effettivamente iperbolico. Anche se sai perfettamente come è fatta un'iperbole o una parabola, se provi a disegnarle a mano libera troverai inevitabilmente delle curve diverse da quelle teoriche, a meno che non conosci il metodo di costruzione geometrica. Ecco, il discorso del soffitto di Micerino è di questo tipo: quella è proprio un'iperbole punto per punto, non una curva che gli assomiglia.
PS Ma sei fuori dalla Tenda Rossa di Nobile?
FranZη
Si prega Accesso a partecipare alla conversazione.
E' esattamente quello che dicevo io, ma evidentemente mi sono spiegato malissimo.FranZeta ha scritto: ...ma questo rapporto è secondo me una semplice conseguenza del primo
Per chi ci stesse leggendo, ricordo che la Piramide di Cheope ha 230 m di lato; in origine era alta 147 m.
Da qui deriva la conversazione di questi ultimi post: dividendo il lato per π/2, si otteniamo 146 metri e mezzo, che al netto di arrotondamenti ed approssimazioni, è il valore dell'altezza.
Ma come mai... da qualsiasi piramide si parta, si finisce sempre a parlare di quella di Cheope?
P.S.
Franz, vedo un tuo quoting dall'utente giuseppedifalco, ma non vedo il suo post.
Non capisco se lo hai copiato da un altro topic...
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Si prega Accesso a partecipare alla conversazione.
Repubblica nel giugno 2009 pubblicava quest'articolo:
www.repubblica.it/2008/06/sezioni/scienz...iramide-perduta.html
sulla quarta piramide attribuita al faraone Djedefra.
L'articolo, oltre palesi assurdità come: "La piramide di Djedefra era imponente e secondo gli ultimi calcoli superava di 7,62 metri la piramide di Cheope" e nello stesso tempo: "Per edificare la piramide ci vollero otto anni di lavoro e oltre 15mila persone"), riporta le stime delle misure:
"La piramide di Djedefra era imponente e secondo gli ultimi calcoli superava di 7,62 metri la piramide di Cheope, alta 146 metri. Ognuna delle singole facce, alla base, misurava 122 metri e l'angolo di inclinazione era di 64 gradi, nonostante una variazione che impediva all'edificio di cadere."
Che rapporto ci sarebbe?

Una stranezza sono le "piramidi satelliti" che un'articolo in inglese descrive: "There are other queries about the two small satellite pyramids. One has been known for a long time, since the work of Perring and Lepsius. Sited at the southwest corner of the main pyramid, one might think it was a pyramid used for the mortuary cult but there was no sign of any funerary objects within it. The other one, discovered in 2002 by the Franco-Swiss team to the southeast of the main pyramid, included a small underground structure with three chambers although above ground it was only 2m50 high with sides 10m long at the base. Apparently on the walls of the chambers were some splendid blue faience tiles like those in the pyramid of Djoser at Saqqara and in the south tomb of the same site. Also found was an alabaster vase 35cm high, fragments of a large alabaster platter and a measuring implement in basalt."
( www.gigalresearch.com/uk/publications-abu-rawash.php )
"A paranoid is someone who knows a little of what's going on. A psychotic is a guy who's just found out what's going on." William S. Burroughs
Si prega Accesso a partecipare alla conversazione.
Ad un certo punto la Storia diventò Mitologia.
Si prega Accesso a partecipare alla conversazione.
- giuseppedifalco
-

- Offline
- Utente
-

- Messaggi: 4
- Ringraziamenti ricevuti 0
FranZeta ha scritto: [quote=PS Ma sei fuori dalla Tenda Rossa di Nobile?
no, sono al bivacco Pelino, sulla cima del monte Amaro 2.793 mslm, massiccio della Maiella, Abruzzo.
Si prega Accesso a partecipare alla conversazione.
Avevo sentito parlare di antiche unità di misura, ma questa non la conoscevo.
Andiamo avanti per ordine...
Ora l'ho visto!Rox2 ha scritto: Franz, vedo un tuo quoting dall'utente giuseppedifalco, ma non vedo il suo post.
Scusate, mi era sfuggito.
Non è che "mi intriga", è che tu ed io siamo i primi a parlarne pubblicamente, anche considerando i ricercatori "eretici" non allineati.FranZeta ha scritto: capisco che questa cosa della curvatura del soffitto ti intrighi
Ho messo la parola "iperbole" sul traduttore di Google, per cercarla anche al di là della solita lingua inglese. Ho tradotto in tedesco, russo, spagnolo, francese... non ricordo più quante lingue ho provato.
Poi gli ho abbinato la parola "Menkaura" (nome originale di Micerino).
Risultato: non ho trovato nulla!
Pare che nemmeno La Settimana Enigmistica abbia mai citato quell'iperbole.
Il fatto che un banale geometra possa scoprilo con un metro tascabile, aggrava la situazione.
Sono stato il primo a definirmi "un semplice turista"; io non sono nemmeno geometra, ma perito elettronico. E anche tu, pur essendo un matematico, hai usato un software di pubblico dominio, che avrei potuto usare anch'io se lo avessi conosciuto.
Hanno versato fiumi di inchiostro su stupidaggini insignificanti, ma nessuno s'è accorto che quella curva sarebbe stata studiata 2300 anni dopo Micerino.
Non più, ormai... La primavera araba ha fatto qualcosa di buono.FranZeta ha scritto: il nostro ineffabile Hawass avrebbe una spiegazione delle sue pure per questo...
Oltre a Mubarak, hanno cacciato a calci anche Zahi Hawass; credo che ora viva negli U.S.A., dopo che nel suo paese è miracolosamente sfuggito al linciaggio.
Comunque, anche se fosse lì, non potrebbe generare un iperbole orientando la luce di una fiamma.
O meglio... Lui potrebbe anche farlo, ma Micerino non poteva. Avrebbe dovuto avere un riflettore a parabola.
Come hai già intuito da solo in quell'articolo c'è una montagna di caz... di inesattezze, voglio essere diplomatico.zeppelin ha scritto: Repubblica nel giugno 2009 pubblicava quest'articolo:
www.repubblica.it/2008/06/sezioni/scienz...iramide-perduta.html
sulla quarta piramide attribuita al faraone Djedefra.
Come al solito, spacciano per certezze le esternazioni di qualche archeologo, che faceva supposizioni nel tentativo di capirci qualcosa.
Di quel faraone non sappiamo manco come si chiamasse: Didufri, Kheper, Radjedef... Oggi va di moda "Djedefra", ma io lo conobbi come "Didufri" e continuo così.
L'ipotesi più plausibile è che fosse un reggente. Sembra che sia salito al potere come fratello di Cheope, in attesa che Chefren diventasse adulto per succedere al padre.
Questo spiegerebbe il suo breve regno, nonché alcuni documenti in cui appare come un usurpatore.
Comunque, la piramide che gli è stata attribuita sarebbe questa:
...Allora tieniti forte, perché quella che ci mostri è la piramide di Chefren: la più facile da costruire, rispetto alle altre due, per una lunga serie di motivi.macco83 ha scritto: Ovviamente per me son state posate da una qualche macchina e non a occhio
Se per quella c'è voluta una macchina, per le altre ci voleva la fantascienza.
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Si prega Accesso a partecipare alla conversazione.
Divertente la precisione al cm del dato "7.62 metri in più" rispetto alla Grande Piramide, quando poi sbagliano di 4 gradi l'inclinazione, dato che con quei valori dovrebbe essere 68° e rotti. Praticamente una torre più che una piramide...Ma come già detto, sembrano decisamente cazzate, anche alla luce dell'immagine postata.zeppelin ha scritto: "La piramide di Djedefra era imponente e secondo gli ultimi calcoli superava di 7,62 metri la piramide di Cheope, alta 146 metri. Ognuna delle singole facce, alla base, misurava 122 metri e l'angolo di inclinazione era di 64 gradi, nonostante una variazione che impediva all'edificio di cadere."
Che rapporto ci sarebbe?
Rox2 ha scritto: Ho messo la parola "iperbole" sul traduttore di Google, per cercarla anche al di là della solita lingua inglese. Ho tradotto in tedesco, russo, spagnolo, francese... non ricordo più quante lingue ho provato.
Poi gli ho abbinato la parola "Menkaura" (nome originale di Micerino).
Risultato: non ho trovato nulla!
Pare che nemmeno La Settimana Enigmistica abbia mai citato quell'iperbole.
Sì capisco, quello che volevo dire è che se si nega una cosa evidente come quella relativa alle dimensioni della Grande Piramide, figuriamoci sta storia del "piccolo" soffitto di Micerino. In effetti non avevo mai fatto una ricerca, pare che al di fuori di superquark e dei testi ortodossi esista un mondo che pensa:
...quindi per quanto riguarda la sezione aurea sono semplicemente arrivato alle stesse conclusioni di chiunque analizzi i numeri senza preconcetti. Tra parentesi nel sito dove ho trovato l'immagine qui sopra si cita Erodoto:
Lo storico greco Erodoto racconta che, secondo i sacerdoti dei templi egizi, la Grande Piramide fu costruita in modo tale che l'area di ciascuna delle sue quattro facce fosse uguale al quadrato della sua altezza
Beh, questa è precisamente la definizione di sezione aurea. Chiusa la parentesi con Cheope.
Per quanto riguarda la "nostra scoperta" che facciamo, la rendiamo nota al mondo e pubblichiamo?
FranZη
Si prega Accesso a partecipare alla conversazione.
Aspetta... mi rendo conto adesso, che forse mi sono spiegato male.FranZeta ha scritto: Per quanto riguarda la "nostra scoperta" che facciamo, la rendiamo nota al mondo e pubblichiamo?
Non avevo alcuna intenzione di vantarmi (insieme a te), come "FranzEta e Rox2: gli autori di una eccezionale scoperta archeologica".
E' proprio la tua ricerca delle geometrie, sul π e sul Φ, che mi offre la possibilità di spiegarmi meglio.
Un banalissimo imbecille di turista, come me, può passare l'intera giornata a fotografare la piramide di Cheope, a girarci intorno, a salirci sopra ed entrarci dentro, ma senza un'attenta analisi non vedrà mai la sezione aurea a colpo d'occhio.
Non vedrà mai nemmeno il π/2.
Io non ci ho pensato nemmeno per un attimo, mentre ero lì, nonostante sapessi già di quelle corrispondenze matematiche.
Invece, quello stesso cliente di Alpitour, quando entra nella camera di Micerino... è impossibile che non veda quel soffitto particolare.
Ripropongo la foto, per evitare di tornare indietro:
Molti avranno studiato al Liceo Classico, al Linguistico, all'Alberghiero, ma Sant'Iddio... Su migliaia di turisti, ce ne sarà qualcuno che viene dall'ITIS, o da un'altra scuola dove c'è un po' di matematica.
Non pretendo le Trasformate di Laplace, ma cazzo... le curve di secondo ordine le studiano pure a ragioneria.
E' questa la differenza, tra la "mia" conica e la "tua" sezione aurea: quel soffitto si vede a colpo d'occhio.
Magari lo scambi per una parabola, come ho fatto io, ma capisci immediatamente che non è la solita circonferenza.
Cerco di riassumere il concetto in poche parole...
L'archeologo sulla piramide di Cheope, che non si accorge del Φ o del π/2, può anche essere giustificabile.
Quello che non vede il soffitto di Micerino, invece, deve cambiare mestiere (oppure è in malafede).
Ciò che cambia è l'evidenza della loro... "distrazione".
P.S.
Se hai modo di divulgare la scoperta, al di fuori di LuogoComune, decidi tu se farlo o meno.
Qualora decidessi di farlo, non merito nessuna citazione; puoi chiamarmi semplicemente "un turista che mi ha segnalato una foto".
Tanto l'ho presa da Wikipedia, quindi è sotto licenza Creative Commons. Le mie sono in formato cartaceo, di un'epoca in cui c'era ancora il rullino.
Non attribuire a malafede quel che si può ragionevolmente spiegare con la stupidità
(Rasoio di Hanlon)
Si prega Accesso a partecipare alla conversazione.
Sì ovvio non cito la grande piramide perchè non ho foto così ben definite. Tralaltro basta confrontare la struttura interna delle due piramidi (Cheope e Chefren) per capire che avevano due funzioni ben diverse. Cmq anche tagliare in quel modo l'obelisco di Luxor e farlo in un pezzo unico è fantascienza per noi. L'obelisco di Washington in confronto è roba da bebè

Ad un certo punto la Storia diventò Mitologia.
Si prega Accesso a partecipare alla conversazione.