- Messaggi: 169
- Ringraziamenti ricevuti 8
Analisi lunari mediante strumenti informatici
- doktorenko
-
 Autore della discussione
Autore della discussione
- Offline
- Utente
-

Less
Di più
5 Anni 6 Mesi fa - 5 Anni 6 Mesi fa #39722
da doktorenko
Analisi lunari mediante strumenti informatici è stato creato da doktorenko
Questa è una discussione sperimentale: nel senso che i partecipanti sono invitati a ripetere e a riprodurre le esperienze proposte; tutto il codice necessario per generare le immagini verrà pubblicato.
Il principio per la formazione delle immagini è quello della camera ottica, ma capovolto per ragioni di efficienza: invece di intercettare un determinato fascio di raggi luminosi riflessi dal soggetto, si inviano dal sensore verso il soggetto tanti raggi quanti sono i punti sensibili della nostra pellicola virtuale; raggi quindi che hanno origine ognuno in un punto distinto del sensore, che passano tutti per uno stesso punto (il cosiddetto foro stenopeico), e che da questo foro di separano per incontrare -eventualmente- la superficie di un soggetto illuminato.
La prima parte del codice è relativa appunto alla formazione di questi raggi; come linugaggio di programmazione uso, per iniziare, python e il modulo numpy.
Creiamo quindi la nostra camera ottica (la convezione 3d usata è: asse y altezza, z profondità) :
La camera "cam" così costruita:
1) ha un sensore quadrato formato da 128*128 punti ("risoluzione")
2) ha centro (inteso come il punto in comune del fascio di raggi proiettato) nel punto (0,.35,-3)
3) ha una focale fissa di .61 e una dimensione del sensore di .55 per lato
4) non si può orientare (punta direttamente l'asse z)
l'origine di ciascun raggio è memorizzata in "cam.o", la direzione in "cam.r"
fine della prima parte
Il principio per la formazione delle immagini è quello della camera ottica, ma capovolto per ragioni di efficienza: invece di intercettare un determinato fascio di raggi luminosi riflessi dal soggetto, si inviano dal sensore verso il soggetto tanti raggi quanti sono i punti sensibili della nostra pellicola virtuale; raggi quindi che hanno origine ognuno in un punto distinto del sensore, che passano tutti per uno stesso punto (il cosiddetto foro stenopeico), e che da questo foro di separano per incontrare -eventualmente- la superficie di un soggetto illuminato.
La prima parte del codice è relativa appunto alla formazione di questi raggi; come linugaggio di programmazione uso, per iniziare, python e il modulo numpy.
Creiamo quindi la nostra camera ottica (la convezione 3d usata è: asse y altezza, z profondità) :
Code:
import numpy as np
prodottoS=lambda a,b: np.sum(a*b,axis=0)
normalizza=lambda a: a/np.linalg.norm(a,axis=0)
class Camera:
def __init__(self,centro,risoluzione):
self.c=np.array(centro).reshape(3,1)
F=.61
mm=.55
xv,yv=np.meshgrid(np.linspace(-.5,.5,risoluzione),
np.linspace(-.5,.5,risoluzione))
zv=np.zeros((risoluzione,risoluzione))-F
o=np.stack((xv*mm,yv*mm,zv))
self.r=-normalizza(o).reshape(3,-1)
self.o=(o+self.c[:,np.newaxis]).reshape(3,-1)
risoluzione=128
cam=Camera([0,.35,-3],risoluzione)
La camera "cam" così costruita:
1) ha un sensore quadrato formato da 128*128 punti ("risoluzione")
2) ha centro (inteso come il punto in comune del fascio di raggi proiettato) nel punto (0,.35,-3)
3) ha una focale fissa di .61 e una dimensione del sensore di .55 per lato
4) non si può orientare (punta direttamente l'asse z)
l'origine di ciascun raggio è memorizzata in "cam.o", la direzione in "cam.r"
fine della prima parte
Ultima Modifica 5 Anni 6 Mesi fa da doktorenko. Motivo: modifica codice per renderlo piu` aderente alla descrizione
Si prega Accesso a partecipare alla conversazione.
- doktorenko
-
 Autore della discussione
Autore della discussione
- Offline
- Utente
-

Less
Di più
- Messaggi: 169
- Ringraziamenti ricevuti 8
5 Anni 6 Mesi fa - 5 Anni 6 Mesi fa #39761
da doktorenko
Risposta da doktorenko al topic Analisi lunari mediante strumenti informatici
Nella seconda parte, il codice che si occupa di calcolare le intersezioni tra le forme geometriche (per il momento solamente sfere) e i raggi che partono dalla camera:
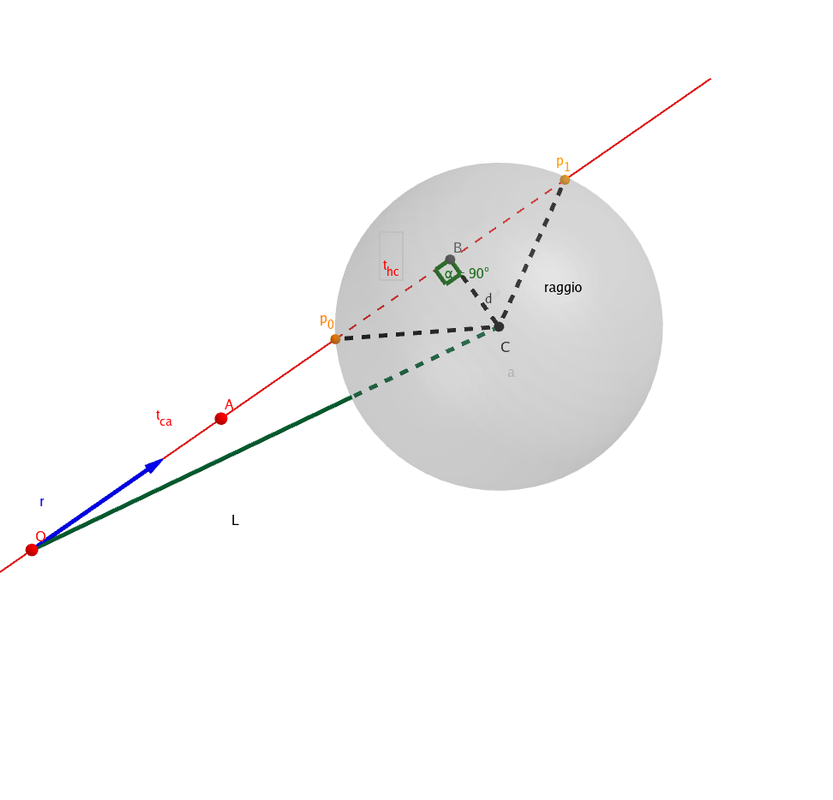
Per Il calcolo dell`intersezione tra raggio e un punto della sfera si procede nella maniera seguente:
1) si traccia L (segmento che unisce il punto di partenza O del raggio al centro C della sfera)
2) si calcola la lunghezza di tca (segmento OB) come prodotto scalare di L per il versore direzione raggio r
3) si ricava la lunghezza di d (cateto BC del triangolo rettangolo OBC)
4) si ricava la lunghezza thc (cateto del triangolo rettangolo CBP, con CP raggio della sfera)
5) si ricavano le due lunghezze t0 e t1 (distanza OP0 e OP1) rispettivamente sottraendo e sommando tca e thc
(il calcolo dei punti tridimensionali P0 e P1 viene eseguito in un secondo momento)
fine seconda parte (qui i dettagli della procedura)
Code:
class Sfera:
C=0
R=[]
n=1
def __init__(self,centro,raggio,colore):
if (self.n==1):
Sfera.C=np.array(centro).reshape(3,1)
self.c=np.array(centro).reshape(3,1)
self.r=raggio
Sfera.C=np.concatenate((Sfera.C,self.c))
Sfera.R.append(raggio)
self.r2=raggio*raggio
self.col=np.array(colore)
self.i=Sfera.n
Sfera.n+=1
def intercetta(self,origine,direzione,d0,ind):
L=self.c-origine
np.seterr(all='ignore')
tca=prodottoS(L,direzione)
d2= prodottoS(L,L)-tca*tca
thc=np.sqrt(self.r2-d2)
t0=tca-thc
t1=tca+thc
t0=np.where(t1<t0,t1,t0)
t0=np.where(t0<0,np.nan,t0)
m=np.where(t0<d0)
d0[m]=t0[m]
ind[m]=self.i
np.seterr(all='warn')
Per Il calcolo dell`intersezione tra raggio e un punto della sfera si procede nella maniera seguente:
1) si traccia L (segmento che unisce il punto di partenza O del raggio al centro C della sfera)
2) si calcola la lunghezza di tca (segmento OB) come prodotto scalare di L per il versore direzione raggio r
3) si ricava la lunghezza di d (cateto BC del triangolo rettangolo OBC)
4) si ricava la lunghezza thc (cateto del triangolo rettangolo CBP, con CP raggio della sfera)
5) si ricavano le due lunghezze t0 e t1 (distanza OP0 e OP1) rispettivamente sottraendo e sommando tca e thc
(il calcolo dei punti tridimensionali P0 e P1 viene eseguito in un secondo momento)
fine seconda parte (qui i dettagli della procedura)
Ultima Modifica 5 Anni 6 Mesi fa da doktorenko.
Si prega Accesso a partecipare alla conversazione.
- doktorenko
-
 Autore della discussione
Autore della discussione
- Offline
- Utente
-

Less
Di più
- Messaggi: 169
- Ringraziamenti ricevuti 8
5 Anni 6 Mesi fa #39774
da doktorenko
Risposta da doktorenko al topic Analisi lunari mediante strumenti informatici
Terza parte.
Aggiungiamo una funzione che restituisce la distanza tra l`origine di ciascun raggio e l`eventuale oggetto incontrato (contestualmente viene restituito anche l`indice dello stesso oggetto). Se il raggio non incontra ostacoli nel suo cammino, il risultato convenzionale restituito dalla funzione è; indice=0, distanza=1e20.
Come prima prova aggiungiamo una funzione semplificata di disegno della scena:
Il codice principale, con la creazione della scena (4 sfere), e la visuzalizzazione dell'immagine prodotta (in questo caso uso il modulo matplotlib, ma si possono usare anche altri moduli):
risultato dell'elaborazione;
fine terza parte
Aggiungiamo una funzione che restituisce la distanza tra l`origine di ciascun raggio e l`eventuale oggetto incontrato (contestualmente viene restituito anche l`indice dello stesso oggetto). Se il raggio non incontra ostacoli nel suo cammino, il risultato convenzionale restituito dalla funzione è; indice=0, distanza=1e20.
Code:
def distanze(o,r,scena):
t=np.zeros(o.shape[1:])+1e20
ind=np.zeros(t.shape).astype(int)
for i in scena:
i.intercetta(o,r,t,ind)
return t,ind
Come prima prova aggiungiamo una funzione semplificata di disegno della scena:
Code:
def disegna(o_camera,r_camera,scena,luce):
t,ind=distanze(o_camera,r_camera,scena)
img=np.zeros((t.shape))
visibile=(ind>0)
img[visibile]=ind[visibile]
return img
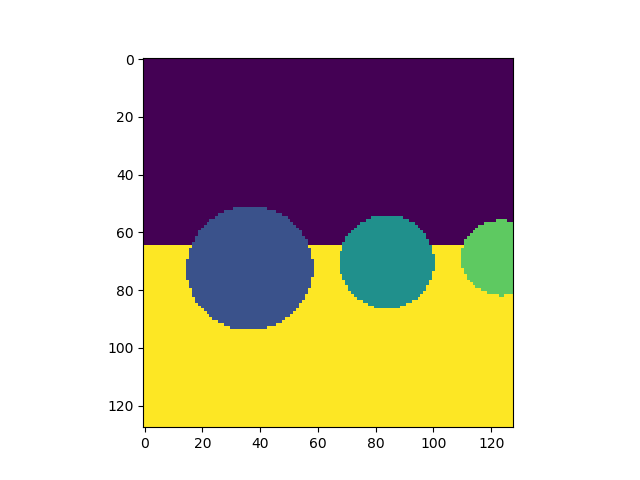
Il codice principale, con la creazione della scena (4 sfere), e la visuzalizzazione dell'immagine prodotta (in questo caso uso il modulo matplotlib, ma si possono usare anche altri moduli):
Code:
luce=normalizza(np.array([0, 5, 10]).reshape(3,1))
scena=[Sfera([.75,.1,1.],.6,[1.0,1.0,1.0]),
Sfera([-.75,.1,2.25],.6,[1.0,1.0,1.0]),
Sfera([-2.75,.1,3.5],.6,[1.0,1.0,1.0]),
Sfera([0,-99999.5,0],99999.,[1.0,1.0,1.0])]
Sfera.C=Sfera.C.reshape(-1,3)
Sfera.R=np.array(Sfera.R)
img=disegna(cam.o,cam.r,scena,luce)
from matplotlib import pyplot as plt
plt.imshow(img.reshape((risoluzione,risoluzione)))
plt.show()
risultato dell'elaborazione;
fine terza parte
Si prega Accesso a partecipare alla conversazione.
- doktorenko
-
 Autore della discussione
Autore della discussione
- Offline
- Utente
-

Less
Di più
- Messaggi: 169
- Ringraziamenti ricevuti 8
5 Anni 6 Mesi fa - 5 Anni 6 Mesi fa #39783
da doktorenko
Risposta da doktorenko al topic Analisi lunari mediante strumenti informatici
Nella quarta parte scriviamo la funzione che calcola la luminosità del suolo lunare (il cuore del programma). Per semplicità, usiamo i valori precalcolati da Scevcenco; eccoli in forma di immagine 16 bit, formato png:
(se vedete un'immagine completamente nera non preoccupatevi)
La codice è questo:
Lo schema di funzionamento:
in entrata la funzione richiede 3 versori:
N) normale al piano p colpito dalla luce nel punto P
L) versore con origine P che punta la fonte di luce
R) versore con origine P che punta verso una determinata cella del sensore
vengono in seguito calcolati:
angolo phi := angolo tra le proiezioni di L e R sul piano p
angolo th_r := angolo tra R e N
angolo th_l := angolo tra L e N
e finalmente si recuperano i valori di luminosità per questi stessi angoli dalla tabella elaborata da Sc.
Prima di terminare, controlliamo se la tabella è stata ricavata con successo dall'immagine png allegata in precedenza; scriviamo questo piccolo programma di verifica:
risultato:
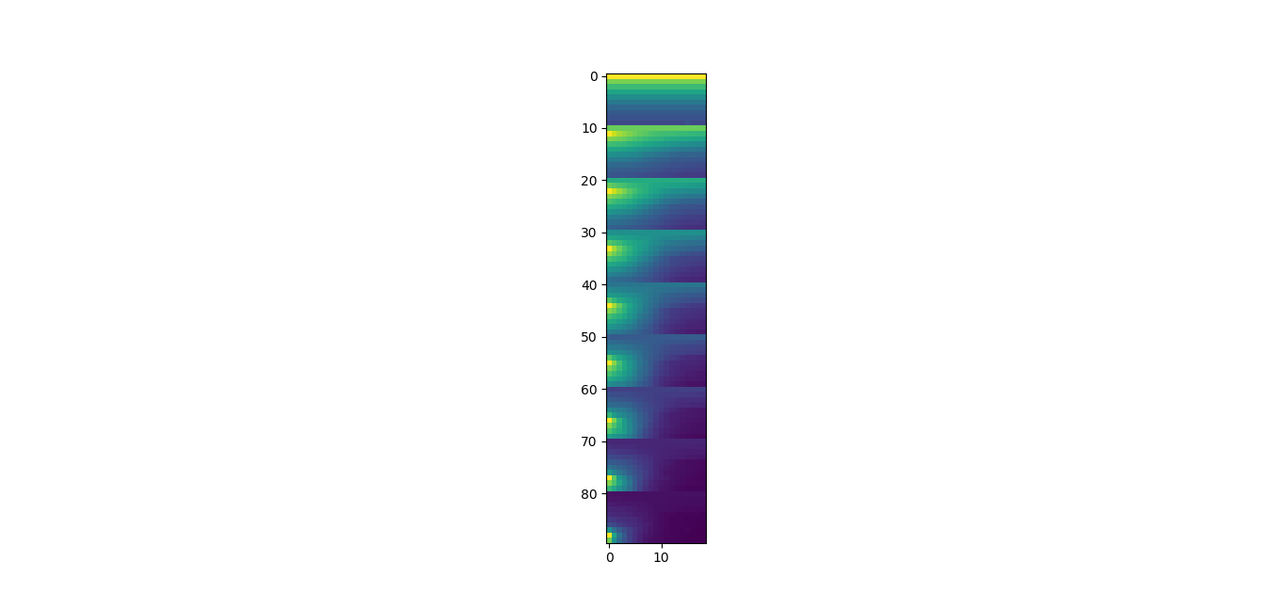
fine quarta parte (nella quinta parte useremo la funzione su oggetti tridimensionali, per simulare il suolo lunare)
(se vedete un'immagine completamente nera non preoccupatevi)
La codice è questo:
Code:
def scev(N,L,R):
NL=prodottoS(N,L)
NR=prodottoS(N,-R)
phi_l=normalizza(L-NL*N)
phi_r=normalizza(-R-NR*N)
cos_phi=prodottoS(phi_l,phi_r)
phi=(np.degrees(np.arccos(cos_phi))/10).astype(int)
thr=(np.degrees(np.arccos(NR))/10).astype(int)
thl=(np.degrees(np.arccos(NL))/10).astype(int)
lum=TAB[thl,thr,phi]
return lum
Lo schema di funzionamento:
in entrata la funzione richiede 3 versori:
N) normale al piano p colpito dalla luce nel punto P
L) versore con origine P che punta la fonte di luce
R) versore con origine P che punta verso una determinata cella del sensore
vengono in seguito calcolati:
angolo phi := angolo tra le proiezioni di L e R sul piano p
angolo th_r := angolo tra R e N
angolo th_l := angolo tra L e N
e finalmente si recuperano i valori di luminosità per questi stessi angoli dalla tabella elaborata da Sc.
Prima di terminare, controlliamo se la tabella è stata ricavata con successo dall'immagine png allegata in precedenza; scriviamo questo piccolo programma di verifica:
Code:
from matplotlib import pyplot as plt
b=plt.imread("scevcenco.png")*65.535
plt.imshow(b)
plt.show()
risultato:

fine quarta parte (nella quinta parte useremo la funzione su oggetti tridimensionali, per simulare il suolo lunare)
Ultima Modifica 5 Anni 6 Mesi fa da doktorenko. Motivo: codice più compatto; corrette didascalie
Si prega Accesso a partecipare alla conversazione.
- doktorenko
-
 Autore della discussione
Autore della discussione
- Offline
- Utente
-

Less
Di più
- Messaggi: 169
- Ringraziamenti ricevuti 8
5 Anni 6 Mesi fa - 5 Anni 6 Mesi fa #39810
da doktorenko
Risposta da doktorenko al topic Analisi lunari mediante strumenti informatici
Nella quinta parte modifichiamo la funzione che disegna gli oggetti in modo da aggiungere ombre e riflessi; innanzitutto inseriamo una funzione per il calcolo delle coordinate dei punti raggiunti dai raggi uscenti dalla camera:
poi una funzione che calcola la riflessione prodotta da una superficie lucidata a specchio:
raggio_uscente = normalizza(raggio_incidente - normale_superficie * 2 (raggio_incidente x normale_superficie) )
due pseudo funzioni per sintetizzare il codice:
Calcoliamo ora le distanze raggi_camera - oggetti visibili:
creiamo tre indici:
1) oggetti := tutti i raggi che colpiscono un oggetto nell`inquadratura
2) regolite := sfera #4, materiale Scev. (sottoinsieme di 1)
3) riflettenti := altre sfere (sottoinsieme di 1)
calcoliamo ora le coordinate 3d di ogni punto raggiunto (indice 1), e la normale alla superficie in quello stesso punto:
cambiamo la direzione ai raggi che raggiungono superfici riflettenti (indice #3):
calcoliamo la distanza tra l'origine di questi nuovi raggi (punto di rimbalzo) e le eventuali superfici toccate:
di questi nuovi raggi, raggruppiamo in un nuovo indice tutti quelli che toccano la superficie lunare (indice #4 := regolite_riflessa):
calcoliamo le coordinate (e le normali) dei punti toccati:
raggruppiamo gli indici #4 e #2 in un unico indice (tutta la regolite inquadrata direttamente e di riflesso):
da questo ultimo gruppo di punti, facciamo partire dei raggi in direzione della fonte di luce:
eliminiamo dal gruppo tutti i punti in ombra (sono i punti dai quali partono i raggi che incontrano un ostacolo)
calcoliamo finalmente la luminosità dei punti rimanenti secondo la nostra tabella precalcolata:
riscriviamo il codice principale:
risultato (in falsi colori):
fine quinta parte (nel prossimo messagiio invio il listato unito)
Code:
def disegna(O,R,scena,l):
Pxyz = lambda i: O[:,i]+t[i]*R[:,i]# xyz_punto = xyz_origine_raggio + distanza * direzione_raggio
poi una funzione che calcola la riflessione prodotta da una superficie lucidata a specchio:
Code:
riflesso = lambda i : normalizza(R[:,i]-N[:,i]*2*prodottoS(R[:,i],N[:,i]))
raggio_uscente = normalizza(raggio_incidente - normale_superficie * 2 (raggio_incidente x normale_superficie) )
due pseudo funzioni per sintetizzare il codice:
Code:
distanza = lambda i : distanze(O[:,i]+N[:,i]*0.00001,R[:,i],scena)
normale = lambda i : normalizza(O[:,i]-Sfera.C[ind[i]].T)
Calcoliamo ora le distanze raggi_camera - oggetti visibili:
Code:
img=np.zeros((R.shape[1:]))
N=np.zeros((R.shape))
t,ind=distanze(O,R,scena)
creiamo tre indici:
1) oggetti := tutti i raggi che colpiscono un oggetto nell`inquadratura
2) regolite := sfera #4, materiale Scev. (sottoinsieme di 1)
3) riflettenti := altre sfere (sottoinsieme di 1)
Code:
oggetti=np.where(ind!=0)[0]
regolite=oggetti[(ind[oggetti]==4)]
riflettenti=oggetti[ind[oggetti]!=4]
calcoliamo ora le coordinate 3d di ogni punto raggiunto (indice 1), e la normale alla superficie in quello stesso punto:
Code:
O[:,oggetti]=Pxyz(oggetti)
N[:,oggetti]=normalizza(O[:,oggetti]-Sfera.C[ind[oggetti]].T)
cambiamo la direzione ai raggi che raggiungono superfici riflettenti (indice #3):
Code:
R[:,riflettenti]=riflesso(riflettenti)
calcoliamo la distanza tra l'origine di questi nuovi raggi (punto di rimbalzo) e le eventuali superfici toccate:
Code:
t[riflettenti],ind[riflettenti]=distanza(riflettenti)
di questi nuovi raggi, raggruppiamo in un nuovo indice tutti quelli che toccano la superficie lunare (indice #4 := regolite_riflessa):
Code:
regolite_riflessa=riflettenti[ind[riflettenti]==4]
calcoliamo le coordinate (e le normali) dei punti toccati:
Code:
O[:,regolite_riflessa]=Pxyz(regolite_riflessa)
N[:,regolite_riflessa]=normale(regolite_riflessa)
raggruppiamo gli indici #4 e #2 in un unico indice (tutta la regolite inquadrata direttamente e di riflesso):
Code:
regolite=np.concatenate((regolite,regolite_riflessa))
da questo ultimo gruppo di punti, facciamo partire dei raggi in direzione della fonte di luce:
Code:
t[regolite],ind[regolite]=distanze(O[:,regolite]+N[:,regolite]*0.00001,l,scena)
eliminiamo dal gruppo tutti i punti in ombra (sono i punti dai quali partono i raggi che incontrano un ostacolo)
Code:
regolite=regolite[ind[regolite]==0]
calcoliamo finalmente la luminosità dei punti rimanenti secondo la nostra tabella precalcolata:
Code:
img[regolite]=scev(N[:,regolite],l,R[:,regolite])
return img
riscriviamo il codice principale:
Code:
from matplotlib import pyplot as plt
risoluzione=512*2
cam=Camera([0,.35,-3],risoluzione)
luce=normalizza(np.array([0, 5, 10]).reshape(3,1))
scena=[Sfera([.75,.1,1.],.6,[1.0,1.0,1.0]),
Sfera([-.75,.1,2.25],.6,[1.0,1.0,1.0]),
Sfera([-2.75,.1,3.5],.6,[1.0,1.0,1.0]),
Sfera([0,-99999.5,0],99999.,[1.0,1.0,1.0])]
Sfera.C=Sfera.C.reshape(-1,3)
Sfera.R=np.array(Sfera.R)
TAB=(plt.imread("scevcenco.png")*65.535).reshape((9,10,19))
img=disegna(cam.o,cam.r,scena,luce)
plt.imshow(img.reshape((risoluzione,risoluzione)))
plt.show()
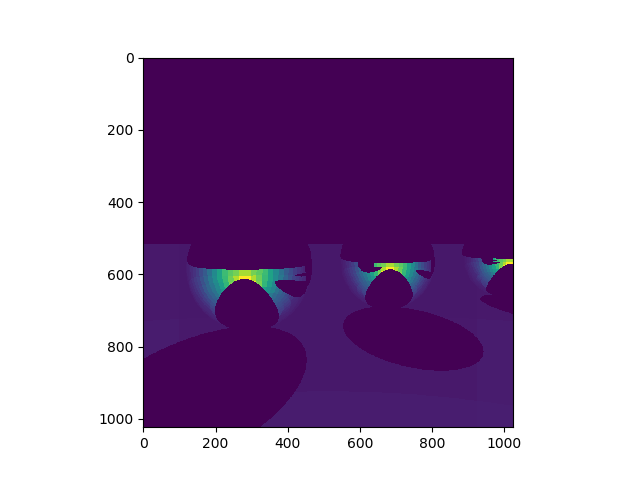
risultato (in falsi colori):
fine quinta parte (nel prossimo messagiio invio il listato unito)
Ultima Modifica 5 Anni 6 Mesi fa da doktorenko. Motivo: correzione codice
Si prega Accesso a partecipare alla conversazione.
- doktorenko
-
 Autore della discussione
Autore della discussione
- Offline
- Utente
-

Less
Di più
- Messaggi: 169
- Ringraziamenti ricevuti 8
5 Anni 6 Mesi fa #39871
da doktorenko
Risposta da doktorenko al topic Analisi lunari mediante strumenti informatici
Codice riunito (e ottimizzato):
Code:
import numpy as np
def prodottoS(a,b):
if (b.ndim==1):
return a.dot(b)
else:
return np.einsum("ij,ij->i",a,b)
def normalizza(a):
if (a.ndim==1):
return a/np.linalg.norm(a,axis=0)
else:
return a/np.expand_dims(np.sqrt(prodottoS(a,a)),axis=1)
class Camera:
def __init__(self,centro,risoluzione):
global o
self.c=np.array(centro)
F=.61
mm=.55
xv,yv=np.meshgrid(np.linspace(-.5,.5,risoluzione),
np.linspace(-.5,.5,risoluzione))
zv=np.zeros((risoluzione,risoluzione))-F
o=np.dstack((xv*mm,yv*mm,zv)).reshape(-1,3)
self.r=-normalizza(o)
self.o=(o+self.c)
class Sfera:
C=0
R=[]
n=1
def __init__(self,centro,raggio,colore):
if (self.n==1):
Sfera.C=np.array(centro)
self.c=np.array(centro)
self.r=raggio
Sfera.C=np.concatenate((Sfera.C,self.c))
Sfera.R.append(raggio)
self.r2=raggio*raggio
self.col=np.array(colore)
self.i=Sfera.n
Sfera.n+=1
def intercetta(self,origine,direzione,d0,ind):
L=self.c-origine
np.seterr(all='ignore')
tca=prodottoS(L,direzione)
d2= prodottoS(L,L)-tca*tca
thc=np.sqrt(self.r2-d2)
t0=tca-thc
t1=tca+thc
t0=np.where(t1<t0,t1,t0)
t0=np.where(t0<0,np.nan,t0)
m=np.where(t0<d0)
d0[m]=t0[m]
ind[m]=self.i
np.seterr(all='warn')
def distanze(o,r,scena):
t=np.zeros(o.shape[:-1])+1e20
ind=np.zeros(t.shape).astype(int)
for i in scena:
i.intercetta(o,r,t,ind)
return t,ind
def disegna(O,R,scena,l):
Pxyz = lambda i: O[i]+R[i]*t[i,np.newaxis]
riflesso = lambda i : normalizza( R[i]-(N[i]*2*prodottoS(R[i],N[i])[:,np.newaxis]))
distanza = lambda i : distanze(O[i]+N[i]*0.00001,R[i],scena)
normale = lambda i : normalizza(O[i]-Sfera.C[ind[i]])
img=np.zeros((R.shape[:-1]))
N=np.zeros((R.shape))
t,ind=distanze(O,R,scena)
oggetti=np.where(ind!=0)[0]
regolite=oggetti[(ind[oggetti]==4)]
riflettenti=oggetti[ind[oggetti]!=4]
O[oggetti]=Pxyz(oggetti)
N[oggetti]=normalizza(O[oggetti]-Sfera.C[ind[oggetti]])
R[riflettenti]=riflesso(riflettenti)
t[riflettenti],ind[riflettenti]=distanza(riflettenti)
regolite_riflessa=riflettenti[ind[riflettenti]==4]
O[regolite_riflessa]=Pxyz(regolite_riflessa)
N[regolite_riflessa]=normale(regolite_riflessa)
regolite=np.concatenate((regolite,regolite_riflessa))
t[regolite],ind[regolite]=distanze(O[regolite]+N[regolite]*0.00001,l,scena)
regolite=regolite[ind[regolite]==0]
img[regolite]=scev(N[regolite],l,R[regolite])
return img
def scev(N,L,R):
NL=prodottoS(N,L)
NR=prodottoS(N,-R)
phi_l=normalizza(L-N*NL[:,np.newaxis])
phi_r=normalizza(-R-N*NR[:,np.newaxis])
cos_phi=prodottoS(phi_l,phi_r)
phi=(np.degrees(np.arccos(cos_phi))/10).astype(int)
thr=(np.degrees(np.arccos(NR))/10).astype(int)
thl=(np.degrees(np.arccos(NL))/10).astype(int)
return TAB[thl,thr,phi]
from matplotlib import pyplot as plt
import time
risoluzione=512*2
cam=Camera([0,.35,-3],risoluzione)
luce=np.array([0, 5, 10])
luce=normalizza(luce)
scena=[Sfera([.75,.1,1.],.6,[1.0,1.0,1.0]),
Sfera([-.75,.1,2.25],.6,[1.0,1.0,1.0]),
Sfera([-2.75,.1,3.5],.6,[1.0,1.0,1.0]),
Sfera([0,-99999.5,0],99999.,[1.0,1.0,1.0])]
Sfera.C=Sfera.C.reshape(-1,3)
Sfera.R=np.array(Sfera.R)
TAB=(plt.imread("scevcenco.png")*65.535).reshape((9,10,19))
t0=time.time()
img=disegna(cam.o,cam.r,scena,luce)
print (time.time()-t0)
plt.imshow(img.reshape((risoluzione,risoluzione)))
plt.show()
Si prega Accesso a partecipare alla conversazione.
- doktorenko
-
 Autore della discussione
Autore della discussione
- Offline
- Utente
-

Less
Di più
- Messaggi: 169
- Ringraziamenti ricevuti 8
5 Anni 6 Mesi fa #39924
da doktorenko
Risposta da doktorenko al topic Analisi lunari mediante strumenti informatici
Per una simulazione piu` corrispondente con la scena originale, dobbiamo pero` cambiare il materiale della sfera (ora e` completamente riflettente).
Aggiungiamo quindi tre nuove funzioni:
La funzione emisfero individua dei punti sulla superficie di una semisfera unitaria, distribuiti secondo la sequenza di Hammersley e secondo il coseno dell`angolo th (piu` punti sull`unico polo); la funzione nuovoSdC crea un nuovo sistema di coordinate ortogonali in 3 dimensioni: sistema che avra` il versore N, argomento della funzione, come asse Y; la funzione inverti32bit crea la sequenza Van der Corput (parte della seq. di H.).
Modifichiamo la parte finale della funzione disegna:
Modifichiamo il codice principale: abbassiamo la risoluzione; creiamo i nostri punti sulla semisfera; aggiungiamo la variabile globale CAMPIONI (numero di punti sulla s.):
Con queste modifiche:
1) un raggio della camera che colpisce un punto P della superficie del nuovo materiale
2) viene moltiplicato e diffuso da quello stesso punto nelle direzioni individuate dai punti della semisfera creata in precedenza (semisfera orientata secondo la normale al punto P)
3) la luminosita` del punto P viene quindi calcolata come somma di tutti i contributi dei raggi lanciati da quel punto, in base alla luminosita` della superficie che andranno a toccare
In realta` il punto 3) non e` ancora sviluppato: come prima prova, invece della luminosita`, abbiamo calcolato la distanza media del punto P dagli altri oggetti sulla scena; ecco infatti il risultato delle modifiche:
(Il punto 3 non l`ho ancora programmato: non so neanch`io quale potra` essere il risultato )
)
Aggiungiamo quindi tre nuove funzioni:
Code:
def inverti32bit(bits):
bits = (bits << 16) | (bits >> 16);
bits = ((bits & 0x55555555) << 1) | ((bits & 0xAAAAAAAA) >> 1);
bits = ((bits & 0x33333333) << 2) | ((bits & 0xCCCCCCCC) >> 2);
bits = ((bits & 0x0F0F0F0F) << 4) | ((bits & 0xF0F0F0F0) >> 4);
bits = ((bits & 0x00FF00FF) << 8) | ((bits & 0xFF00FF00) >> 8);
return bits * 2.3283064365386963e-10
def emisfero(n=128):
N=np.arange(n,dtype=np.uint32)
u=inverti32bit(N)
theta=np.arccos(np.sqrt(1-u))
v=N/n
phi=2*np.pi*v
x = np.sin(theta)*np.cos(phi)
z = np.sin(theta)*np.sin(phi)
y = np.cos(theta)
return np.dstack((x,y,z))[0]
def nuovoSdC(N):
Nt=np.zeros(N.shape)
Nb=np.zeros(N.shape)
m=np.abs(N[:,0])>np.abs(N[:,1])
if len(Nt[m]):
Nt[m]=np.dstack((N[m][:,2],np.zeros(m.sum()),-N[m][:,0]))[0]
if len(Nt[~m]):
Nt[~m]=np.dstack((np.zeros((~m).sum()),-N[~m][:,2],N[~m][:,1]))[0]
Nt=normalizza(Nt)
Nb=np.cross(N,Nt)
return Nb,Nt
La funzione emisfero individua dei punti sulla superficie di una semisfera unitaria, distribuiti secondo la sequenza di Hammersley e secondo il coseno dell`angolo th (piu` punti sull`unico polo); la funzione nuovoSdC crea un nuovo sistema di coordinate ortogonali in 3 dimensioni: sistema che avra` il versore N, argomento della funzione, come asse Y; la funzione inverti32bit crea la sequenza Van der Corput (parte della seq. di H.).
Modifichiamo la parte finale della funzione disegna:
Code:
....
O[oggetti]=Pxyz(oggetti)
N[oggetti]=normalizza(O[oggetti]-Sfera.C[ind[oggetti]])
##la parte da cambiare e` la seguente:
Nt,Nb=nuovoSdC(N[oggetti])
m=np.dstack((Nt,N[oggetti],Nb))
Re=np.inner(EMI,m)
Re=np.swapaxes(Re,0,1).reshape(-1,3)
Oe=np.repeat(O[oggetti]+N[oggetti]*0.00001,CAMPIONI,axis=0)
t0,ind0=distanze(Oe,Re,scena)
t0=t0.reshape(-1,CAMPIONI).sum(1)
img[oggetti]=t0
return img
Modifichiamo il codice principale: abbassiamo la risoluzione; creiamo i nostri punti sulla semisfera; aggiungiamo la variabile globale CAMPIONI (numero di punti sulla s.):
Code:
from matplotlib import pyplot as plt
import time
##parte da modificare:
CAMPIONI=128
EMI=emisfero(CAMPIONI)
risoluzione=128
##fine modifica
cam=Camera([0,.35,-3],risoluzione)
Con queste modifiche:
1) un raggio della camera che colpisce un punto P della superficie del nuovo materiale
2) viene moltiplicato e diffuso da quello stesso punto nelle direzioni individuate dai punti della semisfera creata in precedenza (semisfera orientata secondo la normale al punto P)
3) la luminosita` del punto P viene quindi calcolata come somma di tutti i contributi dei raggi lanciati da quel punto, in base alla luminosita` della superficie che andranno a toccare
In realta` il punto 3) non e` ancora sviluppato: come prima prova, invece della luminosita`, abbiamo calcolato la distanza media del punto P dagli altri oggetti sulla scena; ecco infatti il risultato delle modifiche:
(Il punto 3 non l`ho ancora programmato: non so neanch`io quale potra` essere il risultato
Si prega Accesso a partecipare alla conversazione.
- doktorenko
-
 Autore della discussione
Autore della discussione
- Offline
- Utente
-

Less
Di più
- Messaggi: 169
- Ringraziamenti ricevuti 8
5 Anni 6 Mesi fa #39970
da doktorenko
Risposta da doktorenko al topic Analisi lunari mediante strumenti informatici
Completiamo il punto 3 (vedi messaggio precedente); cambiamo le funzioni di utilita` in modo che possano accettare una dimensione aggiuntiva (il numero dei campioni):
modifichiamo la funzione distanze (per lo stesso motivo):
riscriviamo la funzione disegna:
commento alcune variabili:
R[sfere] := tutti i raggi uscenti dalla camera che colpiscono le sfere nei punti Pe
Re := le direzioni dei raggi che da ciascun punto Pe si diffondono a semisfera
ireg := l`indice di quei raggi che dopo il rimbalzo incontrano il suolo illuminato
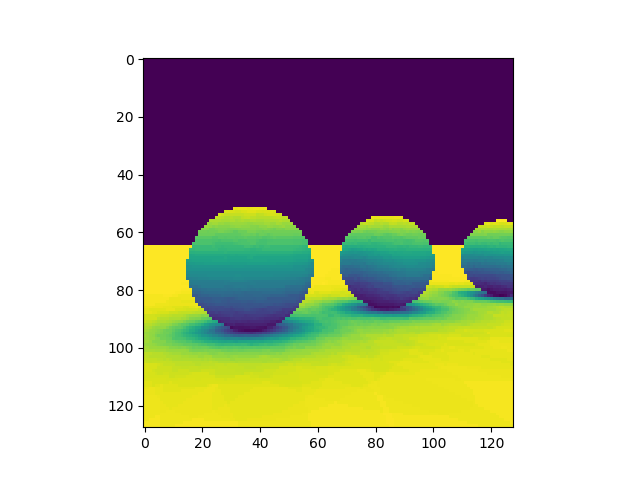
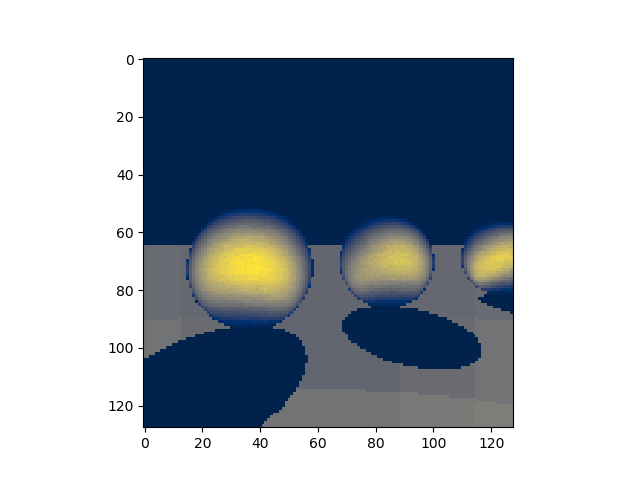
risultato:
(in falsi colori; 128x128; 512 campioni)
Code:
def prodottoS(a,b):
if (b.ndim==1):
return a.dot(b)
elif(a.ndim==2 and b.ndim==2):
return np.einsum("ij,ij->i",a,b)
elif(a.ndim==3 and b.ndim==3):
return np.einsum("ijk,ijk->ij",b,a)
elif(a.ndim==2 and b.ndim==3):
return np.einsum("ijk,jk->ij",b,a)
def normalizza(a):
if (a.ndim==1):
return a/np.linalg.norm(a,axis=0)
if (a.ndim==2):
return a/np.expand_dims(np.sqrt(prodottoS(a,a)),axis=1)
elif (a.ndim==3):
return a/np.expand_dims(np.sqrt(prodottoS(a,a)),axis=2)
modifichiamo la funzione distanze (per lo stesso motivo):
Code:
def distanze(o,r,scena):
if (r.ndim==1):
t=np.zeros(o.shape[:-1])+1e20
else:
t=np.zeros(r.shape[:-1])+1e20
ind=np.zeros(t.shape,dtype=np.uint8)
for i in scena:
i.intercetta(o,r,t,ind)
return t,ind
riscriviamo la funzione disegna:
Code:
def disegna(O,R,scena,l):
Pxyz = lambda i: O[i]+R[i]*t[i,np.newaxis]
riflesso = lambda i : normalizza( R[i]-(N[i]*2*prodottoS(R[i],N[i])[:,np.newaxis]))
distanza = lambda i : distanze(O[i]+N[i]*0.00001,R[i],scena)
normale = lambda i : normalizza(O[i]-Sfera.C[ind[i]])
img=np.zeros((R.shape[:-1]))
N=np.zeros((R.shape))
t,ind=distanze(O,R,scena)
oggetti=np.where(ind!=0)[0]
regolite=oggetti[(ind[oggetti]==4)]
sfere=oggetti[ind[oggetti]!=4]
O[oggetti]=Pxyz(oggetti)
N[oggetti]=normalizza(O[oggetti]-Sfera.C[ind[oggetti]])
Nt,Nb=nuovoSdC(N[sfere])
m=np.dstack((Nt,N[sfere],Nb))
Re=np.inner(EMI,m)
Oe=O[sfere]
t0,ind0=distanze(Oe,Re,scena)
Pe=Oe+Re*t0[...,np.newaxis]
Ne=normalizza(Oe-Sfera.C[ind0])
t1,ind1=distanze(Pe+Ne*0.00001,l,scena)
ireg=(ind0==4)*(ind1==0)
reg=np.zeros(ireg.shape)
reg[ireg]=scev(Ne[ireg],l,Re[ireg])
img[sfere]=np.average(reg,axis=0)*prodottoS(N[sfere],-R[sfere])*.9
t[regolite],ind[regolite]=distanze(O[regolite]+N[regolite]*0.00001,l,scena)
regolite=regolite[ind[regolite]==0]
img[regolite]=scev(N[regolite],l,R[regolite])
return img
commento alcune variabili:
R[sfere] := tutti i raggi uscenti dalla camera che colpiscono le sfere nei punti Pe
Re := le direzioni dei raggi che da ciascun punto Pe si diffondono a semisfera
ireg := l`indice di quei raggi che dopo il rimbalzo incontrano il suolo illuminato
risultato:
(in falsi colori; 128x128; 512 campioni)
Si prega Accesso a partecipare alla conversazione.
Tempo creazione pagina: 0.331 secondi